信号抽样(卷名：电工)
sampling of signals
在某些选定的时刻抽取连续时间信号在各该时刻的值。数字计算机所处理的信号必须是离散时间信号。在涉及连续时间信号时，就必须先以适当的频度从中抽取其在各时刻的数值，形成相应的离散时间信号，然后进行处理。
连续时间信号的抽样 抽样的示意如图1所示。
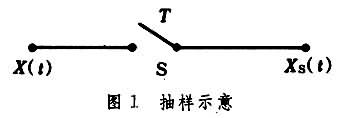图中X(t)为被抽样的连续时间信号，XS(t)是抽样后的信号，S是一个开关。当S闭合时，XS(t)就等于X(t)在该瞬刻的值；S断开时，XS(t)等于零。S每隔时间T 闭合一次，每次闭合的时间τ很短，可以认为τ接近于零。T为抽样的时间间隔。如果相邻的抽样时间间隔相等，即T 为常数，那就是均匀抽样。1/T 称为抽样频率，以fS表示，fS＝1/T；或用ΩS表示，ΩS＝2π/T。均匀抽样是一种广泛使用的抽样形式。它可表示为
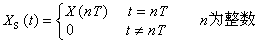式中X(nT)为t=nT时X(t)的值。均匀抽样还可以是用连续时间函数X(t)对一冲激序列进行的脉冲幅度调制。设冲激序列P(t)为一串单位冲激，而相邻冲激的时间间隔为T，则
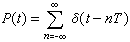于是
抽样信号 XS(t)是用X(t)与单位冲激序列P(t)相乘的结果。抽样保持 由于连续时间信号的抽样值经过量化、编码而变换成数字量需要一定的时间，所以信号抽样后要保持一段时间。抽样与保持常常结合在一起，称为信号的抽样与保持。抽样和保持的具体方法如图2所示。
图中A1、A2是两个接成电压跟随器的运算放大器，当控制脉冲为高电平时，电子开关导通，电容C被迅速充电，其电压等于该时刻的信号电压X（t）；随即经过很短的时间τ后，电子开关受V 的低电平控制而断开，此时电容电压保持不变。经过时间TS后再重复上述过程。抽样保持器的输出电压X▂(t)为台阶形状。抽样定理 一信号在时域中用一时间函数X(t)表示，在频域中用其频率函数X(jΩ)表示。X(t)与X(jΩ)为一个傅里叶变换对。C.E.香农等人在1948年提出的抽样定理说明了X(t)的抽样序列X(nT)与X(t)的关系。定理揭示：设X(t)是一频带宽度有限的信号，即当|Ω|＞Ωm时X(jΩ)＝0，则由以大于2Ωm的抽样率ΩS(等于2π/T)进行抽样所得的抽样序列X(nT)可以完全确定X(t)。fS=2Ωm的抽样频率也称为奈奎斯特频率。
抽样定理的意义在于它确定了抽样率必须高于2Ωm才能从抽样序列恢复原来的连续信号。由抽样信号的傅里叶变换知道，抽样信号的傅里叶变换在频域中是以ΩS为周期的连续周期函数。当抽样间隔增大，ΩS降低到不满足大于2Ωm的条件时，则抽样信号XS(t)的傅里叶变换的幅度频谱|X(ejw)|成为图3中粗黑线所示的形状。
这时|X(ejw)|的频谱已不再与|X(jΩ)|的频谱相似。这时(ΩS－Ωm)＜Ωm，以 Ω=0为中心的
X(jΩ)与以Ω=ΩS为中心的|X(jΩ-jΩS)|有一部分混叠在一起，这种现象称为混叠现象。把频域中的连续频率函数X(jΩ)在频域中抽样得到的离散频谱序列XS(jΩ)称为频域采样。
对时限信号X(t)的傅里叶变换X(jΩ)以抽样间隔∮在频域中进行抽样，如选择抽样间隔∮，使
，Tm为X(t)的时限，得到的频域抽样信号XS(j∮)能完全代表X(j∮)，由它能够恢复X(jΩ)或X(t)。