哈密顿正则方程(卷名：物理学)
Hamiltonian canonical equation
经典力学中一组描写系统运动的一阶微分方程组。是W.R.哈密顿于1834年提出的，又称哈密顿方程或正则方程。哈密顿正则方程为
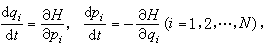
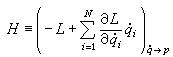
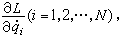解出N 个 妜i为 (E1，E2，…，EN；q1，q2，…，qN；t)的N 个函数，然后代入式(2)就得到哈密顿函数H。对于直角坐标变换到广义坐标的变换式虽然显含时间t，但是动能的表示式不明显地包含t，此时
H＝T2-T0+V，式中T2和T0可说明如下：用(E1，E2，…，EN；q1，q2，…，qN；t)表示的动能式T＝T2+T1+T0，式中T2、T1和T0分别表示广义动量的二次齐次式、一次齐次式和不含广义动量的项。
如果直角坐标变换到广义坐标的变换式不显含t，势函数V也不显含t，则
T＝T2，H＝T+V。即对于保守系统，哈密顿函数是系统总机械能用广义动量表示的公式。
正则方程式(1)是2N个一阶微分方程组，而拉格朗日方程是N个二阶微分方程组，都只适用于完整系统（见约束）的动力学方程组。
由于式(1)的左边不再有变数q和p的导数，所以方程(1)成为如下形式的方程组
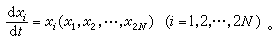
保守系统的正则方程在天体力学和经典统计力学中有重要的应用。在天体力学中从可解的二体问题出发，逐渐添加其他星球的引力，可以把所用的哈密顿函数H，从简单改变成较复杂的 H′。这是天体力学中的摄动法，用来解决考虑太阳和各种行星、卫星的引力作用下的行星运动，由此可制定行星和月球的星历表，在统计力学中的刘维定理就是应用正则方程推导出来的。