CW复形(卷名：数学)
CW complex
一类拓扑空间。重要性在于许多常见的空间属于这一类；另外同伦论的方法对这类空间能较好地发挥。单纯复形（见拓扑学，同调论）是CW复形的特例。粗略地说，CW复形是由一些（有限多个或无穷多个）胞腔从低维到高维逐层堆积而成的空间。同伦论中往往需要在拓扑空间上定义满足某种条件的连续映射。这对非常一般的拓扑空间来说很难着手。但对于CW复形，则可以从低维到高维，在一个一个胞腔上给出定义，即采用“逐层扩张”的方式得到所需要的连续映射。如果扩张到某一层遇到阻碍，就产生阻碍上闭链，阻碍上同调类等等（见同伦论），这样就能利用同调来讨论关于连续映射的扩张或同伦等问题。
设Χ为豪斯多夫空间，{e
}为Χ的一组子空间，α∈Jn(Jn为标号集合），n＝0，1，2，…，记
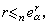
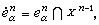
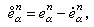并且设下列条件成立：①
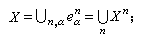
②
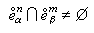蕴涵n＝m，α＝β；③ 对任意一对n，α，有连续映射
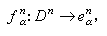满足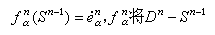
同胚地映为 妏
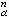，其中Dn为欧氏空间 Rn里的单位球体，Sn-1为 Dn的边界球面。这时称集合 
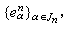n＝0，1，2，…构成空间Χ 的一个胞腔剖分，e
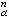（α∈Jn）称为 X 的 n 维胞腔，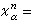
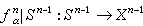称为粘贴映射，Χn称为n维骨架。条件①、②、③蕴涵
具备了一个胞腔剖分的豪斯多夫空间叫作胞腔复形。若
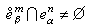，则称e
为e
的一个直接面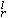。e
称为e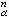
的一个面，如果二者之间可以插入一列有限多个胞腔使得前一个为后一个的直接面。胞腔复形Χ称为CW复形，假如下列条件满足：
C：闭包有限──每个胞腔只有有限多个面；
W：弱拓扑──子集S嶅Χ 为闭集当而且仅当对一切n，α，S∩e
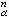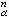为e中的闭集。例如，在球面Sn中，任取一点p∈Sn，令e0=p，en=Sn，则Sn剖分成了只含两个胞腔{e0，en}的胞腔复形。
又如，在实射影空间RPn中，有一个由n+1个胞腔e0，e1，…，en构成的胞腔剖分，亦即每个维数恰好有一个胞腔。
上面已经提到，CW复形Χ可看作是逐层粘贴胞腔而得到的：Χ0为若干个点；设Χn-1已粘好，用粘贴映射x
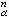将Dn粘贴到Χn-1上得到各个e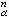，从而造出Χn，……。同一个空间可以有不同的胞腔剖分。一般胞腔剖分比单纯剖分所含有的胞腔总数可以少得多，这是胞腔剖分的一大优点。