代数K理论(卷名：数学)
algebraic K-theory
产生于20世纪60年代初期、在近20年得到蓬勃发展的一个新的代数学分支。人们最初企图推广线性代数中的某些部分，例如将维数理论推广到一般环的模上，而发展出由环范畴到阿贝尔群范畴的一系列函子，这些函子以记号K0，K1，…来表示，研究这些函子的理论，就称为代数K 理论。
和拓扑K 理论一样，代数K 理论也起源于A.格罗腾迪克在1957年给出的广义黎曼-罗赫定理的工作，在其定理的证明中第一次出现了在一个概型 X上的向量丛的格罗腾迪克群K(X)。如果取X=Spec(A)（A的谱）是仿射的，这里A是可换环，那么X上的向量丛范畴等价于有限生成投射A模的范畴P(A)。由此，对任意环A（指含有单位元的结合环，不一定可换），可定义范畴P(A)的格罗腾迪克群，以K0(A)表示。
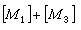，若
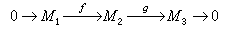在范畴P(A)中是正合序列。例如，环A=F是一个域时，K0(F)≌Z，这里Z是整数加法群。又如，环A是数域F的代数整数环，
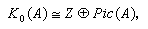其中Pic(A)表示 A 的皮卡群，这里它同构于A的理想类群C(A)。对任意交换环A的皮卡群，是指由rank1的有限生成投射A模的同构类相对张量积圱运算形成的群。如果
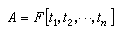是域F上的多项式环，那么任一有限生成投射A 模是自由的，这就是著名的塞尔猜想。在解决这一著名猜想过程中，启发和派生出很多代数 K 理论的工作。令
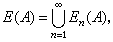这里 Kn(A)是由 GLn(A)中初等矩阵eij(λ)(i≠j， λ∈A)全体生成的子群，有K(A)=[GL(A)，GL(A)]。于是K1(A)＝GL(A)/K(A)。实际上，对任何一个阿贝尔范畴的相容子范畴b都可以给出按格罗腾迪克方式定义的怀特海群，用K1b表示，其具体构造如下：首先由 b构造新范畴愋，Obj愋=｛(M，α)│M∈b，α是M的自同构｝。所谓 ƒ∈Hom((M，α)，(M′，α′))，是指 ƒ∈Hom(M，M′)和使得ƒ。α＝α′。ƒ。如果序列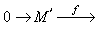
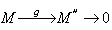在b中是正合的，那么序列
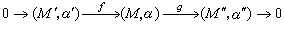(*)在愋中称为正合的。K1愋是一个阿贝尔群， 生成元集合是{[M，α]│(M，α)∈Obj愋}，如果序列(*)在愋中是正合的，那么有定义关系：[M，α]=[M′，α′]+[M″，α″]；如果α、β都是M的自同构，那么有定义关系:[M，αβ]=[M，α]+[M，β]。H.巴斯给出了如下的结果：
从K1(A)到K1P(A)存在一个自然同构φ:K1(A)=GL(A)/K(A)→K1P(A)，它由φ([α])=[An，α] 给出，其中α∈GLn(A)，[α]∈GL(A)/K(A)。
若环 A是交换的，令 SK1(A)＝SL(A)／K(A)，其中
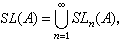则有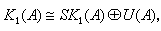
这里U(A)是环A中所有可逆元全体构成的乘法群。若A是一个域或局部环，有SK1(A)=0，这时K1(A)≌U(A)。关于洛朗多项式环A[t，t-1]上的群K1(A[t，t-1])的结构被看作“古典”代数K 理论的柱石。这里A是一个环，t 是超越元，t可与A的元素交换，A[t，t-1]由洛朗多项式
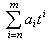组成，其中n≤m；n、m∈Z。H.巴斯等人给出:对任何环A，存在一个自然分裂的正合序列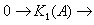 
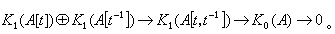由此可得
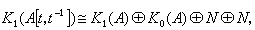其中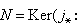
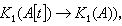j:A[t]→A，j(t)=1。这一结果给出了函子K0和K1之间的深刻关系，也启发了对函子K-n(n>0)的定义。对于n>0，阿贝尔群K-n(A)用下面的公式给出归纳的定义：
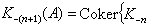
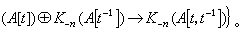其中余核 Coker(ƒ:A→B)=B/ƒ(A)。几个例子：如果A=F是一个域，
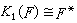（F 的乘法群）；K1(Z)≌{±1}乘法群；K1(Z[i])≌{±1，±i}乘法群，其中i2=-1。
；
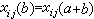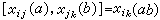，i≠k;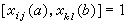
，j≠k，i≠l。由群Str(A)到群GLr(A)的同态
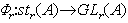，由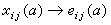 
给出。Kerφr定义为 K2(r，A)，即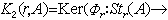
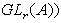。令r→
，得到同态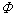
:St(A)→GL(A)，从而得到正合序列0→Ker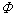→St(A)→GL(A)→K1(A)→0。定义K2(A)为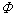的核，即 K2(A)=Ker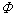。米尔诺指出，K2(A)就是St(A)的中心，所以是阿贝尔群。D.G.奎伦于1970年给出高次K群（指n≥3）的定义，并提供了第一个计算高次K 群的有效工具。他精确地计算了群Kx(Fq)（Fq是q元有限域），
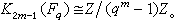
对不同类型的环A，群Kn(A)在数学的许多领域中有重要的应用。例如:在拓扑K 理论中，当取A=C(X)是紧空间X上的连续复值函数环时，Kn(C(X))与X的复的K 理论有关。在代数几何学中，当取A是仿射代数簇X上多项式函数环时，A 的代数K 理论与X上的代数向量丛和相交理论有关。在数论中，当取A是数域F 的代数整数环时，群Kn(A)和Kn(F)与数论有深刻的联系。在几何拓扑学中，当取A=Zπ 是群π的整数群环时，群Kn(Zπ)与几何拓扑的障碍群有密切关系。
参考书目
H. Bass，Algebraic K-Theory， Benjamin，New York，1968.
J.Milnor，Introduction to Algebraic K-Theory， Annalsof Mathematics Studies，Princeton Univ. Press，Princeton，1971.
H.Bass，Algebraic K-Theory:A Historical Survey，Proceedings of the International Congress of MatheMaticians， Vancouver， 1974.
J.R.Silvester，Introduction to Algebraic K-Theory，Chapman and Hall， London， 1981.