动力学普遍方程(卷名：力学)
general equation of dynamics
又称拉格朗日－达朗伯方程（LagrangedˊAlembert equation），可表达为：质点系中各质点上的主动力
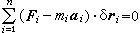。 (1)按照达朗伯原理，对每一质点有：Fi+Ni-mai=0，从而(Fi+Ni-miai)·δri=0，所以其总和 
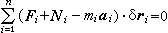。 (2)对理想约束有
，故由式(2)即得式(1)。应用统一坐标，以Xj表示xj方向的主动力，则式(1)可写作：
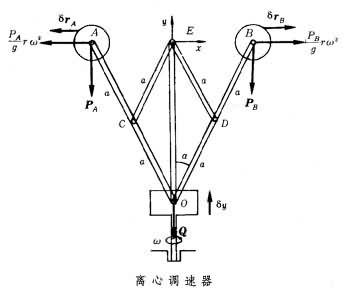
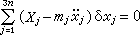。 (3)对于动力学问题，3n个δxj(j=1，2，…，3n)，有约束方程相联系，由式(3)不能得出 Xj-mj塯j=0，只能利用约束方程消去与约束方程个数相等的δx后，才能使留下的δ)xj前的括号为零。例如，在中，重为PA和PB(PA=PB=P)的两球A和B与一重为Q的套管O用杆连接，且OC=AC=EC=OD=DE=DB=a，略去杆重不计，则此机构可看成由三个质点A、B与O组成。令 r＝BE＝AE＝2asinα ，则当机构以角速度ω绕y轴转动时，动力学普遍方程可写为：
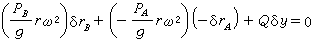或
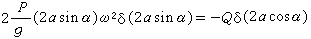，所以有：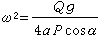 
。