变质量体运动(卷名：力学)
motion of a variable-mass body
变质量体是在运动过程中本身质量发生明显变化的物体，这种物体的运动就是变质量体运动。这里所说的物体质量的变化不是指质量的消灭或产生，而是指在某一瞬时以前或以后，物体中有一部分质量未被考虑在内；前者相当于有质量并入而使物体的质量增加，后者相当于有质量分出而使物体的质量减少。如果变质量体的转动速度和加速度同平动的速度和加速度相比可以忽略不计，则此变质量体可看作一个变质量点。这种情况下的变质量体问题仍属经典力学范畴。
在工程技术和自然界中有许多变质量体的例子：火箭喷出燃料燃烧后的残余物使火箭质量发生变化；喷气飞机是一般情况下的变质量体，它不断吸入空气而使质量增加，但又不断喷出燃气而使质量减少，即质量的并入和分出同时发生；流星体在闯入大气层时，质量由于摩擦燃烧而减少；浮冰由于海水冻结使质量增加，或由于融化而使质量减小；棉纺厂的纱锭在转动过程中也在不断改变质量和转动惯量，等等。
基本运动微分方程 假设变质量质点的并入或分出微粒是连续发生的，而且这种质量的并入或分出是属于微粒和质点的接触作用，即微粒和质点并入或分出时发生碰撞而产生微粒速度的突变，从而使质点的速度发生连续的变化；并入或分出以后，作用也就停止。
牛顿第二定律原来只用于常质量物体的运动，但如在两个瞬时考察相同总质量的动量变化，也可用于变质量物体的运动。
设变质量质点的质量m是时间t的函数，即m＝m(t)。在瞬时t，质点的质量为m(t)，质点对于定坐标系Oxyz的速度为v(图1)，即将与之合并的微粒的质量为dm(t)，其对Oxyz的速度为u。在瞬时t+dt，微粒与质点合并。于是质点的质量变为(m+dm)，其对Oxyz的速度成为v+dv。对于质量分出的情况(如火箭)，则dm＜0，即
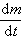为负。
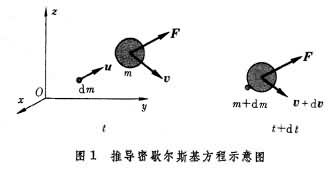
m和dm所组成的质点系在瞬时t的动量为mv+udm;在瞬时t+dt的动量为(m+dm)(v+dv)。在dt时间内，动量的增加dp为：
dp＝(m＋dm)(v＋dv)－(mv＋udm)。将上式展开并略去二阶微量，再根据牛顿第二定律，就得到变质量质点的基本运动微分方程：
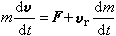， (1)式中vr＝u－v是微粒相对于变质量质点的速度。若把上式右端第二项记为Φ，就得：
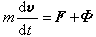。这是变质量质点的基本运动微分方程的另一种形式，是俄国И.В.密歇尔斯基于1897年导出的，称为密歇尔斯基方程。式中F为外力；Φ具有力的量纲，称为反推力。对火箭(图2)来说，Φ就是射流施加在它尾部的推力T，即
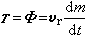，式中vr＝u－v是射流相对于发动机的速度，由于
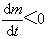，推力 T与相对速度为反向，故火箭在直线运动中的运动微分方程可写作：
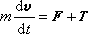，式中F包括诸如重力和空气阻力等外力。这方程表明，火箭由于发动机喷出微粒而受到推力T。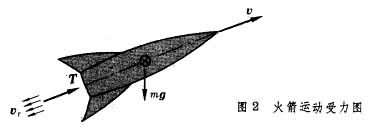
火箭速度公式 设火箭在真空中运动时不受外力(图3)，喷出微粒的相对速度vr的值为常数，其方向与物体的速度v相反而共线。
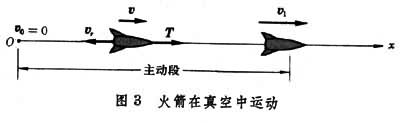
取式(1)两端在x轴上的投影，得：
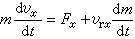，为方便起见，用v代表vx，vr表示相对速度的模，则vrx＝－vr 。又因Fx=0，故上式可写作：
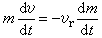或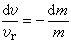
。 (2)设m=m0·f(t)，式中f(t)为确定微粒喷射规律的函数，且当t=0时，f(0)=1，即m0为质点的初始质量。积分式(2)并设t=0时，v=v0，得：
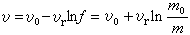。 (3)上式表明，变质量质点的速度同初始质量m0对剩余质量m的比值有关。在v0=0的条件下，设喷射终了时质点的质量为ms（此即燃料烧完时火箭壳体的质量），燃料的质量为mf，则火箭在喷射终了时的速度 v1可从式(3)求得：
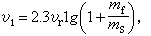(4)此式称为齐奥尔科夫斯基公式。К.Э.齐奥尔科夫斯基是开拓火箭技术领域的先驱者之一。 从式(4)可推出如下结论：① v1与相对速度成正比；②m0/ms或mf/ms越大，则v1越大；③v1与喷射规律f(t)无关，即与燃料的快慢无关(这是不考虑Fx的结果)；④如要提高v1，提高vr比增加m0/ms更为有效。
变质量质点的动量定理 将基本方程 (1)写成如下形式：
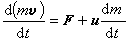， (5)式中
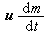是单位时间内喷出微粒的绝对运动所引起的反推力，记为R，则上式可写作：
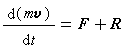， (6)这就是变质量质点的动量定理。将式(6)写作：d(mv)＝Fdt＋Rdt，就得到变质量质点的冲量定理：变质量质点动量的微分，等于外力的元冲量和微粒绝对运动引起的反推力元冲量之和。
变质量质点的动量矩定理 变质量质点对某固定点的动量矩定义为r×mv，式中r为由固定点引出的矢径。在式(6)等号的两边作r的矢量积，得：
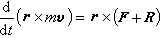，这就是变质量质点的动量矩定理：变质量质点对某一固定点的动量矩的时间导数，等于外力和微粒绝对运动引起的反推力合力对同一固定点之矩。变质量质点的动能定理 变质量质点的动能为：
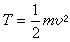。将变质量质点的基本方程(1)的两边各项分别点乘以vdt或dr，移项后得：mv·dv＋v·vdm=F·dr+v·udm， (7)式中左边第一项可写作：
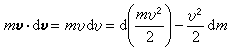。 (8)此外，
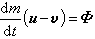是反推力，两边点乘以v，移项后得：v·u dm=Φ·dr+v2dm。 (9)将式(8)、(9)两式代入式(7)，得：
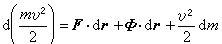；这就是变质量质点的动能定理：变质量质点动能的微分，等于所有外力的元功、反推力的元功和喷出微粒的元质量由于牵连速度而产生的动能之代数和。