劳思方程(卷名：物理学)
Routh equation
一个动力学方程。是E.J.劳思于1876年提出的。他利用广义动量积分（见拉格朗日方程）把拉格朗日方程降阶，得到了仍旧保持拉格朗日方程形式的动力学方程。
一个有N个自由度的保守系统，它有N个广义坐标qi(i=1，2，…，N)。但在这个系统的拉格朗日函数（见拉格朗日方程）L中， 并不包含某些坐标，设为q1，q2，…，qk(k<N)，这些坐标称为循环坐标。对应于循环坐标有广义动量积分
引入劳思函数
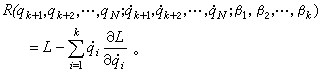就可导出劳思方程
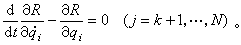上式的形式同保守系统的拉格朗日方程一样，但是式中只有2(N-k)个阶，已降低2k阶，达到了降阶的目的。缺少的循环坐标可用下列积分求出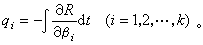
例如，用平面极坐标 (r，Θ)求解平面中质点的辏力的运动问题时，力心选作原点，
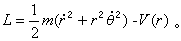式中L不含Θ，所以Θ是循环坐标。循环积分为
(1) 劳思函数为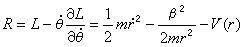
代入劳思方程
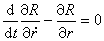，得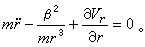
(2)从上式解出r(t)后，应用(1)式可得 
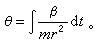这样可求出r和Θ为时间函数，这一力学问题得到解决。