惯量张量(卷名：物理学)
inertial tensor
刚体对于一点的转动惯性的量度。若Oxyz是固连在刚体上的一直角坐标系(图1)，l轴是通过坐标原点O的任意轴，它和各坐标轴Ox、Oy、Oz的夹角分别为α、β、γ;设刚体中任一质点P的质量为mi，它的坐标为(xi，yi，zi)，则刚体对轴l的转动惯量为
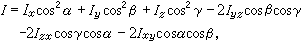式中
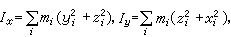
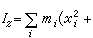
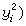为刚体对坐标轴Ox、Oy、Oz的转动惯量。
称为惯性积。惯性积也依赖于刚体的质量、质量分布和各坐标轴的位置。但它的值可正可负，也可等于零。惯性积的量纲和转动惯量相同，即等于ML2。刚体对过坐标原点O 的任意轴l的转动惯量I由六个量Ix、Iy、Iz、Ixy、Iyz、Izx及轴l对坐标轴Ox、Oy、Oz的方向余弦决定。I是由刚体本身的质量、质量分布及轴l的方位来决定的，它是一个具有力学性质的量，它的值不因确定物体位置所选取的坐标系的不同而改变。对称的惯量矩阵：
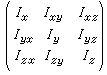是一个张量，称为刚体关于原点O 的惯量张量。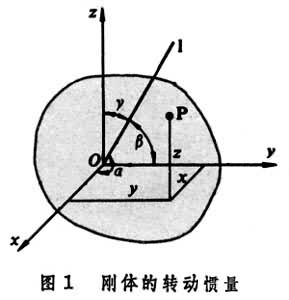
适当选择坐标系Oxyz的方位，可使刚体的两个惯性积同时为零，例如，
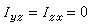，这时，和这两个惯性积同时相关的z轴称为刚体在O点处的一个惯量主轴。一般地说，对于刚体上的任意一点O有三个互相正交的惯量主轴。刚体对惯量主轴的转动惯量称为主转动惯量。如果惯量主轴还通过刚体的质心，则这样的主轴称为中心惯量主轴，刚体对中心惯量主轴的转动惯量称为中心主转动惯量。当刚体绕中心惯量主轴之一转动时，在轴承上将不会由于转动而引起附加的动反力（见刚体的定轴转动）。若Iс尣′、Iсу′、Iсz′为刚体对以中心惯量主轴为坐标轴Cx′、Cy′、Cz′的转动惯量(图2)，则通过O点的任意轴l的转动惯量为
式中α、β、γ为平行于l轴且通过质心C的轴l′和各坐标轴的夹角，m为刚体的质量，s为轴l和轴l′之间的距离。可见，只要知道三个中心主转动惯量，则可求出对任意轴l的转动惯量。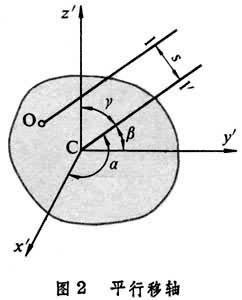
一般说来，确定惯量主轴的方向是困难的。但如果刚体的质量分布具有对称轴，则该对称轴便是惯量主轴，也是中心惯量主轴。若刚体的质量分布具有对称面，垂直于这对称面的任一直线是对于这直线和对称面的交点的一个惯量主轴。如这交点和质心重合，则这轴是一个中心惯量主轴。均匀球体的任意三个互相正交的直径是球体的三个中心惯量主轴。均匀椭球通过质心的三个几何对称轴是椭球的三个中心惯量主轴。