奇异积分的交换子(卷名：数学)
commutator of singular integrals
调和分析中典型的一类非卷积算子。设T1，T2是两个算子（一般说来，设它们的作用次序是不可交换的，即T1T2
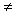T2T1），定义T1与T2的交换子为T1T2－T2T1，记为[T1，T2]，即[T1，T2]＝T1T2-T2T1。如果在L2(R)中取T1＝A为用函数A(x)作乘法的算子，即A(ƒ)(x)＝A(x)ƒ(x)，取T2为奇异积分即希尔伯特变换H或它与微分算子
的整数次幂的乘积，这时所得到的交换子称为奇异积分的交换子。例如，C1(ƒ)=[A，DH]ƒ就是一个奇异积分的交换子。形式地在积分号下取微商，得到
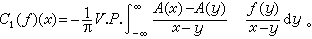注意到H是 L2有界的，容易猜测：只要A′(x)∈L∞，即
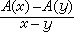本性有界，C1(ƒ)对ƒ来说是L2到L2有界的。但由于这个算子不是卷积算子，这个猜测较难验证。直到1965年才被A.P.考尔德伦用复杂的复分析技巧加以证明。对DnH，与A作n次的交换子运算，便得到高阶奇异积分的交换子（省略一个常数因子）
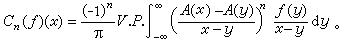考尔德伦的方法不适用于高阶的情形。1975年R.考伊夫曼与Y.迈耶用实分析的方法证明了：若A′(x)∈L∞，则Cn(ƒ)是L2到L2的有界算子。1982年他们与A.麦金托什合作，通过对Cn(ƒ)的算子模作精确的估计，证实了关于李普希茨曲线上柯西积分算子的考尔德伦猜想:若A′∈L∞，则定义在复平面的李普希茨曲线z(x)＝x+iA(x)上的柯西积分算子
是L2到L2有界的。奇异积分交换子的研究，与BMO（有界平均振动）函数有密切联系（见BMO 空间）。例如，1976年R.R.科伊夫曼、R.罗奇伯格与G.韦斯证明了，最简单的奇异积分的交换子
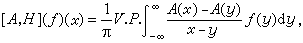对ƒ来说是L2到L2有界的充分必要条件是A为BMO函数，并且交换子的算子模与A的BMO模的大小是差不多的。奇异积分交换子的结果与方法，在调和分析、偏微分方程与非线性分析中有着愈来愈广泛的应用。由于它不是卷积算子，因此，许多古典调和分析的技巧不能直接应用，需要寻求新的方法。
参考书目
A.P.Calderón， Commutators of Singular IntegralOperators，Proc. nat. Acad. Sci. U. S. A.，53， pp.1092～1099，1965.
A.P.Calderón，Commutators，Singular Integral on Lipschitz Curves and Applications，Proc.of the I. C. M.，Helsinki， 1978.
Y.Meyer，Intégrales Singulières， Opérateurs Multilinéaires，Analyse Complexe et Equations aux Derivées Partielles，Proc.of the I.C.M.，Warszawa，1983.