常微分方程运动稳定性理论(卷名：数学)
stability theory of motion in ordinary differential equation
动力系统的运动稳定性的理论，是由俄国数学家Α.М.李亚普诺夫于19世纪90年代所开创。它是研究扰动性因素对运动系统的影响。这种扰动性因素，可以是瞬间的作用，引起系统的初始状态的变化；也可以是持续地起作用，而引起系统本身的变化。通常着重考虑的是前者。微小的扰动对于不同的系统运动的影响是不一样的。对有些运动，影响不显著，受扰动的运动与未受扰动的运动相差很小。而对有些运动，扰动的影响可能很显著，以致无论扰动如何小，受扰动的运动与未受扰动的运动随时间的推移可能相差很大。简略地说，属于前者的运动是稳定的，属于后一类型的运动是不稳定的。运动稳定性理论就是要建立一些准则，用来判断所考虑的运动是稳定的或不稳定的。
一般，动力系统的数学模型可写成
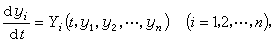(1)式中yi是某些与运动有关的参数，例如坐标和速度，或者一般地是这些量的某些函数。方程(1) 的解称为运动。要研究的是当初值条件有微小变化时，是否会引起解的微小变化。考虑这个系统的任何特殊运动，它相应于(1)的某个特解
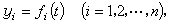称这个特解是未受扰动的运动，以区别于这个系统的其他的运动；而称后者为受扰动的运动。量yi是受扰动的运动与未受扰动的运动的差值称为扰动。如果对于任意正数 ε，无论它多么小，总可以找到另一个正数 η（ε），使得对于所有受扰动的运动 yi＝yi(t)(i=1，2，…，n)，只要在初始时刻t=t0满足不等式
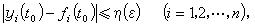(2)就在所有t≥t0时满足不等式
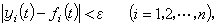(3)则称(1)的未受扰动的运动对量yi 是稳定的；否则，称它是不稳定的。由此可知，如果存在某个固定的数ε，对于无论多么小的数 η，即使只有一个受扰动的运动，它满足不等式(2)，但在某一时刻，不等式(3)中只要有一个变为等式，那末未受扰动的运动就是不稳定的。如果未受扰动的运动不但是稳定的，而且当初始扰动足够小时，随着 t的无限增加，所有受扰动的运动都逐渐趋近于未受扰动的运动，就称未受扰动的运动是渐近稳定的。为了研究方程(1)的特解yi=ƒi(t)(i=1，2，…，n)的稳定性问题，一般比较困难。为此，对方程(1)引进坐标变换
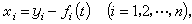(4)于是有
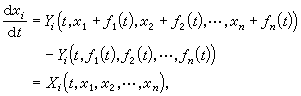(5)显见
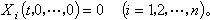
这样，就可以把研究方程组(1)的特解yi=ƒi(t)(i=1，2，…，n)的稳定性问题化为研究系统(5)的平凡解xi=0(i=1，2，…，n)的稳定性问题。
此时，不等式(2)及(3)分别变成
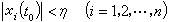(6)及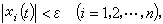
(7)因而上述稳定性定义可以表述如下：如果对于任意正数ε，无论它多么小， 都可以选取另一个正数 η(ε)， 使得对于所有受干扰的运动xi=xi(t)(i=1，2，…，n)，只要在初始时刻t0时满足不等式(6)，就在所有t≥t0时满足不等式(7)，则称(5)的未受扰动的运动xi=0(i=1，2，…，n)是稳定的。否则，则称 xi=0(i=1，2，…，n)是不稳定的。
如果未受扰动的运动xi=0(i=1，2，…，n)是稳定的，并且数 η可选得如此之小，使得对于所有满足不等式(6)的受干扰运动，都满足条件
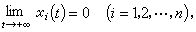则称xi=0 (i=1，2，…，n)是渐近稳定的。这就是李亚普诺夫在他的博士论文《运动稳定性一般问题》(1892)中所给出的有关常微分方程解的稳定性定义，通常称为李亚普诺夫意义下的稳定性。它有下列几个特点：①首先，李亚普诺夫稳定性概念是一个局部概念，它涉及到在被考虑的状态附近的特性，因此初始扰动的范围较小，即η值较小；②时间t取值在无限长区间[t0，+
)上；③初始扰动的大小与初始时刻t0的选取无关；④在初始扰动后无其他外界干扰；⑤未受扰动的运动与受扰动的运动服从于同一个方程，而且对二者在同一时刻进行比较。由于在一般情况下所研究的微分方程，它的解都不能求出来，因此李亚普诺夫在他的上述论文中，提出了两种解决问题的方法，称之为李亚普诺夫第一方法和第二方法。
李亚普诺夫第一方法 基于研究微分方程组的通解或特解而研究受扰动运动的所有方法，都归属为第一方法。这个方法一般需要去寻求按任意常数的正整数幂的无穷级数或具有另一些特征的级数形式的解，故又称幂级数展开法。考虑微分方程组
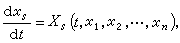(8)
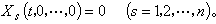设(8)的右端函数可展成 x1，x2，…， xn 的幂级数，即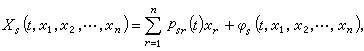
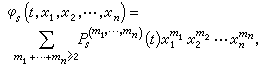(9)式中系数psr(t)，
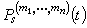对一切t∈[t0，+
)连续、有界，且满足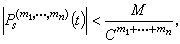
(10)式中M，C是与t，s，m1，…，mn无关的正常数。李亚普诺夫将(8)的解写成下述形式的级数
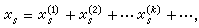(11)将(11)形式地代入（8），并将其右端φs(t，x1，x2，…，xn)重新写成形如
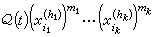为项的新的幂级数，其中Q(t)表示t的函数。用R扤表示这个新的幂级数中m1h1+…+mkhk=m的一切项的有限和。再令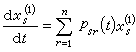
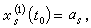(12)
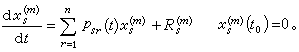(13)显然R扤仅依赖于 
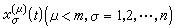和(9)的系数psr(t)及 
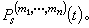因此，由(12)、(13)可逐项地确定x扏，x扐，…，从而形式地得到级数（11）。李亚普诺夫证明：给定任意有限区间[t0，T](T>t0)，存在常数A，0<A<C，使得对于一切初值α=(α1，α2，…，αn)，‖α‖≤A，级数(11)对一切t∈[t0，T]和‖α‖≤A绝对且一致收敛，且xs(t)是(8)的满足xs(t0)=αs(s=1，2，…，n)的惟一解。进一步，在另一些附加条件下，他还证明了：对一切t≥t0，所得的(11)仍是(8)的解，即证得在区间[t0，+
)上解的存在性，从而得出关于解的稳定性的结论(见下面定理)。这表明李亚普诺夫存在定理，原则上不同于柯西-皮卡存在定理，它不仅在稳定性方面，而且在常微分方程理论中有非常重要的作用。李亚普诺夫在他研究的第一方法中，引入下述重要概念。
① 特征数 设ƒ(t)是定义在t∈[t0，+
)上的连续函数，若存在实数λ，对任何实数ε>0，有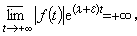
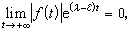称λ为函数ƒ(t)的李亚普诺夫特征数，简称特征数。记成ⅹ{ƒ}＝λ。如果对一切实数λ都有 
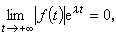定义ⅹ{ƒ}＝+
；如果对一切实数λ都有
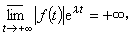定义 ⅹ{ƒ}=-
，函数ƒ（t）的特征数 ⅹ{ƒ} 可用公式
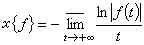计算。函数组x(t)=(x1(t)，x2(t)，…，xn(t))的特征数记成ⅹ{x1(t)，ⅹ2(t)，…，xn(t)}或ⅹ{x(t)}，它定义为ⅹ{x(t)}＝min{ⅹ{x1(t)}，ⅹ{x2(t)}，…，ⅹ{xn(t)}}。李亚普诺夫建立了具有连续、有界系数的线性微分方程组
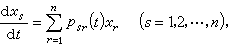(14)的解的特征数的一般理论：(14)的一切非平凡解都有有限的特征数;它不可能有多于n个特征数互异的非平凡解；它的任意一个基本解系的特征数之和s满足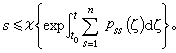
② 正规解系 (14) 的一个基本解系称为正规解系，如果由这个解系中的任一些解作非零系数的线性组合得出来的解的特征数等于参加这个组合的解的特征数的最小者。李亚普诺夫证明：具有连续、有界系数的线性微分方程组(14)必有正规解系；它的一个基本解系为正规解系的充分必要条件是它的特征数之和s达到最大值。
③ 正则系统 (14)称为正则系统，如果(14)的正规解系使得 s+μ＝0，其中
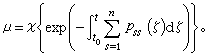(14)称为非正则系统，如果它的正规解系使得s+μ<0。李亚普诺夫第一方法关于稳定性的定理是：设方程组 （8）满足条件 （9）、（10），其中系数psr(t)、
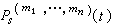是t在[t0，+
]上的连续、有界函数；又设（8）的一次近似系统（14）是正则系统，它的所有特征数都是正的。则(8)的零解 x1=x2=…=xn=0是渐近稳定的。定理中加之于φs(t，x1，x2，…，xn)的条件可以减弱。例如，只需假设φs在域│xs│≤H(s=1，2，…，n)，t≥t0中满足条件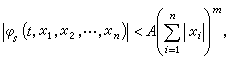
其中A>0，m>1为常数，并保证(8)的初值问题的解的存在、惟一性。常系数线性系统和周期系数线性系统都是正则系统。常系数线性系统的特征数是该系统的特征根的实部反号。周期系数线性系统的特征数是该系统的特征指数的实部反号。由此可相应地得出当(8)的一次近似系统 (14)为常系数系统或周期系数系统时，关于(8)的零解为渐近稳定的定理（见线性常微分方程）。
李亚普诺夫同时还证明，如果 (8)的一次近似系统(14)不是正则系统，即s＋μ＝-σ<0，而(14) 的所有特征数λk>σ ，其他条件仍如定理所述， 则(8)的零解是渐近稳定的。
李亚普诺夫第一方法依赖于一次近似系统的特征数的研究。特征数在变系数线性方程组中的地位，犹如特征根在常系数线性方程组中的地位那样重要。这些数表征出当t→+
时解的增长程度，故它在研究解的渐近性态时，有其根本意义。但是决定变系数线性方程组解的特征数是很困难的。线性方程组的微小变化是否也只引起特征数的微小变化？И.Γ.马尔金于1952年提出线性方程组的特征数稳定的概念，并建立了判定线性方程组的特征数稳定的若干准则。Б.Ф.贝洛夫等人，不仅对扰动是线性项的系统，而且对扰动是非线性项的系统的最大（小）特征数的上（下）稳定问题和特征数的重合问题，作了深入的研究。至今，特征数理论已经向多方面发展。以一次近似判定非线性系统的稳定性问题，除上述李亚普诺夫工作外，Ο.佩隆、К.∏.佩尔西德斯基、马尔金和R.贝尔曼等人都做过大量的研究。值得指出的是，佩隆举例说明，对于满足上述条件的任意φs，仅由一次近似方程组(14)的零解渐近稳定性，还不足以保证非线性方程组(8)的零解的稳定性。
李亚普诺夫直接法 即李亚普诺夫第二方法，它不需要寻求运动方程的特殊解。把未受扰动的运动的稳定性归结为平衡位置（即(5)的平凡解xi=0(i=1，2，…，n)的稳定性问题后，李亚普诺夫将稳定或者不稳定的事实与某些具有特殊性质的函数 V(x1，x2，…，xn)的存在性联系起来。这个函数沿着轨线对时间 t的全导数具有某些确定的性质。例如，方程
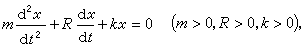(15)等价于
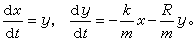(16)作系统的总能量函数
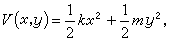(17)它沿(16)的轨线关于t的全导数
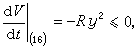故知(16)的平凡解是稳定的。又如对方程组
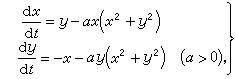(18)作函数
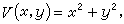(19)则
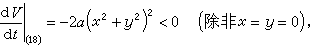(20)且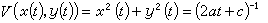
(c是任意正常数)。因此
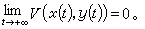即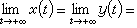
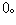故知(18)的平凡解是渐近稳定的。(20)说明了封闭曲线族x2+y2=C沿着(18)的相轨线按t的增加方向不断地收缩，直至收缩到原点。换句话说，(18)的相轨线随着t的增加由外向里地穿过每一条闭曲线V(x，y)=C，最终趋于原点。这里，函数(19)表示了在相平面上由(18)所描述的运动质点与原点之间的距离平方。因此
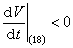(当x2+y2≠0)就表示了这个距离随着时间的增长在不断地减小，并最终趋于零。前面的函数(17)亦具有与(19)同样的性质。从上述两例可以看出：研究由常微分方程组来描述的动力系统的稳定性时，可以不必去求它的特解与通解，而是构造一类具有特殊性质的函数V(x，y)，由这个函数来控制相轨线的动向，来解决未被扰动运动的稳定性问题。称这种类型的函数V 为李亚普诺夫函数。它有各种构造方法，一般要结合实际的物理背景来作。
通常总假定函数V在坐标原点邻域内连续单值，V(0，0，…，0)=0，且有连续的偏导数。称函数V(x1，x2，…，xn)为定号的（正定的或负定的），如果当│xs│≤h（h是足够小的正数，s=1，2，…，n）时，它只能取具有固定符号的值，且只在xs=0(s=1，2，…，n)时，取零值。称V(x1，x2， …， xn) 为常号的（正的或负的），如果它在区域|xs|≤h(s=1，2，…，n)内只能取具有一定符号的值，但它可以在
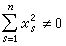时取零值。称 V(x1，x2，…，xn)为变号的，如果它既不是定号的，也不是常号的，亦即，无论数h多么小，它在区域内既可取到正值，也可取到负值。通常取二次型作为李亚普诺夫函数，这是用得最广泛的一种。下面介绍李亚普诺夫关于稳定性的几个定理。
考虑自治系统（或称驻定系统，即方程右边与t无关的系统）
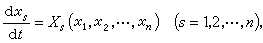(21)假定函数Χs(x1，x2，…，xn)在区域│xs|≤h(s=1，2，…，n)内连续，且使得方程(21)过区域内的任一点(x10，x20，…，xn0)有且只有一个解，Χs(0，0，…，0)=0(s=1，2，…，n)，则有：定理 1 如果可以找到一个定号函数 V (x1，x2，…，xn)，它关于时间t的由(21)构成的全导数
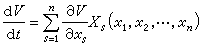是常号函数，且其正负号与V相反或者恒等于零，则(21)的未被扰动运动xs=0(s=1，2，…，n)是稳定的。定理2 如果可以找到定号函数 V(x1，x2，…，xn)，它对于时间t由(21)构成的全导数也是定号的，但是其正负号与V的正负号相反，则(21)的未被扰动运动xs=0(s=1，2，…，n)是渐近稳定的。
定理3 如果可以找到函数V(x1，x2，…，xn)，它对于时间t由(21)构成的全导数是定号函数，而函数V本身却不是与
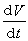的符号相反的常号函数，则(21)的未被扰动运动xs=0 (s=1，2，…，n)是不稳定的。定理4 如果存在函数V(x1，x2，…，xn)，它对于时间t由(21)构成的全导数为
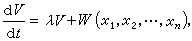其中λ>0是常数，而 W(x1，x2，…，xn)或者恒等于零，或者是常号函数，并且在后一种情形，V不是与 W 的符号相反的常号函数，则(21)的未被扰动运动xs=0(s=1，2，…，n)是不稳定的。在定理3中，要求导数
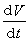是定号的这个条件可以削弱，如果代之以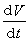在V>0的区域内的所有点上都取正值，则定理的结论仍然是正确的。首先指出这一点的是H.Γ.切塔耶夫。他得到如下定理：如果对于(21)可以找到如此的函数V(x1，x2，…，xn)，使得:①在坐标原点任意小的邻域存在V>0的区域，在它的边界上V=0;②在区域V>0的所有点上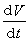，取正值。则（21）的未被扰动运动是xs=0 (s=1，2，…，n)不稳定的。E.A.巴尔巴申和H.H.克拉索夫斯基给出了关于渐近稳定性定理的改进，其特点是借助于有常号导数的李亚普诺夫函数来解决渐近稳定性问题，且将其推广到全空间，得到如下的定理：如果对于方程组(21)存在正定函数V(x1，x2，…，xn)，使得
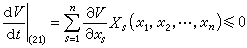且使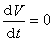
的集合中除原点外不包含整条正半轨线，那么(21)的未被扰动运动xs=0(s=1，2，…，n)是渐近稳定的。对于非驻定系统，李亚普诺夫类似地建立了判断未被扰动运动稳定、渐近稳定和不稳定的定理。
运用上面的定理，李亚普诺夫还研究了一次近似为常系数的非线性系统的零解的稳定性问题。特别是对于特征方程中有一个零根或两个零根或一对共轭纯虚根、而其他根都具有负实部这三种临界情形都作了仔细分析；对于一次近似是周期系数的情形，他分析了特征方程中有一个根等于1和有两个共轭虚根具有模等于1的情形。
前面已指出：李亚普诺夫意义下的稳定性质是局部性的概念，但处理局部问题的李亚普诺夫函数的思想方法，完全可推广到全相空间。事实上，在50年代初，人们对自动调节系统的研究中所遇到的卢里耶问题以及奥泽尔曼问题就出现过初始扰动任意大的情形，从而很自然地要去研究未被扰动运动的全局渐近稳定性问题。此时(21)的右端函数是在全空间Rη上满足保证解的存在惟一性条件。不妨设xs=0(s=1，2，…，n)是(21)的惟一奇点。如果(21)的零解是稳定的，并且对于(21)的所有解，都有
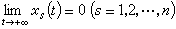则称(21)的零解是全局渐近稳定的。巴尔巴申和克拉索夫斯基引进无限大函数的概念，即:如果函数V(x1，x2，…，xn)对任何大的数K>0，都存在数R>0，使得只要
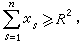就有|V(x1，x2，…，xn)|>K，则称函数 V具有无限大性。他们很自然地把李亚普诺夫的局部渐近稳定性定理推广到全空间，得到下述定理:①如果存在定号无限大函数V(x1，x2，…，xn)，它关于t的由方程组(21)构成的全导数
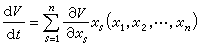是与V 符号相反的定号函数，则(21)的零解是全局渐近稳定的。②如果存在定号无限大函数 V(x1，x2，…，xn)，它关于t 的由方程组(21)构成的全导数是与V 符号相反的常号函数，且集合
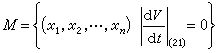中除了零解外不含有方程组(21)的任何正半轨线，则方程组(21)的零解是全局渐近稳定的。这两个定理为全局渐近稳定性理论奠定了基础。J.P.拉萨尔更联系解的ω极限集（见拓扑动力系统）建立了不变性原理：设 G为Rn中列紧集，从 G出发的方程组(21)的轨线， 在未来时刻仍保留在集G 中；如果在G 内存在函数 V（x1，x2，…，xn），使
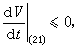记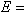
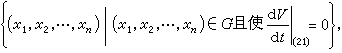又M是E中的最大不变集，则由G内出发的(21)的每一条轨线当t→+
时必趋向于M。显然，如果G＝Rn，M＝{(0，0，…，0}，且(21)的一切解均有界，则(21)的零解是全局渐近稳定的。自动调节系统的稳定性在现代工业中的作用是众所周知的。调节系统分直接调节系统和间接调节系统两大类。它们的数学模型分别是
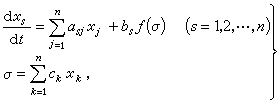(22)或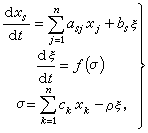
(23)式中αsj、bs、сs(s，j=1，2，…，n)是常数，又ƒ(σ)满足
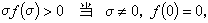(24)如果对任何满足(24)的ƒ(σ)，方程组(22)的零解x1=x2=…=xn=0（或(23)的零解 x1=x2=…=xn=ζ=0）是全局渐近稳定的，则称方程组（22）（或方程组(23)）在角(0，
)内是绝对稳定的。判定绝对稳定的主要途径是选取正定无限大函数，给出条件保证其全导数是负定的。除了上述一些类型的稳定性外，还有如李亚普诺夫研究过的有关部分变元的稳定性。马尔金研究过的经常扰动下的稳定性。拉萨尔、S.莱夫谢茨指出的实际稳定性，以及目前蓬勃发展的大系统稳定性，还有与动力系统有密切联系的轨道稳定与结构稳定性等等。
随着科学技术的迅速发展，李亚普诺夫创立的运动稳定性理论，不仅在力学、控制、工程及星际航行等科学尖端技术领域有其广泛深刻的应用，而且在现代物理、生物、化学等自然科学中得到了进一步的发展，同时它亦逐渐发展成为常微分方程学科本身许多课题理论研究的有力工具。李亚普诺夫稳定性理论中的一个核心问题，就是李亚普诺夫函数的构造问题。30多年来人们作了不少的努力，但对于一般非线性系统，还没有得到通用而有效的构造方法。虽然如此，针对实际问题中出现的各种非线性系统，通过定性分析并根据实际情况进行具体分析，从而构造出恰当的李亚普诺夫函数，还是取得了丰富的成果。