拉格朗日方程(卷名：力学)
Lagrangeˊs equations
对于完整系统用广义坐标表示的动力方程，通常系指第二类拉格朗日方程，是法国数学家J.-L.拉格朗日首先导出的。它可写成：
， (1)式中T为系统用各广义坐标qj和各广义速度妜j所表示的动能；Qj为对应于qj的广义力;N(=3n-k)为这完整系统的自由度；n为系统的质点数；k为完整约束方程个数。完整的约束方程为：
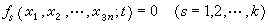。 (2)因此，3n个x不是互相独立的，独立的只有N个，因而可用N个广义坐标q1，q2，…，qN来描述这个系统，即3n个x可表成N个q的函数：
。 (3)应用以上坐标变换于下列动力学普遍方程：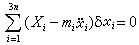
，则得到用N个广义坐标qj(j=1，2，…，N)表示的方程：
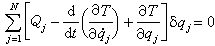。由于N个δqj(j=1，2，…，N)是互相独立的，上式N个括号中的各项之和都必须为零，所以就得到式(1)。将式(3)对时间全微分，得：
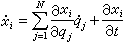。将上式代入系统的动能表达式，得：
式中T2为T中广义速度妜的二次齐次式；T1为妜的一次齐次式；T0中不含妜；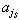
、bj、T0只是广义坐标q和时间t的函数。当约束方程(2)不含t时，T=T2。在分析力学中推导式(1)时，用到以广义速度表示的T式。但是在实际问题中，往往可直接从被研究对象的运动特性求得T，无须用这样繁复的坐标变换法。广义力Qj可从虚功元的关系式δWj=Qjδqj中直接求得。用上述方法求得T和Qj，就很容易列出实际问题的完整系统动力方程。
对于保守系统存在着势函数V(q1，q2，…，qN)，则广义力为
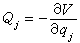。又因V中不含妜j， 所以
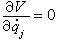。令L=T-V，则式(1)可改写作：
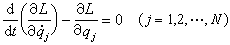， (4)式中L称为拉格朗日函数，又称动势。式(4)称为完整保守系统的拉格朗日方程。它不但形式简单，而且与变分问题中的欧拉方程形式相同，由此可导出哈密顿原理。用拉格朗日方程解题的优点是：①广义坐标个数通常比x坐标少，即N＜3n，故拉氏方程个数比直角坐标的牛顿方程个数少，即运动微分方程组的阶数较低，问题易于求解;②广义坐标可根据约束条件作适当的选择，使力学问题的运算简化，并且不必考虑约束力；③T和L都是标量，比力的矢量关系式更易表达，因此较易列出动力方程。下面是两个例子：
①图1是一个半径为a、质量为m1的圆盘，它的中心用铰链与质量为m2的直杆相连。 此杆的另一端用铰链固接在半径为b的空心圆筒的中心O;杆长l=b-a。圆盘绕O点摆动。杆的动能为
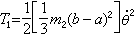；圆盘转动角关系为bθ＝a(θ+嗞)； 圆盘绕O点转动动能为
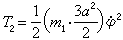；系统以B点为标准的势能V和系统的动能T为：
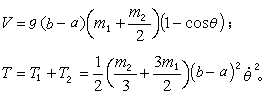代入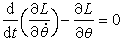
，可得系统的运动方程： 
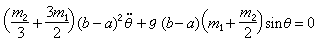或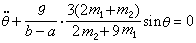
。②图2是以刚度为k1、k12、k2的三根弹簧水平连接质量为m1、m2的两个质点。若以两质点的平衡位置为起点的水平位移x1、x2作为广义坐标，则两质点的动能T和势能V为：
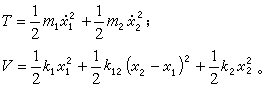代入下列两个方程：
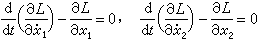，可得两质点的运动方程：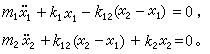
第一类拉格朗日方程是用直角坐标表示的动力学普遍方程与用k个未定乘子和直角坐标表示的k个约束方程(包括微分约束)相结合而成的方程。这组方程可以解决用直角坐标描述的动力学问题和非完整系统的动力学问题。此方程还可变换成广义坐标表示的费勒斯方程，以求解一般包含线性速度约束的非完整系统的动力学问题。
参考书目
E.T. Whittaker， A Treatise on the Analytical Dynamicsof Particles and Rigid Bodies，4th ed.，Cambridge Univ.Press，Cambridge，1952.
H. Goldstein， Classical Mechanics， 2nd ed.，Addison Wesley，Reading，Massachusetts，1980.
W.Hauser， Introduction to the Principles ofMechanics， AddisonWesley，Reading， Massachusetts，1965.