广义坐标(卷名:物理学)
generalized coordinates
能确定地描述一个体系运动的独立变数,常用q来表示。对N个自由度的完整体系(见约束)而言,它的广义坐标有N个(q1,q2,…,qN)。
例如有一点固定的刚体,它的自由度为三,广义坐标可用三个欧拉角 (θ,嗞,ψ)表示(见刚体的定点运动)。
对于非完整体系(见约束),尚有不可积的微分约束,速度受约束方程的限制,由于不可积,相应的坐标仍未受限制,这样广义坐标仍由有限约束决定。设n个质点的质点系受有h个有限约束,k个微分约束,则广义坐标个数仍为3n-h,大于它的自由度N=3n-h-k。
N个广义坐标的任何N个单值可微函数
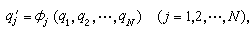
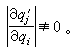
例如对空间中的一个质点而言,其直角坐标(x, y,z);球面极坐标(r,嗞,θ);圆柱坐标(z,ρ,θ)都可看作广义坐标。
广义坐标的广泛选择性,正是应用这种坐标的优点。这种坐标首先出现于J.L.拉格朗日著的分析力学中。广义坐标这个术语是开尔文在1876年提出的。