广义相对论(卷名:数学)
general theory of relativity
A.爱因斯坦所提出的引力理论。这一理论把引力场和时空结构联系起来,引入了四维洛伦茨流形作为现实时空的模型,这种流形的几何学在很小范围中接近于四维闵科夫斯基空间R3,1的几何学,但从较大范围来看,它和闵科夫斯基空间有显著的差别,是一种弯曲的时空。
一个四维的洛伦茨流形M4,是具有洛伦茨度量的四维微分流形。其意义如下:在M4的每点x的切空间Tx,均定义了向量的内积,但和黎曼流形的情况不同,这种内积不是欧几里得式的,而是闵科夫斯基式的(见闵科夫斯基空间)。对M4的每一坐标邻域,可在其中各点x的切空间Tx中引入自然标架,即由4个切向量
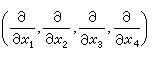 所组成的标架。参考于这个标架,Tx的任一切向量λ可表示为
所组成的标架。参考于这个标架,Tx的任一切向量λ可表示为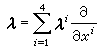 ,两个向量λ ,μ的内积应具形式
,两个向量λ ,μ的内积应具形式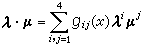 ,这里(gij)构成一个符号为(+,+,+,-)的对称阵。M4在这个坐标区域中的洛伦茨度量就用
,这里(gij)构成一个符号为(+,+,+,-)的对称阵。M4在这个坐标区域中的洛伦茨度量就用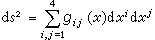 来表示。
来表示。和黎曼几何一样,依据流形的度量,可以作它的克里斯托费尔记号(列维-齐维塔联络),曲率张量和里奇张量。由于曲率张量一般不是0,所以说广义相对论的时空是弯曲的时空。依照切空间的内积,流形的切向量可分为类时、类空、类光等三类,粒子运动的轨线就表示为M4的一条曲线,称为世界线,它的切向量不能是类空的。
爱因斯坦的广义相对论的基本思想是:四维时空的几何结构和其中的物质分布与运动是互相联系的,这种联系可以用引力场方程
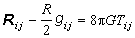 来表示,这里
来表示,这里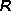 ij是里奇张量,R是数量曲率,G是引力常数,
ij是里奇张量,R是数量曲率,G是引力常数,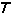 ij是表示物质分布和运动的能量动量张量。特别在真空区域中就应成立。
ij是表示物质分布和运动的能量动量张量。特别在真空区域中就应成立。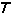 ij=0
ij=0广义相对论的另一基本思想是:在具物质分布的时空中,一个质量很小的只受引力场作用的试验质点的运动轨线(世界线)就是这个洛伦茨流形的测地线,从而使引力场理论成为一种几何的理论。到20世纪30年代,A.爱因斯坦和L.英菲耳德还指出,这一结论事实上可以作为场方程的推论。
在广义相对论中,一般说来并不明显地分出一个时间坐标和三个空间坐标,但是,在这时空中一个运动着的观察者仍然可以把他自己所经历的时空历程记录下来,如有两个曾瞬时会合在一处的观察者,通过不同的运动轨线而重新会合时,就会发现,他们所记录的最终“时空位置”是互不相同的,这便是时空弯曲性的体现。
利用切空间的洛伦茨标架,可以把狭义相对论中的各种物理量在广义相对论中表述出来,这种物理量的变化规律一般可以用微分方程描述,由于现在可以选取的坐标比狭义相对论时广泛得多,所以爱因斯坦要求物理规律在不同的坐标系中的表示形式应该是依一定的规则(符合群的要求)都可以互相转换的,这便是广义相对性原理。
但是,在广义相对论中,如同一切几何问题一样,特殊坐标的选取仍然有其重大的意义。例如,在考虑一个球状物体对周围的真空所产生的引力场时,就可以选取特定的坐标,而得出施瓦茨希尔德解,通过这个解,可以对下列现象进行精确的计算。
① 水星近日点的进动;
② 光线通过太阳附近受引力场影响而产生的弯曲;
③ 光谱因引力而产生的向波长长的方向的偏移(称为引力红移)。
这三个现象的实验验证,使广义相对论的地位得以巩固下来。
广义相对论有许多数学问题需要研究,例如:
① 柯西问题和奇点 已知某一时刻的时空结构、物质分布和瞬时运动,求未来(或追溯过去)的时空结构和物质分布与运动。对小范围和短时间,问题已得到解决,但对长时间来说,可能要产生奇性。如何解释奇点还有许多不清楚的地方,除了时空强烈弯曲外,这还和物质的高度密集状态下的物理性质有关。
② 引力场方程的精确解 尽可能多地作出引力场方程的有物理意义的精确解,除施瓦茨希尔德解外,最著名的还有克尔解等等。
③ 引力波 依照广义相对论,引力作用并不是超距的,而是在时空中传播的,人们很希望能接受到它,由于引力波很微弱,要接收到引力波是一件很困难的事。
④ 时空的大尺度结构 人们希望对我们所处的时空能有一个整体的描述,这已成为一门专门的学问,即“宇宙论”,它必须用到整体的微分几何。
⑤ 引力场的微观结构 即引力场的量子化问题,问是否存在某些“引力子”作为引力场的媒介。
⑥ 引力作用和其他三种相互作用 (电磁、弱、强)的统一理论。
爱因斯坦在研究广义相对论时,得到了数学家M.格罗斯曼的帮助,在他掌握了黎曼几何和张量分析之后,才完成了他的理论,而广义相对论的近年的发展则受到整体微分几何的强烈影响。许多研究都用到整体微分几何,例如,施瓦茨希尔德解,克尔解的整体结构的分析,使人们认为大质量星体在发展的晚期在引力作用下可能会坍缩为“黑洞”,它具有极强的引力,使得在经典理论意义下,物质(包括光)均只能进入黑洞而不能逃逸,又如在渐近平坦的时空结构中,已可严格论证,引力现象必须由正的质量所产生(正质量猜测)。
另一方面,黎曼几何的研究是由于受到了广义相对论的影响而蓬勃发展起来的,近年来,洛伦茨流形的整体微分几何学也处于很活跃的状态。