伪随机数(卷名：数学)
pseudo-random numbers
在数字计算机上用数学方法产生的、统计意义下具有在区间（0，1）上均匀总体简单子样性质的数值序列{rn｜n=1，2，…；0≤rn≤1}。
用蒙特卡罗法模拟求解一个实际问题，要用到各种不同分布的随机变量、随机向量和随机过程 η的抽样序列{ηn｜n=1，2，…}，称它们为随机数。如常用的二项分布随机数、均匀分布随机数、二维正态分布随机数等，其中最基本、最重要的是区间(0，1)上均匀分布的随机数。因此，如何在计算机上产生伪随机数备受重视。
在一台b)进制（如二进制或十进制）、尾数字长为k位的计算机上，不考虑符号和阶码，可以表示bk个不同的数，即0，1，2，…，bk-1。在数学计算机上产生伪随机数，就是选取m个整数x1，x2，…，xm作为初值和一个适于递推计算的数学公式
，把0，1，2，…，bk-1或其中的部分序列的自然顺序打乱重排，得到一个确定的、周期的、又在统计意义下具有在区间(0，1)上均匀总体简单子样性质的数值序列
，以此作为区间(0，1)上均匀分布的随机数使用。序列{rn}是完全确定的，具有周期性，不同于真正均匀分布的随机数，故称为伪随机数。在计算机上用数学方法产生随机数，具有易于实现、产生的速度快和对模拟求解的问题可以进行复算检查等许多特点，成为计算机上最常用的一类产生均匀分布随机数的方法。选用不同的递推计算公式
，就得到了不同的产生伪随机数的方法。为得到产生速度快的算法，多取m＝1，给出一个最大长度不超过bk的不重复的数序列。这类方法中，有早期提出的中平法、乘积取中法和移位相加法等；比较常用的有线性、非线性移位寄存器法及同余法等。在同余法中，又可分为加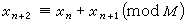同余法
，乘同余法
和混合同余法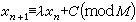
，λ为某一乘子，其中最常用的为乘同余法。这里，模M通常取为bk或bk-1（当bk-1为素数时）；x呏y(modM)为同余式，表示x、y按模M同余。在一台尾数字长为k位的二进制计算机上，取模M=2k，乘同余法的递推计算同余式为
。可以证明，乘同余法的最大可能周斯为2
(k>2)。取乘子λ=8α±3，初值x1=2b+1（α，b为任意正整数）且λ的二进制表示中0、1的出现不规则时，就可以得到周期长为2且统计性质较好的伪随机数
。对产生的伪随机数，要经过一定的理论分析和各种统计检验，以检查得到的序列是否具有在区间(0，1)上均匀总体简单子样所应具有的各种统计性质，如分布的均匀性、取值的随机性、前后的独立性和分段序列统计性质的一致性等。进行上述统计性质检验的方法很多，常用的有参数检验、均匀性检验、独立性检验、连检验和各种不同的组合规律性检验等。
有了伪随机数{rn}，利用各种不同的抽样算法，如直接抽样、变换抽样、舍选抽样、复合抽样等，就可以产生模拟计算中需要的各种不同分布的随机数。
设随机变量η的分布函数F(x)连续，逆函数F -1(y)存在，则R=F（η）为区间（0，1）上均匀分布的随机变量。利用这一原理，从随机数{rn}出发，就可以直接得到η的抽样序列
如果随机变量η具有密度函数 
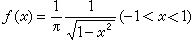，利用直接抽样，得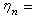
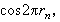常称为随机余弦。在概率统计的理论研究和实际应用中，经常遇到具有密度函数
的正态随机变量。由随机数{rn}出发，利用二元函数变换进行抽样，由
给出一对均值为0、方差为1的相互独立的正态随机数。上述抽样算法，要用到对数、开方、正弦和余弦等算法，速度较慢。在计算机上，灵活多变、计算量省的舍选抽样和复合抽样更经常的用来产生所要的各种不同分布的随机数。以随机余弦
为例，舍选抽样算法的过程为：产生一对伪随机数r1、r2;当
时，舍去r1、r2，再产生一对新的伪随机数；否则，
记φ为(0，2π)上均匀分布的随机数，得随机余弦和随机正弦的抽样值
参考书目
中国科学院计算中心概率统计组编著: 《概率统计计算》，科学出版社，北京，1979。
徐钟济编著：《蒙特卡罗方法》，上海科学技术出版社，上海，1985。