塑性力学(卷名：力学)
plasticity
固体力学的一个分支，研究物体超过弹性极限后所产生的永久变形和作用力之间的关系以及物体内部应力和应变的分布规律。和弹性力学的区别在于，塑性力学考虑物体内产生的永久变形，而弹性力学不考虑；和流变学的区别在于，塑性力学考虑的永久变形只与应力和应变的历史有关而不随时间变化，而流变学考虑的永久变形与时间有关。
塑性力学理论在工程实际中有广泛的应用。例如用于研究如何发挥材料强度的潜力，如何利用材料的塑性性质，以便合理选材，制定加工成型工艺。塑性力学理论还用于计算残余应力。
基本实验和基本理论 对塑性变形基本规律的认识来自实验。从实验中找出在应力超出弹性极限后材料的特性，将这些特性进行归纳并提出合理的假设和简化模型，确定应力超过弹性极限后材料的本构关系，从而建立塑性力学的基本方程。解出这些方程，便可得到不同塑性状态下物体内的应力和应变。
基本实验 基本实验有两个：
①简单拉伸实验 对某些材料（如低碳钢）作简单拉伸实验，可得到如图1所示的应力-应变曲线。实验表明，应力-应变曲线上存在一个称为弹性极限的应力值，若应力小于弹性极限，则加载和卸载的应力-应变曲线相同（OA段）;若应力超过弹性极限，加载的应力-应变曲线有明显的转折，并出现一个水平的线段（AF），常称为屈服阶段，相应的应力称为屈服极限。弹性极限、屈服极限的值相差不大，在工程上常取为一个值，仍称屈服极限，记为σ
。材料中的应力达到屈服极限时，材料即进入塑性阶段。此阶段的最大特点是：加载和卸载的应力-应变曲线不同。例如由图1中B点卸载，应力与应变不是沿BAO线而是沿BD线退回。应力全部消失后，仍保留永久应变OD。实验表明，在变形不大时，多数材料应力-应变曲线中的BD与OA接近平行， 以εp表示塑性应变OD，εe表示弹性应变DC，则B点的应变为：ε＝εe＋εp。如果从D点重新加载，开始时仍沿DB变化，在回到B点后则按BFH变化并产生新的塑性变形。若在B′卸载至D′，则再加载时，B′点的应力成为新的屈服极限，它高于初始屈服极限σ
。这一现象称为应变强化或加工强化。B′点的应力称为后继屈服极限或加载应力。对于均匀应力状态，外载全部卸除后，宏观应力等于零，但保留了宏观的残余应变。实际上，物体内部微观结构发生了变化，产生了微观的残余应力，它能在下次加载时扩大物体的弹性范围。J.包辛格于1886年发现，在卸载后施加反方向压力时，反向屈服极限降低了。这一现象后称为包辛格效应，它是上述微观残余应力造成的。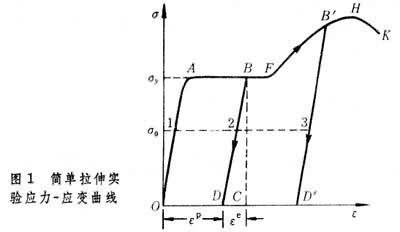
由简单应力状态的应力-应变曲线可以看出，塑性力学问题有两个主要特点：一是应力与应变之间的关系是非线性的；二是应力与应变之间的关系不是单值对应的，而与加载历史有关。例如在图1中，同一应力σ0视加载历史的不同可对应于1、2、3点的应变。 因此塑性力学的问题是从某一已知初始状态开始，随着加载过程，用应力增量与应变增量的关系逐步求出每时刻的增量，累加起来得到物体内的最终应力和应变分布。
②静水压力实验 实验表明，静水压力可使材料的可塑性增加，原来处于脆性状态的材料可以转化成为塑性材料。但静水压力对金属材料的屈服极限影响不大(岩石材料则不同)。平均正应力在几万个大气压以内时，金属材料的体积变化与平均正应力近似成正比。
基本假设 为了简化计算，根据实验结果可以建立如下假设：①材料是各向同性的和连续的，不考虑断裂。②平均正应力不影响材料的屈服，它只与材料的体积应变有关，且体积应变是弹性的。③材料的弹性性质不受塑性变形的影响。④只考虑稳定材料，即不考虑塑性应变的弱化阶段（图1中的HK段）。此外，在一般的塑性静力问题中，还假设时间因素对材料的性质没有影响。变形速度、应变率、应力率等概念往往只表示位移、应变、应力的增量，这些增量在多长时间内产生，对分析问题没有影响。以上假设适用于一般金属材料，对于岩土材料则需考虑平均正应力对屈服的影响以及弹塑性耦合问题。
简化模型 塑性力学的应力－应变曲线通常有如下五种简化模型：
①理想弹塑性模型 对低碳钢或强化性质不明显的材料，若应变不太大，则可忽略强化因素，而将实际应力-应变曲线（图2中虚线）简化为折线，如图2所示，图中0-1线表示理想弹性，1-2线表示理想塑性。
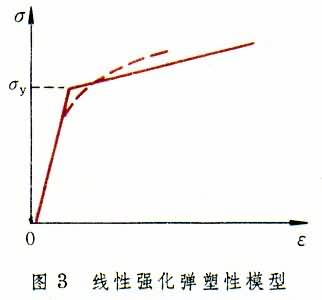
②线性强化弹塑性模型 对有显著强化性质的材料，可用两条直线代替实际曲线 （图3）。
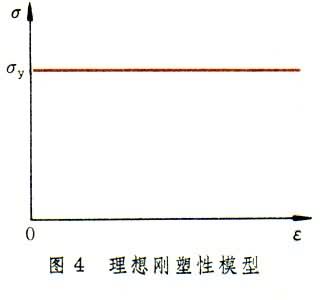
③理想刚塑性模型 对弹性应变比塑性应变小得多而且强化性质不明显的材料，可用水平直线代替实际曲线（图4）。
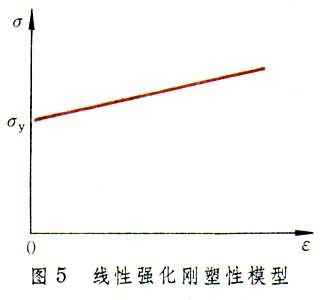
④线性强化刚塑性模型 对弹性应变比塑性应变小得多而且强化性质明显的材料，可用倾斜直线代替实际曲线（图5）。
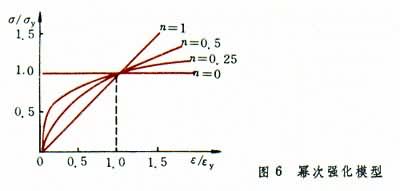
⑤幂次强化模型 为简化计算中的解析式，可用幂次强化模型(图6)，其解析表达式为σ＝σ
(ε/ε)n，其中σ为屈服应力；ε为与σ相应的应变；n为材料常数。屈服条件和本构关系 在复杂应力状态下，各应力分量成不同组合状况的屈服条件以及应力分量和应变分量之间的塑性本构关系是塑性力学的主要研究内容，也是分析塑性力学问题时依据的物理关系。
屈服条件是判断材料处于弹性阶段还是处于塑性阶段的判据。对金属材料，最常用的屈服条件有最大剪应力屈服条件（又称特雷斯卡条件）和弹性形变比能屈服条件(又称米泽斯条件)。这两个屈服条件数值接近，它们的数学表达式都不受静水压力的影响，而且基本符合实验结果。对于理想塑性模型，在经过塑性变形后，屈服条件不变。但如果材料具有强化性质，则屈服条件将随塑性变形的发展而改变，改变后的屈服条件称为后继屈服条件或加载条件（见强化规律）。
反映塑性应力-应变关系的本构关系，一般应以增量形式给出，这是因为塑性力学中需要考虑变形的历程，而增量形式可以反映出变形的历程，反映塑性变形的本质。用增量形式表示塑性本构关系的理论称为塑性增量理论。研究表明，应力和应变的增量关系与屈服条件有关。增量理论的本构关系在理论上是合理的，但应用起来比较麻烦，因为需要积分整个变形路径才能得到最后的结果。因此，在塑性力学中又发展出塑性全量理论，即采用全量形式表示塑性本构关系的理论。在单向应力状态下，若限定应力只增不减（即只加载不卸载），则应力全量与应变全量之间就有直接关系，如同非线性弹性关系那样。在复杂应力状态下，若各应力分量按一定比例增长（称为比例加载）而不卸载，则可将增量关系积分得全量关系。但一般情形下，各应力分量之间的比例是有变化的，严格说来，不能得出全量关系。然而全量关系使用方便，因而常用于求解实际问题。研究表明：在偏离比例加载不大时，全量理论的计算结果和实验接近，至于允许偏离的程度，尚无定量的标准。
解决塑性力学的边值问题，所使用的平衡方程、几何方程（即应变和位移的关系）以及力和位移的边界条件都和弹性力学中所使用的相同，但在物理关系上则应以全量理论或增量理论的塑性本构关系代替弹性力学中的广义胡克定律（见胡克定律）。利用平衡方程、几何方程、物理关系和所有边界条件可以求得超过屈服极限后的应力和应变分布以及内力和外载荷之间的关系。但是塑性力学的本构关系是非线性的，在具体计算边值问题时会遇到一些数学上的困难，因此在塑性力学中还要根据所研究问题的具体情况，找出解决方法。
研究内容 除上述基本理论以外，塑性力学还包括以下研究内容：
简单弹塑性问题 经过简化只剩下一个独立变量的问题。这类问题有：
①梁的弹塑性弯曲问题 如果象处理弹性弯曲问题一样引用平截面假设，则梁的弹塑性弯曲问题就成为一维问题。在弯矩Μ的作用下，梁截面上的正应力分布为σx=Μy/I，其中x为梁纵轴坐标，y为截面上的坐标，y=0对应于中性轴，I为截面绕中性轴的惯性矩。对一个宽为b、高为h的矩形截面梁，I=bh3/12。当最外层纤维的应力达到屈服极限σ
时，作用在截面上的弯矩为弹性极限弯矩Μe=σbh2/6。如果弯矩继续增加，则外层纤维首先进入塑性变形阶段，从梁截面上看，塑性变形区随弯矩的增加向中心发展，纯弹性变形区逐渐缩小。在极限情形，弹性区缩小为零。对于理想塑性材料，与极限情形对应的弯矩称为塑性极限弯矩，其值为Μp=1.5Μe。这一结果意味着，如果允许梁内发生塑性变形，矩形截面梁的抗弯矩能力最多可以提高50％。弯矩达到塑性极限弯矩前，梁的变形仍属弹性量级。因此，在设计中可让梁内发生部分塑性变形以提高梁的承载能力。一般说来，梁的静不定次数（见静不定结构）愈高，承载能力提高的幅度愈大。②受内压厚壁圆筒问题 研究对象是一个内半径为a1，外半径为a2，并且受内压p作用的长厚壁筒。这是一个轴对称问题，可在以筒轴为z轴的柱坐标系(r，θ，z)中进行研究。若考虑轴向应力σz＝0的情形，则壁内的两个主应力为σr（＜0）和σθ（＞0），最大剪应力屈服条件可写成σθ－σr=σ
。根据弹性分析可知，σθ-σr在内壁处最大。当压力p＝σ(a娤－a娝)/2a娤时，内壁开始产生塑性变形。塑性区随着压力的增加而向外扩展。在分析这一问题时，要区分弹性和塑性区，在不同区域中使用不同的应力-应变关系;另外还要求各物理参量（应力、应变等）在弹性区和塑性区的交界面上满足连接条件和初始屈服条件。由这两个条件可定出弹塑性交界面的位置。对于理想塑性材料，当应力满足屈服条件时，材料可无限制地发生塑性变形。但实际上，塑性区的变形受到外层弹性区的约束，不能无限发展，材料处在约束塑性变形阶段。当塑性区扩展到外边界r＝a2处时，外层的弹性约束消失，塑性变形可以自由发展，这时所对应的压力称为塑性极限压力，其值为σln(a2/a1)。若在到达塑性极限压力前卸载，壁内就产生残余应力。再次加载时，应力将从这个残余应力上增长。和简单拉伸时的情形一样，残余应力可使弹性范围提高到卸载前的最高值。利用残余应力的这一特性，可以延长大炮筒及其他压力容器的使用寿命。③长柱体的塑性自由扭转问题 按照弹性力学中解决此类问题的方法引进应力函数Ψ（x，y）（见柱体扭转和弯曲），把不为零的剪应力τzx、τyz表示为：
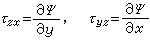，则平衡方程自动满足。最大剪应力τ
＝(τzx2+τyz2)1/2＝|墷Ψ|出现在柱体边界上，式中墷为梯度算符。当扭矩增大到弹性极限时，边界上某些点处|墷Ψ|=τ
，τ为剪切屈服极限，塑性变形首先在那些点产生。随着扭矩的增大，塑性区向内发展。对于理想塑性材料，在塑性区内|墷Ψ|=τ为一常数。另外，从边界条件的要求可知，边界上Ψ＝0。塑性区内的Ψ函数可用边界上的等梯度斜面表示。取柱体的一个截面，当整个截面进入塑性屈服阶段时，那些边界上的斜面汇交成一个在此截面上的沙堆形状包络面，沙堆体积的两倍对应于塑性极限扭矩。这种用沙堆体积计算柱体极限扭矩的方法就称为塑性扭转问题中的沙堆比拟法，通过它可以求得较复杂截面柱的极限弯矩和剪应力分布规律。塑性力学的平面问题 这类问题可分为：
①塑性平面应变问题 金属压力加工中的薄板轧制、拉拔、挤压等问题即属于塑性平面应变问题。这种问题的特点是：应变被限制在一个平面内。这种问题的塑性变形比弹性变形大得多，故可采用刚塑性模型。在土建工程中，边坡稳定问题和长条形地基基础问题等也可作为塑性平面应变问题。塑性平面应变问题有三个方程：两个平衡方程和一个屈服条件方程。如果边界上给定的是应力条件，则可利用三个方程求出应力的分布，而且不需要使用塑性本构关系。在得到问题的解后，应校核刚性区内各点的应力是否满足屈服条件，只有不满足屈服条件，解才算是一个静力允许解；另外，还要校核所得的解给出的位移速度能否满足位移速度的边界条件以及外力在这个位移速度上是否作正功率的条件，如果又满足这些条件，解才是一个完全解。塑性平面应变问题可以用滑移线法求解。对于土力学问题，在平衡方程中，还要考虑重力项。
②塑性平面应力问题 主要出现在薄板中。有塑性变形的薄板中孔洞附近的应力集中问题、圆孔的扩张问题和薄板的弯曲问题等均属塑性平面应力问题。在塑性平面应力问题中，沿厚度z方向的应力等于零。设在板平面内的主应力为σ1、σ2，则屈服条件为max(|σ1-σ2|，|σ1|，|σ2|)=σ
。在应力满足屈服条件时，板中可能产生垂直于板平面的剪切滑动，造成在板平面上看来垂直于滑动方向的速度间断，并会引起厚度变化等复杂问题。塑性极限分析 对于理想塑性材料，当外载荷达到某个极限值时，塑性区的变形不再受约束，材料处于塑性流动状态，即材料可以无限制地变形，这种状态称为塑性极限状态，与此状态对应的载荷称为塑性极限载荷。对物体在塑性极限状态下特性的研究称为塑性极限分析，其主要目的是求出塑性极限载荷，有两种方法：一种方法是，同时考虑弹性变形和塑性变形，求出塑性区的扩展和载荷的关系，最后求得塑性极限载荷；另一种方法是，忽略弹性变形而采用刚塑性模型求出塑性极限载荷。这两种方法所得的结果是相同的。由于第一种方法比较复杂，所以通常采用第二种方法。在用上述两种方法求解复杂问题时，可根据塑性极限分析的上、下限定理（见结构塑性极限分析），对塑性极限载荷作出足够精确的估计。除了求塑性极限载荷外，塑性极限分析还可用于寻找结构在塑性极限状态下的破坏形式，以及用于估计金属塑性成型中的外力和构件的变形。
塑性动力学 研究各种弹塑性体或结构在短时强载荷作用下的应力、变形和运动规律。由于物体有惯性，所以对物体突加强载荷不可能同时扰动物体各部分质点，扰动须经过一个传播过程才能由扰动区逐步传播到未扰动区。外力对于物体的动力效应需要通过分析塑性波的传播来研究，这类问题称为塑性波的传播问题。在实际中，一般都使梁、板、壳等结构在最小尺寸面突然受载，在这种情况下，结构的动力效应主要表现为结构的塑性变形随时间变化，这类问题通常称为结构的塑性动力响应问题。（见塑性动力学）
粘塑性理论 在传统的塑性力学中，并不考虑粘性效应。实验结果表明，金属、土壤或混凝土的粘性效应都很明显。考虑粘性效应才能够解释变形速度变化对塑性变形的影响。最早研究粘塑性体并给出简单力学模型的是E.C.宾厄姆，他的力学模型实际上是理想刚塑性体和牛顿流体的组合。目前粘塑性理论在结构的强度和刚度问题中，在塑性动力学中都有广泛应用。（见粘塑性理论）
结构的塑性稳定性问题 细长杆件或薄壁结构在压力下处于平衡状态，如果受到外界的微小扰动，杆件或结构就可能出现失稳的问题。若失稳前结构处于弹性平衡状态，则属于弹性稳定性问题；若结构已部分或全部处于塑性状态，则属于塑性稳定性问题。随着轻质材料的广泛使用，优化设计的进展，塑性稳定性问题日益增多。在这类问题中平衡的分支点和结构的失稳点并不一致。另外，由于材料在塑性拉伸变形情形下会发生局部的颈缩现象，颈缩处应力的迅速增长也会使结构失稳，这种现象称为拉伸失稳，是进入塑性阶段后所特有的失稳形式。
简史 塑性变形现象发现较早，然而对它进行力学研究，是从1773年C.-A.de库仑提出土的屈服条件开始的。H.特雷斯卡于1864年对金属材料提出了最大剪应力屈服条件。随后A.J.C.B.de圣维南于1870年提出在平面情况下理想刚塑性的应力-应变关系，他假设最大剪应力方向和最大剪应变率方向一致，并解出柱体中发生部分塑性变形的扭转和弯曲问题以及厚壁筒受内压的问题。M.莱维于1871年将塑性应力-应变关系推广到三维情况。1900年J.J.格斯特通过薄管的联合拉伸和内压试验，初步证实最大剪应力屈服条件。此后20年内进行了许多类似实验，提出多种屈服条件，其中最有意义的是R.von米泽斯1913年从数学简化的要求出发提出的屈服条件（后称米泽斯条件）。米泽斯还独立地提出和莱维一致的塑性应力-应变关系（后称为莱维-米泽斯本构关系）。G.I.泰勒于1913年，W.洛德于1926年为探索应力-应变关系所作的实验都证明，莱维-米泽斯本构关系是真实情况的一级近似。为更好地拟合实验结果，A.罗伊斯于1930年在L.普朗特的启示下提出包括弹性应变部分的三维塑性应力-应变关系。至此，塑性增量理论初步建立。但当时增量理论用在解具体问题方面还有不少困难。早在1924年H.亨奇就提出了塑性全量理论，由于便于应用，曾被A.L.纳戴等人，特别是A.A.伊柳辛等苏联学者用来解决大量实际问题。虽然塑性全量理论在理论上不适用于复杂的应力变化历程，但是计算结果却与板的失稳实验结果很接近。为此在1950年前后展开了塑性增量理论和塑性全量理论的辩论，促使从更根本的理论基础上对两种理论进行探讨。另外，在强化规律的研究方面，除等向强化模型外，W.普拉格又提出随动强化等模型。20世纪60年代以后，随着有限元法的发展，提供恰当的本构关系已成为解决问题的关键。所以70年代关于塑性本构关系的研究十分活跃，主要从宏观与微观的结合，从不可逆过程热力学以及从理性力学等方面进行研究。实验研究也集中在求后继屈服面的形状方面。在解题方面则更多注意对大变形的分析。在实验分析方面，也开始运用光塑性法、云纹法、散斑干涉法等能测量大变形的手段。另外，由于出现岩石类材料的塑性力学问题，所以塑性体积应变以及材料的各向异性、非均匀性、弹塑性耦合、应变弱化的非稳定材料等问题正在研究之中。