伯努利数(卷名：数学)
Bernoulli numbers
18世纪瑞士数学家雅各布第一·伯努利引入的一个数。设伯努利数为Bn，其定义:
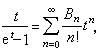这里|t|<2π。由计算知：B0=1，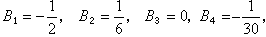
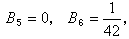
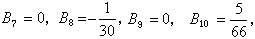
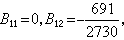
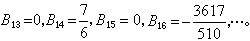一般地，n≥1时，有B2n+1=0;n≥2时，有公式
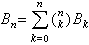可用来逐一计算伯努利数。伯努利数在数论中很有用。例如，对于佩尔方程x2-py2=-4（p呏1(mod4)是素数），N.C.安克尼和E.阿廷曾猜想它的最小解
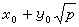满足p凲y0，1960年，L.J.莫德尔证明了在p呏5(mod8)时，S.乔拉证明了在p呏1(mod8)时，上述猜想等价于伯努利数
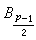的分子不被p整除。伯努利数还可用于费马大定理的论证中。设p>3，如果伯努利数B2，B4，…，Bp-3的每一个的分子不被p整除，这样的素数p叫正规素数，否则就叫非正规素数。德国数学家E.E.库默尔证明了:当p为正规素数时，费马大定理成立。不难计算当3<p<100时，除开p=37，59，67以外，其余的素数都是正规素数。因此，在费马大定理的研究中，库默尔的结果是一项突破性的工作(见不定方程)。尽管有许多判别正规素数的法则，但是，是否有无穷多个正规素数，尚未解决。而非正规素数有无穷多个，早在1915年就被人们所证明。