位势论(卷名：数学)
potential theory
位势的概念来源于物理学中的万有引力理论。因为位势在不分布质量的地方是调和的，所以关于狄利克雷问题的研究一直是位势论中的一个重要内容。由于（G.F.）B.黎曼把位势论和函数论统一处理，以及现代分析的基础理论（如泛函分析、测度论、广义函数、拓扑学等）在位势论中的深入应用，位势论成了数学领域内比较彻底地完成了现代化变革的一个分支。它同黎曼曲面论、偏微分方程、调和分析、概率论等数学分支也有着紧密的联系。
基本概念和主要原理 设Ω是n维(n≥2)欧几里得空间Rn中的一个区域，μ是拉东测度(以下简称测度，若μ是非负的，也用μ≥0表示)，它的支柱S(μ)嶅Ω，K(x，y)是定义在Ω×Ω上的广义实值函数，那么
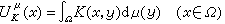称为测度μ 的K位势。K(x，y)则称为位势U
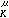(x)的核函数。用|·|表示Rn中的范数，当
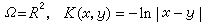时，U
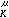(x)称为平面上的对数位势。当Ω=Rn(n≥3)，0<α<n，K(x，y)=|x-y|
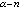时，U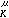
(x)称为μ的α位势（或里斯位势），此时也记作U
(x)。特别α=2时，U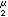
(x)称为μ的牛顿位势。下面限于讨论U
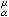扝∞的情形。对Rn里的两个测度μ和v，把
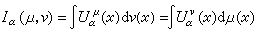称为μ，v的α相互能量。特别称Iα(μ)=Iα(μ，μ)为μ的α能量。把支柱包含在紧集K中且总质量等于1的非负测度全体记作
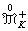，令
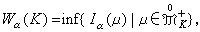则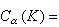
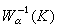称为紧集K的α容量。对任意集合E，把
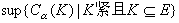称为E的α内容量，把
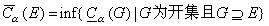称为E的α外容量。若Cα(E)=婔α(E)，则说E是α可定容的。G.绍凯证明了所有解析集，从而所有的波莱尔集是α可定容的。当Cα(E)=0（或婔α(E)=0）时，称E为α内（或外）零容集。一个性质若除了一个α内零容集外处处成立，则说该性质近乎处处成立；若除了一个α 外零容集外处处成立，则说该性质似乎处处成立。对任意零容的紧集K都有v(K)=0的测度v称为C绝对连续测度。
集合E称为α极集，若存在测度μ≥0，其α位势在且仅在E上等于+∞。E是α极集的充要条件是:E为α零容的GΛ集。
对紧集 K，
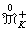关于浑收敛拓扑是紧的，从而存在
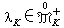使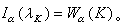
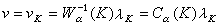称为K的α平衡测度，它满足:
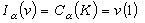(v(1)是v的总质量)。它的位势Uǎ(x)称为K的α平衡位势α它满足：
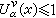在S(v)处处成立而 
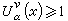在K上近乎处处成立。特别当0<α≤2时，由第一极大值原理知
在Rn处处成立。对任意集E，当Cα(E)<∞（或婔α(E)<∞）时有相应的内(外)平衡测度。当0<α≤2，α<n，若E可定容且Cα(E)<∞时，E的内、外平衡测度相等，称之为E的平衡测度。此时v是满足①支柱在唕，②v(1)=Cα(E)，③在E上似乎处处有
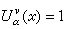诸条件的惟一测度。平衡测度是C绝对连续的，而平衡位势Uǎ(x)是这样一族α位势U
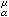(x)的下确界:μ≥0且U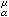(x)≥1在E上似乎处处成立。因此，若μ≥0且
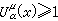在E上似乎处处成立，则μ的总质量μ(1)≥Cα(E)。由于测度的α能量非负，所以能量有限的测度全体在通常的线性组合的意义下，以Iα(μ，v)为内积构成一个实的准希尔伯特空间εα，其中非负测度全体ε
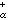是εα的一个完备凸锥。若K紧，那么支柱含于K中的具有限α能量的非负测度全体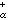ε(K)是ε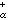的完备凸子锥，因此ε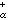的任何元素μ在ε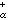(K)上有惟一的正交投影βKμ，即满足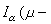
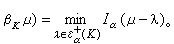当0<α≤2时，βKμ是扫除问题的解，即βKμ满足：
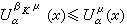在Rn处处成立且等号在K上似乎处处成立。若不假定μ≥0的能量有限，则存在惟一的支柱含于K的测度βKμ使得方程
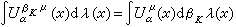对任意λ∈ε
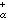成立且βKμ是扫除问题的解。当0<α≤2，α<n时，对α容量有限的波莱尔集E及测度μ≥0，设A是E的紧子集全体以包含关系为序的有向集，则网{βKμ|K∈A}的浑极限βEμ存在，称βEμ为μ到E的扫除测度，扫除测度βEμ是μ到E的扫除问题的解，且扫除位势
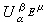是在E上似乎处处满足
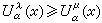的位势族{U
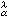(x)}的下确界函数。设εx是在点x的狄喇克测度，则βEεC称为E的α格林测度。对任意测度μ，
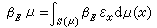。当x0∈唕且
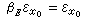时，称x0为E的α正则点，当x0∈唕而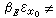
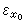时，称x0为E的α非正则点。开集Ω的边界记作дΩ，余集记作CΩ，称
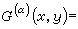
为Ω的α格林函数。以格林函数为核的位势叫做格林位势。当 α=2时，对任意的波莱尔集E吇дΩ，由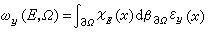
定义的дΩ上的测度ωy称为关于y的调和测度，其中XE表示E的特征函数。当2<α<n时，关于测度的扫除问题一般无解，但J.德尼利用广义函数解决了这个问题。
用ε宎表示单位质量在以y为球心，r为半径的球面的均匀分布。若函数ƒ在Ω里下半连续且满足
①
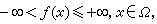
② 对任何x∈Ω，存在正数ρ使对任意正数r<ρ有
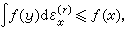则称ƒ在Ω里超调和。不恒等于+∞的超调和函数称为上调和函数。若-ƒ上调和，就说ƒ下调和，既上调和又下调和的函数叫调和函数。当2≤α<n时，α位势U
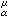(x)是上调和函数。里斯分解定理指出:ƒ在区域Ω里上调和的充要条件是存在惟一的Ω上的测度μ≥0，使得对任何相对紧的区域Ω1嶅捙1嶅Ω有
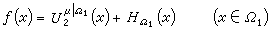，这里μ|Ω1表示μ在Ω1的限制，
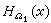在Ω1里调和。当0<α<2时，α位势不是上调和函数。但当U
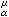(x)是μ几乎处处有限时，它是α上调和函数。一个函数称为α上调和函数，指的是满足下面条件的非负的不恒为+∞的下半连续函数：①
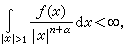
②
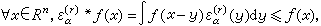式中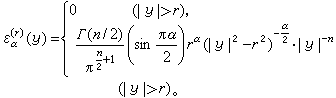 
如果在x0的一个邻域内连续的函数满足条件①且对充分小的r恒有
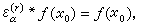则称ƒ(x)在x0是α调和的。若ƒ(x)在集Ω上点点α调和，则称ƒ在Ω里α调和。对于α上调和函数，同样也有类似的里斯分解定理。对上调和函数的连续性的研究导致细拓扑概念的引入。为叙述方便，也称上调和函数为2－上调和函数。用E′表示集E的极限点全体，若x0媂E′或x0∈E′且存在α上调和函数u(x)使
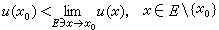成立，则称E在x0是α瘦的。E在x0是α瘦的充要条件是x0媂唕或x0是E的α非正则点。若E的余集在x0为α瘦则说E在x0是α肥的。若E在E的每一点都是α肥的，则说E是一个α肥集。α肥集全体构成Rn里一个拓扑，称为α细拓扑。2-瘦和2-细拓扑通常分别称为瘦和细拓扑。开集必为α肥集，α细拓扑比通常拓扑细。此外，当α<α′时，α细拓扑严格细于α′细拓扑；α细拓扑是使所有α上调和函数（包括α位势）都连续的最粗拓扑。在α细拓扑下的极限叫α细极限。对α细拓扑，α细极限与不相切极限的关系，J.L.杜布等人曾有深入的研究。
第一极大值原理 当0<α≤2，μ≥0时，若U
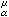(x)≤M，μ几乎处处成立，则该不等式处处成立。当2<α<n时，第一极大值原理不成立。
广义极大值原理 当0<α<n时，若U
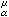(x)≤M在S(μ)上成立，则
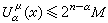处处成立。第二极大值原理 又称控制原理。设μ≥0是能量有限的测度，λ≥0是任意测度，若
μ几乎处处成立，则该不等式处处成立。当0<α<2时，若U
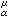(x)关于μ≥0几乎处处有限，ƒ(x)是α上调和函数，且U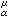(x)≤ƒ(x)，μ几乎处处成立，则该不等式处处成立。惟一性原理 设0<α<n，μ1，μ2是绝对连续的非负测度，若
在S(μ1)∪S(μ2)上似乎处处成立，则μ1=μ2。下包络原理 设0<α≤2，则对任意两个非负测度μ，v存在测度λ，使
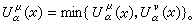
连续性原理 若把U
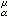(x)看作支柱S(μ)上的函数时是取有限值的连续函数，那么U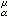(x)在整个空间上也连续。能量原理 对任意测度μ，
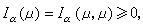等号成立当且仅当μ =0。扫除原理 当0<α≤2时，对任意α容量有限的波莱尔集E和具有限位势的测度μ≥0，扫除问题有解，即存在支柱在唕的测度βEμ使在E上似乎处处有
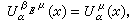且在Rn处处有
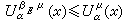。狄利克雷问题 广义形式可叙述为：若Rn的区域Ω的边界дΩ是紧的，对дΩ上的函数ƒ，是否存在惟一的函数u在Ω里调和且对每一个正则边界点y满足：
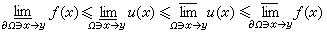且当Ω是无界区域时，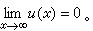
下面采用的佩隆方法是解这个问题的最有效工具，它是历史上有名的施瓦兹交错法及庞加莱扫除法的发展与精密化。
令
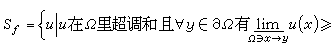
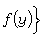（当Ω无界时还要求
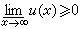），记
那么Hƒ≤啛ƒ。当此式等号成立且仅取有限值时称ƒ是可解的。ƒ可解的充要条件是对于每个x∈Ω，ƒ关于дΩ的调和测度ωx可积分。这时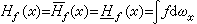 
就是所要求的惟一解。特别，若 ƒ连续则必可解，而且，y∈дΩ为正则边界点的充要条件是对 дΩ上的每个连续函数ƒ有
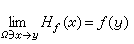。在一定条件下，也可以考虑关于α调和函数的狄利克雷问题。
当0<α≤2，α<n时，y∈дΩ为α正则边界点当且仅当Ω的余集在y是α不瘦的。维纳判别法指出，若0<q<1，令
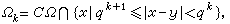则y∈дΩ为α非正则的充要条件是
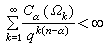，式中Cα(Ωk)表示Ωk的α容量。Ω的α非正则边界点全体是α零容集。此外，关于正则点的充要判别法还可利用闸函数、格林函数、平衡位势等给出，而庞加莱锥判别法是常用的充分判别法。狄利克雷原理 设D0是Rn的有界区域Ω上的连续可微且梯度平方可积的函数全体。在 D0定义内积<
>
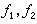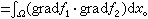记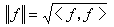
，则依等价关系“～”
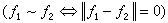得到的商空间 D 是准希尔伯特空间。若ƒ∈D0且有界并可连续地开拓到捙，则狄利克雷问题的解Hƒ满足:
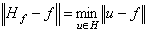，这里H表示D0中的调和函数全体所组成的D的子希尔伯特空间，即Hƒ是ƒ在H上的正交投影。德尼用广义函数证明，D的完备化是由下述BLD函数ƒ组成的：ƒ似乎处处有限且D0中有子列似乎处处收敛于ƒ。若ƒ是有界区域Ω1(叾捙)上的BLD函数，则在Ω上，Hƒ存在且除了一个附加常数外是惟一的使 ‖u-ƒ‖达到极小的BLD函数，也是惟一的在Ω里调和并且可由ƒ开拓成Ω1上的BLD函数的函数。
上述结果都可以推广到ε空间的相对紧的子区域上去。
格林空间与格林函数 连通的豪斯多夫空间Ω若满足下面条件则称之为ε空间:Ω的每一点x有一个开邻域Vx连同一个把Vx变Rn上的一个开子集的同胚y
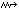Mx(y)，并且任何两个这样的邻域 VC与Vy的交VC∩Vy在相应的两个同胚变换下是保距的（当r≥3）或共形的(当n＝2)。于是作为局部性概念的调和、超调和、上调和函数等可在ε空间Ω上相应地定义。更一般地，也可以用垪n代替上述 Rn来定义ε空间。这种广义ε空间将有若干无穷远点。若ε空间Ω上存在正的非常数的上调和函数，则称Ω为格林空间。例如Rn(n≥3)及Rn的任何有界子区域都是格林空间，R2是ε空间而不是格林空间。格林空间Ω上必存在满足下列条件的函数Gx(y)，称之为以x∈Ω为极的格林函数：①Gx(y)>0；②在Ω\\{x}上，Gx(y)调和；③存在x的邻域V(嶅Vx)使得对每个y∈V，若记y′=Mx(y)，则
式中K为α=2时的核函数，u
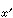调和。由于Gx(y)=Gy(x)，故记作G(x，y)=G(y，x)。
称
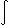G(x，y)dμ(x)(μ≥0)为格林位势。它或恒为+∞，或是个以0为最大调和下属的上调和函数。最一般的抽象边界与CC紧致化 在非空集合Ω上赋予拓扑τ，设I是任一非空号标集，若凬i∈I，Ω的开子集族Bi为Ω的滤基，则I可成为Ω的镶上去的抽象边界，因为在Ω∪I上存在满足下述条件的拓扑τ1：①Ω∈τ1；②τ1在Ω的诱导（相对）拓扑正好是τ；③每个i∈I的邻域系与Ω 的交构成由Bi生成的滤子。这样的拓扑中最细者在I上诱导出离散拓扑；而最粗者当I是Ω上抽象调和函数凸锥的极端母线全体时就称为极小细拓扑。
在实用中，常据在Ω上所考虑的函数族的性质来引入边界且保证Ω镶边后是紧的。康斯坦丁斯库－科尼紧致化定理即若Ω是非紧的局部紧的豪斯多夫空间，φ是一族从Ω到[-∞，+∞]的连续函数，则存在惟一（至多相差一个同胚）的紧空间惂满足：①Ω在惂中是开的且在惂中稠密；②φ中每个函数ƒ能开拓成惂上的连续函数弮;③弮全体能辨别理想边界Δ=惂\\Ω。
惂也可看成关于 Ω上的这样的一致结构的完备化空间:它是使得φ中每个函数都一致连续且相应的一致拓扑与Ω原有拓扑相容的最粗的一致结构。
作为应用，适当选取φ 可以得到如下位势论中常用的紧致化。
亚历山德罗夫单点紧致化 这时φ为空集。
斯通－切赫紧致化 这时φ 是Ω上的所有广义实值连续函数。
凯雷克亚托－斯托伊洛夫紧致化 这时φ 由这样的实值连续函数ƒ组成:在Ω中有紧子集Kƒ使得Ω\\Kƒ是一些区域之并集且在每个区域上ƒ取常数值。
罗伊登紧致化 这时Ω是ε空间，φ 是所有实连续的BLD函数。
倉特善紧致化 这时Ω是ε空间，φ 是满足下述条件的实连续BLD函数ƒ全体：Ω有闭子集Fƒ使得ƒ在Ω\\Fƒ里调和且在那些于Fƒ上取值等于ƒ的BLD函数中，ƒ的狄利克雷积分（即‖ƒ‖D）达到最小。
马丁紧致化 是位势论中重要的一种紧致化。
马丁空间与马丁边界 为纪念R.S.马丁，将格林空间Ω相对于函数族
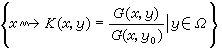（y0∈Ω任意取定）的CC紧致化空间惂 称为马丁空间；Δ＝惂\\Ω称为马丁边界。所有函数xм→K(x，y)(y∈Ω)，在惂都有连续的开拓且能辨别Δ。惂可度量化。Rn的一般区域的欧氏边界与Δ全然不同;但当Ω是球或其他较为正则的区域时，惂等同于Ω的欧氏闭包；对R2的单连通格林区域，Δ等同于卡拉西奥多里分歧边界。调和函数u>0称为极小调和函数，指的是任何不大于u的正调和函数必与u成比例。若u极小调和，必存在x∈Δ使得u(y)=u(y0)·K(x，y)。称这样的X 为Δ的极小点。极小点全体Δ1是 GΛ集。对任一非负调和函数u必存在唯一的分布在Δ1上的拉东测度μ使得凬y∈Ω，
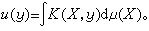称此式为马丁积分表现，其右端是双层位势的推广。它促使了著名的关于凸锥的极端点的绍凯定理的产生并且后者反过来简化了前者的证明。对马丁边界同样可考虑狄利克雷问题，可讨论一个集在X ∈Δ1的瘦与肥并进而把Ω上的细拓扑开拓到Ω∪Δ1。对任意上调和函数u>0及调和函数h>0，u/h在Δ1上至多除去一个h零测集外处处有细极限，这是杜布对著名的法图定理即球内的正调和函数在边界上几乎处处有不相切极限的重大推广。
马丁紧致化有许多推广的形式。例如，当考虑的函数族是由某一椭圆型方程（特别是Δu＝pu）在Ω上的格林函数G′(x，y)的商
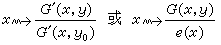（e(x)为确定的有界正解）组成时，可得到椭圆马丁边界Δ′，并进而可研究Ω的椭圆维数，所考虑的方程的解空间的结构以及Δ′与其他边界的关系等。马丁边界可翻译成概率的语言并在随机过程论中得到应用与推广。
局部紧阿贝尔群上位势论 由于拓扑学和代数学，特别是群上傅里叶分析的发展，使这种群上的位势论取得了丰富的成果。
设G是局部紧阿贝尔群，若对G上一个测度网(μα)α∈A，存在一测度μ，使对任意ƒ∈Cc。（支柱紧的连续函数全体），均有
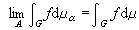，则称(μα)α∈A浑收敛于μ。若G上一正测度集合 ( μt)t>0， 满足以下条件：① μt(G)≤1，t>0;②
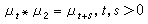，s>0；③
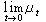浑收敛于狄喇克测度ε0；④浑积分
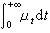存在，则称(μt)t>0是G上一个迁移测度卷积半群。K=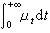称为它所对应的位势核。若测度
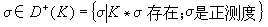，则测度K*σ就称为K位势。一个正测度ξ称为关于(μt)t>0是过度的，若对所有t>0，ξ是μt上调和，即μt*ξ ≤ξ;一个正测度ξ 称为关于(μt)t>0是不变的，若对所有t>0，ξ是μt调和的，也就是μt*ξ=ξ。每一个K位势必为过度测度;反之，每一个过度测度必是单调增加K位势网的浑极限。对过度测度ξ，里斯分解定理成立，也就是ξ=K*σ+η，σ∈D+(K)；η是不变测度。
若
，其中正测度μ 满足μ(G)≤1，μn是n重卷积，μ0＝ε0 则称v为基本核。若K为位势核，则λK+ε0，λ>0，必为基本核。基本核对所有开集满足扫除原理，所以位势核K对所有开集也满足扫除原理。若ω是开集，ξ是过度测度，测度
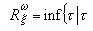是过度测度，在
称为ξ在ω上的简化测度。对简化测度，里斯分解定理仍成立。利用简化测度可证明平衡分布原理和正质量原理；也就是若σ1，σ2∈D +（K），且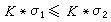
，则有σ1(G)≤σ2(G)。在1978年，还证明了电容器原理，即若ωG是G上哈尔测度，Ω0，Ω1是一对开集 捙0∩捙1=═， 且捙0是紧的，那么存在正测度 μ0，μ1∈D+(K)，使得
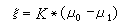满足：①0≤ξ ≤ωG；②ξ =ωG在Ω0；③ξ =0在Ω1；④支柱
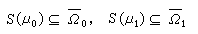。关于位势核K在理想边界的性质，能量有限复测度空间的完备化以及广义函数的引入等，都有了一系列很好的结果。如果把上述迁移测度卷积半群 (μt)t>0所满足的条件①、③放宽为
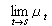浑收敛于μs，t，s>0和μ0=ε0，测度
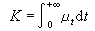就称为亨特核。亨特核满足扫除原理和推广的电容器原理。设x为局部紧豪斯多夫空间，ξ 为x上一个处处稠密正拉东测度（对任意非空开集ω，ξ(ω)>0），由x上一族局部ξ可积的复函数u(x)组成的希尔伯特空间D＝D(x，ξ)，若满足下列三条公理：①对任一紧集K，存在一数A(K)>0，使得
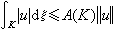;②Cc∩D在D中和Cc中稠密；③对复平面上每一个正常收缩映射T和任一u∈D，有Tu∈D，且‖Tu‖≤‖u‖，则称D(x，ξ)为ξ狄利克雷空间。若对u∈D，存在一拉东测度μ，使得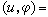
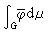，φ∈Cc∩D，则称u为μ的位势。在ξ 狄利克雷空间中，也有相应的电容器原理、平衡分布原理和扫除原理等。公理化位势论 由于位势论的大部分结果都可由其狄利克雷问题、极值原理和收敛性质三个基本原理导出，且为了适应偏微分方程和随机过程的需要，公理化位势论，即调和空间理论迅速地发展起来，它提供了统一处理问题的方法。从50年代起，G.L.陶茨、杜布和M.布雷洛特等在这方面做了开创性的工作，C.康斯坦丁斯库和A.科尼在70年代初期建立了一般调和空间理论。
一般公理系统 又称康斯坦丁斯库－科尼公理系统。在一个局部紧、第二可数的豪斯多夫空间X 的每一开集U上，给出一个由一族不取值－∞的下半连续函数组成的凸锥U(U)，所有这些函数的全体构成x上的一个函数簇U。拓扑空间x上的函数簇是指定义在x的开集上满足下列条件的一个映射U：①对于x的任意开集U，U(U)是U上的函数集；②对于X 的任意开集U，V，U吇V，若ƒ∈U(V)，则ƒ|U∈U(U)；③对于x的任意开集族(Uα)α∈A，一个
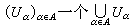上的函数 ƒ，若对一切α ∈A，
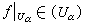，则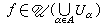
。U称为x上的超调和簇，凸锥U(U)中的函数叫做U上的超调和函数。超调和是局部性质。在一个开集上，一个函数u称为亚调和函数，如果-u是超调和的，若一个函数h既是超调和亦是亚调和，则说h是调和函数。
一个开集U称为可解集，如果在U上超调和函数的极小值原理成立，并且每一ƒ∈Cc(дU)在U内的广义狄利克雷问题是可解的。ƒ的解H
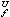在U上可表示为调和测度μ
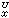的积分
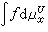，μ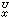
分布在дU上且大于等于零。一般公理系统包括如下四个公理：
正(P)公理 x上的每一点都存在有该点的一个开邻域上的一个调和函数，使它在该点取正值。
可解(R)公理 可解集全体构成拓扑空间x的一个拓扑基。
完备(C)公理 在一个开集U上，任一不取-∞的下半连续函数u若满足在U的每一相对紧的可解子集V(堸嶅U)上，
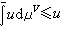，则u∈U(U)。鲍厄收敛(BC)性质 单调增加、局部一致有界的调和函数列的极限仍是调和函数。
满足上述公理的有序偶(x，U)叫做调和空间（或叫CC调和空间）。
布雷洛特公理系统 在一局部紧、第二可数的豪斯多夫空间x上一个调和函数簇H满足如下公理。
① 每一开集U 上的调和函数全体H(U)是C(U)的一个线性子空间。
② 正则区域构成x的一个拓扑基。
所谓正则区域即一个相对紧的区域V，其边界дV上的每一连续函数都可惟一地开拓成为V上的调和函数H抦，并且当ƒ≥0时H抦≥0。
③ 区域上的单调增加的调和函数列的极限是调和函数或恒等于+∞。
有序偶(x，H)叫做布雷洛特调和空间，它是第一个完善的公理系统。布雷洛特调和空间上的位势论与经典位势论最为接近。
此外，比较典型的还有鲍厄-博博克-康斯坦丁斯库-科尼公理系统（简称BBCC公理系统）。二阶椭圆型偏微分方程满足布雷洛特公理系统，但热传导方程却不满足布雷洛特公理系统，而满足BBCC公理系统。一个布雷洛特调和空间是一个BBCC调和空间，而BBCC调和空间是一般的CC调和空间。布雷洛特公理系统严格强于BBCC公理系统，而BBCC公理系统又严格强于一般公理系统。设U是调和空间(x，U)的开子集，u是U上超调和函数，若在U的每一相对紧的可解子集V(堸嶅U)上，
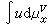是调和函数，则 u叫做上调和函数。-u叫做下调和函数。上、下调和函数在一个稠密集上取有限数值。以 0为最大调和下属的非负上调和函数叫做位势。在调和空间中，相应的里斯分解定理仍然成立。对于布雷洛特调和空间，R.M.埃尔韦证明了，在满足一定条件下，若区域上存在正位势，则格林函数也存在。一个布雷洛特调和空间若存在一个相容的对称格林函数系，称为自共轭调和空间，其原型来自偏微分方程Δu=сu。F.Y.马埃达通过引入梯度测度的概念，在自共轭调和空间上建立了广义格林公式。
位势论与概率论的联系 角谷静夫、卡茨、杜布等人首先发现了布朗运动与古典位势论有密切的联系；亨特则发现通过一大类非常返马尔可夫过程可以深入研究位势论；后来，F.L.斯皮策用随机游动，J.G.凯梅尼和J.L.斯内尔用马尔可夫链首先研究了常返的位势理论。
位势论与概率论的密切联系，最明显的是，决定一个马尔可夫过程的转移函数可以用来定义位势论中的格林函数。位势论中的许多概念和原理都有明确的概率意义，特别体现在上鞅理论中，比如上调和函数相应于上鞅。位势论中的法图型边界极限理论相应于上鞅收敛理论；单调上调和函数列的极限性质与单调上鞅的极限过程性质颇为相似；某些上调和函数、上鞅称为位势，它们在各自的理论中都有与之关联的测度，都遵从只涉及这些测度支柱的控制原理，以及在概率论与位势论中，都存在一个性质相同的简化测度，它导出与位势相关联的测度的扫除等等。
以布朗运动为例，设x(t)，t≥0为Rn上的标准布朗运动，{px}，x∈Rn为相应的概率测度族，px以
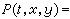
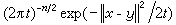为密度，而p(t，x，y)构成强马尔可夫转移半群。令
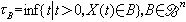（Bn为波莱尔代数），称τB为x(t)首中B的时间，称TB=τ
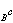为首退出B的时间。若对任意x∈Rn都有px(τB<∞)=0，则说B是极集；若px(τB=0)=1，则说x是B的正则点。对n≥3，令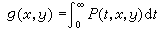
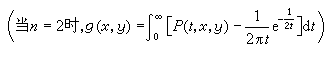，则gμ（μ是拉东测度）就是牛顿位势（当n=2时为对数位势），极集是牛顿零容集。设区域
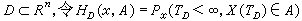，A∈Bn称为布朗运动的退出分布，则HD(x，·)就是D在x点的调和测度。又设φ(x)在дD基本有界，则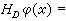
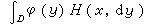就是广义狄利克雷问题的解。令
；
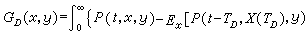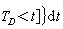则 GD(x，y)就是D上的格林函数。如果u是上调和函数， 在满足一些适当的条件后，u(x(t))是上鞅。在马丁空间也可以构造布朗运动。此外，利用随机积分方程的方法可以构造一般C∞级流形上的扩散过程，因此可以用概率方法研究马丁空间和C∞黎曼流形上的位势论。由于位势论与概率论存在密切的联系，使得位势论有了明显的概率意义而位势论也为概率论的研究提供了一种新的有力的分析工具。
参考书目
N. S. Landkof，Foundations of Modern Potential Theory， Springer-Verlag， Berlin， 1972.
M.Brelot，On Topologies and Boundaries in Potential Theory， Springer-Verlag， Berlin， 1971.
C.Constantinescu and A.Cornea，Potential Theory on harmonic Space，Springer-Verlag， Berlin，1972.
C.Berg and G.Forst，Potential Theory on Locally Compact Abelian Groups，Springer-Verlag， Berlin， 1975.
J.L.Doob，Classical Potential Theory and Its Probabilitic Counterpart， Springer-Verlag， New York， 1984.
M.Tsuji，Potential Theory in Modern Function Theory， Maruzen， Tokyo， 1959.