时间序列分析(卷名：数学)
time series analysis
用随机过程理论和数理统计学方法，研究随机数据序列所遵从的统计规律，以用于解决实际问题。由于在多数问题中，随机数据是依时间先后排成序列的，故称为时间序列。它包括一般统计分析（如自相关分析、谱分析等），统计模型的建立与推断，以及关于随机序列的最优预测、控制和滤波等内容。经典的统计分析都假定数据序列具有独立性，而时间序列分析则着重研究数据序列的相互依赖关系。后者实际上是对离散指标的随机过程的统计分析，所以又可看作是随机过程统计的一个组成部分。例如，用x(t)表示某地区第t个月的降雨量，{x(t)，t=1，2，…}是一时间序列。对t=1，2，…，T，记录到逐月的降雨量数据x(1)，x(2)，…，x(T)，称为长度为T 的样本序列。依此即可使用时间序列分析方法，对未来各月的雨量x(T＋l)(l＝1，2，…)进行预报。时间序列分析在第二次世界大战前就已应用于经济预测。二次大战中和战后，在军事科学、空间科学和工业自动化等部门的应用更加广泛。
就数学方法而言，平稳随机序列（见平稳过程）的统计分析，在理论上的发展比较成熟，从而构成时间序列分析的基础。
频域分析 一个时间序列可看成各种周期扰动的叠加，频域分析就是确定各周期的振动能量的分配，这种分配称为“谱”，或“功率谱”。因此频域分析又称谱分析。谱分析中的一个重要统计量是
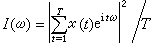，称为序列的周期图。当序列含有确定性的周期分量时，通过I(ω)的极大值点寻找这些分量的周期，是谱分析的重要内容之一。在按月记录的降雨量序列中，序列x(t)就可视为含有以12为周期的确定分量，所以序列x(t)可以表示为
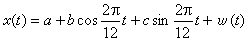，它的周期图I(ω)在
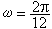处有明显的极大值。当平稳序列的谱分布函数F（λ）具有谱密度ƒ(λ)（即功率谱）时，可用(2π)-1I(λ)去估计ƒ(λ)，它是ƒ(λ)的渐近无偏估计。如欲求ƒ(λ)的相合估计（见点估计），可用I(ω)的适当的平滑值去估计ƒ(λ)，常用的方法为谱窗估计即取ƒ(λ)的估计弮(λ)为
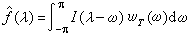，式中wt(ω)称为谱窗函数。谱窗估计是实际应用中的重要方法之一。谱分布F(λ)本身的一种相合估计可由I(ω)的积分直接获得，即
。研究以上各种估计量的统计性质，改进估计方法，是谱分析的重要内容。
时域分析 它的目的在于确定序列在不同时刻取值的相互依赖关系，或者说，确定序列的相关结构。这种结构是用序列的自相关函数
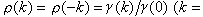0，1，…)来描述的，式中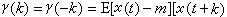
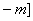为序列的自协方差函数值，m＝Ex(t)是平稳序列的均值。常常采用下列诸式给出m，γ(k)，ρ(k)的估计：
，
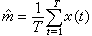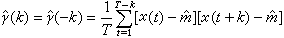
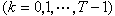
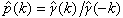
通过
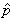(k)了解序列的相关结构，称为自相关分析。研究它们的强、弱相合性及其渐近分布等问题，是相关分析中的基本问题。模型分析 20世纪70年代以来，应用最广泛的时间序列模型是平稳自回归-滑动平均模型 (简称ARMA模型)。其形状为：
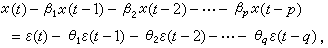式中ε(t)是均值为零、方差为σ2的独立同分布的随机序列;
和σ2为模型的参数，它们满足：
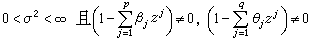对一切|z|≤1的复数z成立。p和q是模型的阶数，为非负整数。特别当q＝0时，上述模型称为自回归模型；当p＝0时， 称为滑动平均模型。根据x(t)的样本值估计这些参数和阶数，就是对这种模型的统计分析的内容。对于满足ARMA模型的平稳序列，其线性最优预测与控制等问题都有较简捷的解决方法，尤其是自回归模型，使用更为方便。G.U.尤尔在1925～1930年间就提出了平稳自回归的概念。1943年，Η.Β.曼和Α.瓦尔德发表了关于这种模型的统计方法及其渐近性质的一些理论结果。一般ARMA模型的统计分析研究，则是20世纪60年代后才发展起来的。特别是关于p，q值的估计及其渐近理论，出现得更晚些。除ARMA模型之外，还有其他的模型分析的研究，其中以线性模型的研究较为成熟，而且都与ARMA模型分析有密切关系。回归分析 如果时间序列x(t)可表示为确定性分量φ(t)与随机性分量ω(t)之和，根据样本值x(1)，x(2)，…，x(T)来估计φ(t)及分析ω(t)的统计规律，属于时间序列分析中的回归分析问题。它与经典回归分析不同的地方是，ω(t)一般不是独立同分布的，因而在此必须涉及较多的随机过程知识。当φ(t)为有限个已知函数的未知线性组合时，即
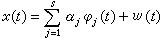，式中ω(t)是均值为零的平稳序列，α1，α2，…，αs是未知参数，φ1(t)，φ2(t)，…，φs(t)是已知的函数，上式称为线性回归模型，它的统计分析已被研究得比较深入。前面叙述的降雨量一例，便可用此类模型描述。回归分析的内容包括:当ω(t)的统计规律已知时，对参数α1，α2，…，αs进行估计，预测x(T +l)之值；当ω(t)的统计规律未知时，既要估计上述参数，又要对ω(t)进行统计分析，如谱分析、模型分析等。在这些内容中，一个重要的课题是:在相当广泛的情况下，证明 α1，α2，…，αs的最小二乘估计，与其线性最小方差无偏估计一样，具有相合性和渐近正态分布性质。最小二乘估计姙j(1≤j≤s)不涉及ω(t)的统计相关结构，是由数据x(1)，x(2)，…，x(T)直接算出，由此还可得
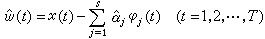对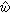
(t)进行时间序列分析中的各种统计分析，以代替对ω(t)的分析。在理论上也已证明，在适当的条件下，这样的替代具有满意的渐近性质。由于ω(t)的真值不能直接量测，这些理论结果显然有重要的实际意义。这方面的研究仍在不断发展。时间序列分析中的最优预测、控制与滤波等方面的内容见平稳过程条。近年来多维时间序列分析的研究有所进展，并应用到工业生产自动化及经济分析中。此外非线性模型统计分析及非参数统计分析等方面也逐渐引起人们的注意。
参考书目
U.Grenander and M. Rosenblatt，Statistical Analysis of Stationary Time Series，John Wiley &Sons， New York，1957.
G.E.P.Box and G.M.Jenkins，Time Series Analysis， Forecasting and Control， Holden-Day，San Francisco， 1970.
E.J.Hannan，Multiple Time Series，John Wiley & Sons，New York，1970.
安鸿志等著：《时间序列的分析与应用》，科学出版社，北京，1983。