不动点算法(卷名：数学)
fixed point algorithm
又称固定点算法。所谓不动点，是指将一个给定的区域A，经某种变换ƒ(x)，映射到A时，使得x=ƒ(x)成立的那种点。最早出现的不动点理论是布劳威尔定理(1912)：设A为Rn中的一紧致凸集， ƒ为将A映射到A的一连续函数，则在A中至少存在一点x，使得x=ƒ（x）。其后，角谷静夫于1941年将此定理推广到点到集映射上去。设对每一x∈A ，ƒ(x)为A的一子集。若ƒ(x)具有性质：对A上的任一收敛序列xi→x0，若 yi∈ƒ(xi)且yi→y0，则有y0∈ƒ(x0)，如此的ƒ(x)称为在A上半连续，角谷静夫定理：设A为Rn中的一紧致凸集，对于任何x∈A，若ƒ(x)为A的一非空凸集，且ƒ(x)在A上为上半连续，则必存在x
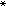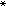∈A，使x∈ƒ(x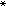)。J.P.绍德尔和J.勒雷又将布劳威尔定理推广到巴拿赫空间。不动点定理在代数方程、微分方程、积分方程、数理经济学等学科中皆有广泛的应用。例如，关于代数方程的基本定理，要证明ƒ(x)=0必有一根，只须证明在适当大的圆│x│≤R 内函数ƒ(x)+x有一不动点即可；在运筹学中，不动点定理的用途至少有二：一为对策论中用来证明非合作对策的平衡点的存在和求出平衡点；一为数学规划中用来寻求数学规划的最优解。对于一个给定的凸规划问题：min{ƒ(x)│gi(x)≤0，i=1，2，…，m}，在此，ƒ和g1，g2，…，gm皆为Rn中的凸函数。通过适当定义一个函数φ，可以证明：若上述问题的可行区域非空，则φ的不动点即为该问题的解。
在1964年以前，所有不动点定理的证明都是存在性的证明，即只证明有此种点存在。1964年，C.E.莱姆基和 J.T.Jr.豪森对双矩阵对策的平衡点提出了一个构造性证明。1967年，H.斯卡夫将此证法应用到数学规划中去。其后，不动点定理的构造性证明有了大的发展和改进。
H.斯卡夫的证明是基于一种所谓本原集，后来的各种发展皆基于某种意义下的三角剖分。现以n 维单纯形Sn为例来说明这一概念，在此，
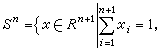
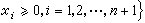。对每一i， 将区间0≤xi≤1依次分为m1，m2…等分，m1<m2<…，mi→
，是给定的一列正整数。对于固定的i，过分点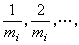
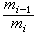依次作平行于xi=0的平面。 这些平面将Sn分成若干同样大小的n维三角形。它们的全体作成的集 Gi，称为Sn的一三角剖分。设ƒ(x)为 Sn→Sn的一连续函数，x＝(x1，x2，…，xn+1)，ƒ（x）=（ƒ1（x），ƒ2（x），…，ƒn+1（x））。定义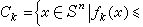
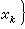。由于ƒ(x)和x皆在Sn上，若有
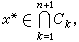则显然有ƒ(x
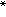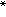)=x，即x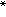为ƒ(x)的一不动点。对每一点y∈Sn赋与标号l(y)=k=min{j│y∈Cj，且yj>0}。由著名的施佩纳引理，在Gi中必存在一三角形σi，它的n+1个顶点yi(k)的标号分别为k(k=1，2，…，n+1)于是可得一列正数ij(j→
)，使得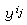
(k)→yk，k=1，2，…，n+1。根据σi的作法，当ij→
时，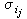
收敛成一个点x
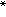。故yk=x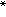，k=1，2，…，n+1。因 
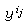(k)的标号为k，故yk∈Ck，因而
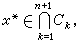即x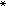
为所求的不动点。因此，求ƒ(x):Sn→Sn 的不动点问题就化为求 σi(i=1，2，…) 的问题。为了计算上的效果，除了上述的标号法之外，还有标准整数标号法、向量标号法等等。关于如何求σi，有变维算法、三明治法、同伦算法、变维重始法等等，通过适当定义，可将上之Sn改为Rn或Rn中之一凸集。求一凸函数在一凸集上的极值问题也可化为求不动点问题。一般说来，这条途径适用于维数不高但问题中出现的函数较为复杂的情况。参考书目
A.J.J.TalmanVariable Dimension Fixed Point Algorithms and Triangulations， Mathematisch Centrum， Amsterdam， 1980.