外推极限法(卷名：数学)
extrapolation to the limit
通过对序列若干项的适当组合来推算序列极限的更精确近似值的方法，简称外推法。
例如，计算圆周率π，即直径为1的圆的周长时，利用外推极限法，只要通过对上述圆的内接正二、三、四、六、八边形等五个正多边形的周长的计算（圆内接正二边形的周长等于直径的二倍），即可得出π的接近9位有效数字的近似值T孈=3.141592648。计算过程如下面形式：
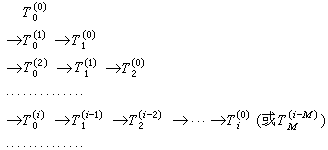其中
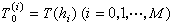，表示第i+1个正多边形的周长，其边数为
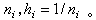而计算过程可用公式表达为
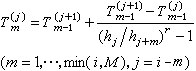(1)式中M=4，r=2。算法(1)的推导利用了正n边形周长T(h)
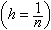的展开式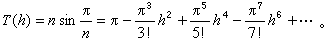
一般情形下，设T(h)是一个问题的近似解，当h→0时，它的极限为τ0，T(h)具有展开式
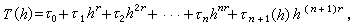式中τ1，τ2，…，τn为常数，τn+1(h)对h有界，那么都可应用算法（1），通过已算出的值T
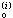=T(hi)(hi≠0，i=0，1，…)来推算τ0的更精确的近似值。这种算法的思想，是通过T(hi)，T(hi+1)，…，T(hi+m)的线性组合，消去τ0的近似b值T(h)展开式中所含hr的低次误差项，使得
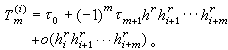
这一方法的实质，是用满足插值条件
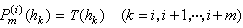的多项式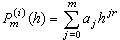
来代替T(h)，用
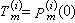来近似表示τ0的值，因此它又称作多项式外推法。如将插值多项式p嫑(h)改为其他插值函数，则得到其他的外推法，诸如有理式外推法、ε算法等。
外推极限法广泛地应用于数值积分、微分方程和积分方程求解等方面。
参考书目
邓建中著：《外推法及其应用》，上海科学技术出版社，上海，1984。