数值稳定性(卷名:数学)
numerical stability
算法对舍入误差的敏感性。在算法执行过程中会出现舍入误差的积累。对同一个计算问题,在不同的算法中舍入误差对计算结果产生的影响也各不相同。舍入误差对计算结果的精确性影响小的算法,具有较好的数值稳定性;反之,算法的数值稳定性差。例如,若干个正数相加时,按从大到小的次序进行就不如按从小到大的次序进行的数值稳定性好。二次方程αx2+bx+с=0求根的公式为:
 (1)
(1) (2)若b>0,且b2>>4|αс|,则由于b和
(2)若b>0,且b2>>4|αс|,则由于b和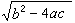 很接近,用公式(1)计算 x1就会使有效数字严重损失。但这时可先用公式(2)计算x2,然后根据关系x1x2=с/α计算x1,会得到比较好的结果。在用消去法解线性代数方程组时,选主元的算法比不选主元的算法的数值稳定性好。
很接近,用公式(1)计算 x1就会使有效数字严重损失。但这时可先用公式(2)计算x2,然后根据关系x1x2=с/α计算x1,会得到比较好的结果。在用消去法解线性代数方程组时,选主元的算法比不选主元的算法的数值稳定性好。算法的数值稳定性的判别是和(舍入)误差分析密切相关联的。早在1947年J.冯·诺伊曼和戈尔茨坦关于高斯消去法舍入误差分析的文章中就隐含着数值稳定性的概念,而首先明确提出这个概念的是J.W.吉文斯。J.H.威尔金森系统地发展了吉文斯提出的向后误差分析的思想,对代数求解过程的舍入误差作了深入细致的分析,计算结果的精度不但依赖于所用的算法,而且也和问题是良态或病态有关。一个计算问题,如果其中的参数(如线性代数方程组的系数,自由项)的微小扰动只对解的精度产生不大的影响,便说这个计算问题是良态的,否则便称为病态的。吉文斯的数值稳定性概念就考虑到问题是良态或病态这个因素。一个算法计算得到的近似解可以看作原计算问题中的参数经适当扰动后的准确解,若扰动是微小的,就说这个算法是数值稳定的,否则就说算法是不稳定的。
参考书目
J. H.Wilkinson,Rounding Errors in Algebrαic Processes,Printice-Hall, Englewood Cliffs, New Jersey, 1963.