数的几何(卷名：数学)
geometry of number
又称几何数论，应用几何方法研究某些数论问题的一个数论分支。它的一类典型问题为：设 ƒ(x1，x2，…，xn)是实变量x1，x2， …， xn的实值函数，对于适当选取的整数u1，u2，…un，｜ƒ(u1，u2，…un)｜的值能有多小？例如，设
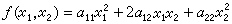是一个正定二次型，用数的几何方法可以证明，存在不全为零的整数u1，u2，使得
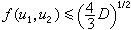，这是最佳结果，其中
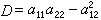是型的判别式。17～18世纪间，J.-L.拉格朗日和C.F.高斯等就已开始以几何观点研究二次型的算术性质。1891年，H.闵科夫斯基发表了数的几何第一篇论文，并于1896年出版了《数的几何学》一书。从此，数的几何成为数论的一个独立分支。
数的几何是研究丢番图逼近、代数数论的重要工具。
用Rn表示n维实欧几里得空间，如果
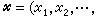
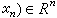的所有坐标都是整数，那么尣称为一个(n维)整点或格点。全体n维整点的集合记作Λ0。设点集
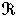嶅Rn，λ是一个实数，把所有形如
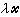(尣∈
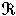)的点组成的集记为
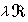。如果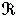
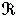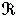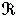=-，亦即若尣∈，则-尣∈，那么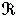称为关于原点对称，或简称为对称。如果当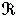含有尣、у时必含有连接尣、у的线段，亦即含有一切形如(1-θ)尣+θу(0≤θ≤1)的点，则称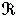为凸集。关于原点对称的凸集，称为对称凸集。一个重要的对称凸集，是由以下的一组实线性型定义的：
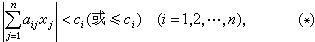式中с1，с2，…，сn是正实数，det(αij)≠0。这是一个有界集，其体积是
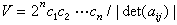。如果(*)中全是“≤”，那么它就定义了一个闭集。闵科夫斯基研究了对称凸集的基本性质，获得数的几何第一基本定理：如果
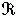嶅Rn是体积为V(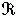)（可能为无穷）的对称凸集，且V()≥2n， 那么在中或其边界上必有一个非零整点。这个定理应用于集(A)，得到著名的闵科夫斯基线性型定理：如果正实数с1，с2，…，сn适合с1с2 … сn≥｜det(αij)｜，那么存在不同时为零的整数x1，x2，…，xn，满足不等式组
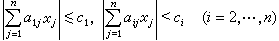。由此定理可以导出丢番图逼近的一系列结果。例如，对于n个实数α1，α2，…，αn，若其中至少有一个无理数，则有无穷多组(p1/q，p2/q，…，pn/q)适合
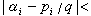
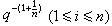。此外，上述定理还可用于解决代数数域的基数问题。有时，需要考虑
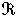中含有多少个线性无关的整点。设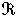是闭的对称凸集，0<V(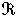)<∞。对于尣∈Rn，定义距离函数
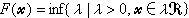，若右式不存在，则令F(尣)=∞。于是0≤F(尣)≤∞，F(λ尣)=λF(尣)(当λ>0)，并且
={尣｜F(尣)≤λ}(λ≥0)。对于集(A)（其中全取“≤”），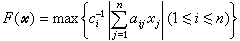
。由F(尣)的性质可知，对每个i(1≤i≤n，存在最小的λ=λj，使
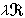含有i个线性无关的整点。λj称为
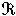的第i个相继极小，亦即
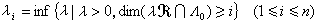，于是存在整点m1，m2，…，mn适合
，
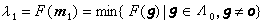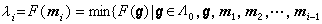线性无关｝(i≥2)。例如，对于超立方体｜xj｜≤1(1≤i≤n)，λj=1(i=1，2，…，n)，mj可取作单位矢(0，…，0，1，0，…，0)。
显然，
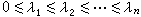，由闵科夫斯基关于数的几何第一基本定理可知，
。闵科夫斯基进而得到数的几何第二基本定理：设
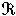是闭的对称凸集，0<V(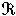)<∞，则其相继极小λ1，λ2，…，λn适合不等式
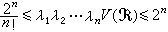。这个定理在数论中有不少有趣而重要的应用，例如，W.M.施密特用它为主要工具解决了实代数数联立有理逼近问题。
参考书目
J.W.S.Cassels，An Introduction to the Geometry of Number，Springer-Verlag，Berlin，1959.