多复变函数论(卷名:数学)
theory of analytic functions of several variables
数学中研究多个复变量的全纯函数的性质和结构的分支学科,有时也称多复分析。它形成较晚,但发展迅速。它虽然有着经典的单复变函数的渊源,但由于其特有的困难和复杂性,在研究的重点和方法上,都和单复变函数论(见复变函数论)有显著的区别。因为多复变全纯函数的性质在很大程度上由定义区域的几何和拓扑性质所制约,因此,其研究的重点经历了一个由局部性质到整体性质的逐步的转移。它广泛地使用着微分几何学、代数几何、李群、拓扑学、微分方程等相邻学科中的概念和方法,不断地开辟前进的道路,更新和拓展研究的内容和领域。如果说各学科的相互渗透和影响日益广泛是近代数学的特征,那么对多复变函数论而言,这一特点尤为显著。
历史发展 多复变函数论的研究,早在单复变函数论的(G.F.)B.黎曼和K.(T.W.)外尔斯特拉斯时代就已经零散地开始了。但真正标志着多复变函数论这一学科创立的,是19世纪末和20世纪初(J.-)H.庞加莱、P.库辛、F.M.哈托格斯等人的工作。他们的研究揭示了多复变全纯函数本质上的独特性。在这当中,库辛提出的关于全纯函数整体性质的两个以他命名的问题以及E.E.列维提出的拟凸域和全纯域是否等价的问题,更有着深远的影响,长时间成为多复变函数论发展的一个推动因素。20世纪30年代以前,虽然出现过K.莱因哈特关于解析自同构群、S.伯格曼关于核函数和度量等重要工作,但整个说来,多复变函数论处于相对沉寂的时期。从30年代开始,多复变的研究迎来了初步繁荣。这一时期中陆续出现了H.嘉当关于全纯自同构的惟一性定理、有界域全纯自同构群的李群性质以及全纯域与全纯凸的等价性的嘉当-苏伦定理等突出成果。特别是从1936年开始,日本数学家岡潔对库辛问题、列维问题、逼近问题等多复变的中心问题进行了长期、系统而富有成效的研究,终于在50年代对上述诸问题给出了解答。他的这一系列工作对以后年代的多复变的发展有着重大的影响。50年代以后,和近代数学的综合化、抽象化的总潮流相一致,在多复变函数论中用拓扑方法和几何方法研究全纯函数的整体性质的趋势变得越来越明显。由J.勒雷引进拓扑学的层及其上同调的概念被迅速而成功地用于多复变。这一概念和H.嘉当早先关于全纯函数理想论的研究以及岡潔的思想结合,导致了凝聚解析层理论的建立。与此同时,复空间和施泰因流形的概念也应运而生。H.嘉当和J.P.塞尔系统地应用凝聚层理论建立了施泰因流形的基本定理。此后不久,H.格劳尔特解决了复流形的列维问题,他和R.雷默特、施泰因等人还大大发展了复空间的理论。整个50年代无疑是多复变发展的黄金时代。
另一方面,近代微分几何与复分析的相互溶合也在不断加快步伐。1913年,(C.H.)H.外尔的黎曼曲面理论导致了复流形概念的建立。É.(-J.)嘉当的外微分式与拓扑的结合产生了G.- W.德·拉姆的上同调理论。以此为基础,W.V.D.霍奇将黎曼曲面上的调和函数理论推广到高维的紧致复流形,证明了紧复流形的基本定理──霍奇定理。40年代以后,与微分几何中的博赫纳技巧相结合,霍奇理论又由小平邦彦所发展和完善。60年代,博赫纳-小平邦彦方法又进而推广到非紧的带边界的复流形,发展成为近代多复分析的一个有力工具:扺问题的L2估计。
多复变函数论中具有重要意义的第三方面进展是C.L.西格尔在1935~1950年间建立的多复变函数的自守函数论。50年代以后,由于A.赛尔伯格、R.朗兰兹、И.М.盖尔范德等人的工作,揭示了它与代数数论、李群的无穷维表示、代数几何等众多学科的内在联系,而日益成为目前极为活跃而且引人注目的近代数学领域之一。
多复变数的全纯函数 以Cn表示n维复欧氏空间,其中的点
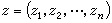 ,每一zi是一复数。设Ω是Cn中的一个开集,复值函数ƒ(z)称为在Ω上是全纯的,如果下列条件满足:对于Ω中的任何点
,每一zi是一复数。设Ω是Cn中的一个开集,复值函数ƒ(z)称为在Ω上是全纯的,如果下列条件满足:对于Ω中的任何点 ,
,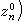 ƒ(z)在z0附近可以表为下述形式的收敛幂级数:
ƒ(z)在z0附近可以表为下述形式的收敛幂级数: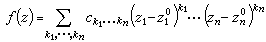 。从形式上看,多复变全纯函数是单复变全纯函数的推广。事实上两者的基本性质确有许多相似之处。例如:
。从形式上看,多复变全纯函数是单复变全纯函数的推广。事实上两者的基本性质确有许多相似之处。例如:① 对每个分量满足柯西-黎曼方程,即
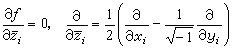 ,
,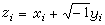 。
。② 惟一性定理 如果ƒ 和g是在区域Ω(连通开集称为区域)上定义的两全纯函数, 并在某一点的邻域有ƒ(z)=g(z),那么在整个Ω上ƒ(z)和g(z)恒等。
③ 极大模原理 设ƒ是在区域Ω上定义的全纯函数,如果在某一内点α,对于所有的z∈Ω,|ƒ(α)|≥|ƒ(z)|成立,那么ƒ(z)恒为常数。
当然,构成多复变数全纯函数研究内容的主要不是这些共同的性质,而是它的独特性质。这方面,下述两个问题具有特别的重要性,它们都导致了长期而且大量的研究:
① 解析开拓 F.M.哈托格斯发现,设Ω是Cn(n≥2)中一个域,K是Ω中紧集,Ω-K连通,那么任何在Ω-K全纯的函数都可以开拓到整个Ω,成为Ω上的全纯函数。这种性质是单复变全纯函数所决不具有的。与这种哈托格斯现象有关的研究构成了多复变函数论的基本内容之一。
② 零点的局部性状 单复变中全纯函数的零点是孤立的。多复变全纯函数的零点,即使以最简单的例子ƒ=z1·z2来看也已经不再是孤立的。有限个全纯函数的公共零点的集合称为解析集。解析集的结构及多复变全纯函数在其零点附近的性状较之单复变的相应情况要复杂得多。讨论这一理论的基础是外尔斯特拉斯预备定理。记Cn的原点为O,以θn表示所有在O的某一邻域全纯的函数组成的环。则外尔斯特拉斯预备定理断言:任何一个非零元ƒ∈θn,都存在一组坐标(z1,z2,…,zn)以O为原点,使ƒ(0,0,…,0,zn)≠0,并且ƒ等于θn中一个可逆元与一个示性多项式的乘积,这里的示性多项式形状为:
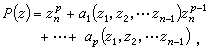 式中
式中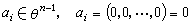 。
。这一定理的作用在于在一定程度上将全纯函数的问题化归多项式的问题。从它出发可以证明,θn是诺特环(即其中的任何理想都具有限基)。不仅如此,著名的对多项式环而言的希尔伯特零点定理对环θn也成立,由此可以获得对解析集局部结构的较清晰的了解。利用这些结果,如果把θn看成Cn上全纯函数的芽生成的层,岡潔证明了多复变函数论中具基本重要性的定理之一:θn是凝聚层。
全纯域与列维问题 如果Ω是复平面C 中的一个域,掍是另一个包含Ω而较大的域,那么总是存在在Ω中全纯而不能全纯开拓到掍的函数(只要任取在掍中而不在Ω的一点α,考虑函数1/z-α即可)。这种现象在多复变函数中不再成立。
哈托格斯发现,Cn中有些域Ω具有这样的性质:总是存在一个包含它的更大的域掍,使任何在Ω中全纯的函数都可以全纯开拓到掍中去。由此,自然提出这样的问题:如何刻画那些不具备以上开拓性质的域?这一问题的精确提法就是全纯域的概念。域Ω嶅Cn称为全纯域,如果不存在更大的包含Ω的域掍,使任何Ω上的全纯函数都可以全纯开拓到掍上。
全纯域的刻画在多复变函数论的历史发展中长时期处于主导的地位。这方面的第一个重要结果是H.嘉当和苏伦给出的:Ω是全纯域的充分必要条件是,对于Ω中的任何紧子集K,集合
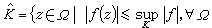 上的全纯函数
上的全纯函数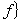 也是Ω中的紧子集。这种性质称为全纯凸性。嘉当-苏伦定理是用全纯凸来刻画全纯域,但更自然的是能给出域的几何刻画。进一步的研究表明,域的全纯性和它的某种凸性有关,在这点上,通常的欧氏空间中的凸域具有一定的借鉴作用。欧氏空间Rn中的凸域(一域称为凸的,如果连接其中任何两点的线段也整个在该域之中),其充要条件是该域上存在一个二阶连续可微的函数u,满足:当x→域的边界时,u(x)→
也是Ω中的紧子集。这种性质称为全纯凸性。嘉当-苏伦定理是用全纯凸来刻画全纯域,但更自然的是能给出域的几何刻画。进一步的研究表明,域的全纯性和它的某种凸性有关,在这点上,通常的欧氏空间中的凸域具有一定的借鉴作用。欧氏空间Rn中的凸域(一域称为凸的,如果连接其中任何两点的线段也整个在该域之中),其充要条件是该域上存在一个二阶连续可微的函数u,满足:当x→域的边界时,u(x)→ ;并且对任何实数λ1,λ2,…,λn,有
;并且对任何实数λ1,λ2,…,λn,有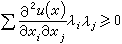 。以此为背景,哈托格斯与列维引进了拟凸域的概念。为了说明这一概念,称定义于Ω上的二阶连续可微的函数u(z)是穷竭的,如果当 z→边界时,u(z)→
。以此为背景,哈托格斯与列维引进了拟凸域的概念。为了说明这一概念,称定义于Ω上的二阶连续可微的函数u(z)是穷竭的,如果当 z→边界时,u(z)→ ;u(z)是多重次调和的,如果对于任何复数λ1,λ2,…,λn,它在Ω中任意点都满足
;u(z)是多重次调和的,如果对于任何复数λ1,λ2,…,λn,它在Ω中任意点都满足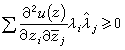 。于是有定义:具有穷竭的多重次调和函数的域,称为拟凸域。
。于是有定义:具有穷竭的多重次调和函数的域,称为拟凸域。根据嘉当-苏伦定理,不难证明全纯域是拟凸域。困难的、长期未决的是其反面:拟凸域是否一定是全纯域?这就是所谓列维问题。列维问题的肯定性解答当n=2时由岡潔最先给出(1942),其一般情况分别由岡潔、伯格曼和F.诺盖独立证明(1953~1954)。列维问题的解决引出了大量的,至今仍很活跃的推广性研究。其中,最具重要性的是格劳尔特的工作。它涉及的是对复流形而言的列维问题。全纯域在复流形中的类似概念称为施泰因流形。简单地说,施泰因流形是这样的复流形:它是全纯凸的,它上面具有足够多的全纯函数以致可以区别不同的点,并给出每一点的局部坐标。于是,对复流形而言的列维问题就变成了:什么样的复流形是施泰因流形 ?格劳尔特对此的回答(1958)是:容许光滑的、穷竭的强多次调和函数存在的复流形是施泰因流形。
解决列维问题的另一种方法是扺算子的L2估计,它在60年代中期得到了迅速的发展。事实上,包括列维问题在内的许多函数论问题,如下面要提到的库辛问题与龙格型定理及复向量丛上的嘉当定理等,都可以化归为扺问题:证明一般的(即可能是非齐次的)柯西-黎曼方程扺u=α(满足条件扺α=0)解的存在性与正则性。从一般的柯西-黎曼方程,自然地得出由(p,q)微分形式的希尔伯特空间到(p,q+1)微分形式的希尔伯特空间的微分算子,即扺算子。它及它的共轭算子扺
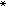 都是线性的稠定的闭算子。1950年,D.C.斯潘塞在企图将霍奇理论推广到开流形时,首先提出了著名的扺-纽曼问题:证明方程
都是线性的稠定的闭算子。1950年,D.C.斯潘塞在企图将霍奇理论推广到开流形时,首先提出了著名的扺-纽曼问题:证明方程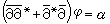 的解的存在性与正则性。这是研究扺问题十分有效的手段。因为若加上条件扺α=0,在知道了这个方程的解φ以后,就可以将扺问题的解表示成u=扺
的解的存在性与正则性。这是研究扺问题十分有效的手段。因为若加上条件扺α=0,在知道了这个方程的解φ以后,就可以将扺问题的解表示成u=扺 φ。通过一系列先验估计,J.J.科恩从1963年开始,对于几类重要的拟凸流形,特别是强拟凸流形,彻底解决了扺-纽曼问题。1965年,L.赫尔曼德尔在微分形式的希尔伯特空间引入权函数来直接研究扺问题,取得了很大成功。权函数的引入避开了扺-纽曼问题中处理解的边界正则性的难点,使得对于一般的施泰因流形直接得到了内部存在性与正则性。因此在某种意义上,它比 扺-纽曼问题更适于多复变函数论的应用。同时,扺算子理论的发展,不仅为复流形,特别是施泰因流形的研究提供了强有力的工具,而且促进了拟微分算子理论的诞生及超定微分方程等分支的发展。
φ。通过一系列先验估计,J.J.科恩从1963年开始,对于几类重要的拟凸流形,特别是强拟凸流形,彻底解决了扺-纽曼问题。1965年,L.赫尔曼德尔在微分形式的希尔伯特空间引入权函数来直接研究扺问题,取得了很大成功。权函数的引入避开了扺-纽曼问题中处理解的边界正则性的难点,使得对于一般的施泰因流形直接得到了内部存在性与正则性。因此在某种意义上,它比 扺-纽曼问题更适于多复变函数论的应用。同时,扺算子理论的发展,不仅为复流形,特别是施泰因流形的研究提供了强有力的工具,而且促进了拟微分算子理论的诞生及超定微分方程等分支的发展。库辛问题与龙格型定理 推动多复变函数论发展的内在逻辑之一是寻求单复变函数论中的哪些基本事实可以推广到多复变中来。还在多复变发展的早期,法国数学家库辛就提出了单复变中两个经典定理(外尔斯特拉斯定理和米塔-列夫勒定理)如何推广的问题,这就是库辛问题。单复变中的外尔斯特拉斯定理是说,对C中域Ω而言,永远存在这样的全纯函数,它以指定的点集(当然假定是离散的)为自己的零点集,并且重数等于指定的重数。米塔-列夫勒定理说,对C中域Ω而言,永远存在这样的亚纯函数,它以指定的点集为自己的极点集,并且重数等于指定的重数。为了说明库辛问题,先解释什么是多复变的亚纯函数。定义于区域中的复值函数如果它在任何点的局部都可以表为两个全纯函数之商并且分母不恒为零,这样的函数称为亚纯函数。库辛第一问题:{Uα}是区域Ω的一组开集覆盖,对每一α,有一定义于Uα的亚纯函数ƒα满足,当
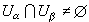 时,ƒα-ƒβ是Uα∩Uβ上的全纯函数(换言之,ƒα和ƒβ在定义域相交的部分有相同的极点)。是否存在整个定义于Ω的亚纯函数ƒ,使对每一α,ƒ-ƒα在Uα上是全纯的?库辛第二问题:设{Uα}是域Ω的开集覆盖。如果对每一Uα,有一定义于其中的全纯函数ƒα满足,如
时,ƒα-ƒβ是Uα∩Uβ上的全纯函数(换言之,ƒα和ƒβ在定义域相交的部分有相同的极点)。是否存在整个定义于Ω的亚纯函数ƒ,使对每一α,ƒ-ƒα在Uα上是全纯的?库辛第二问题:设{Uα}是域Ω的开集覆盖。如果对每一Uα,有一定义于其中的全纯函数ƒα满足,如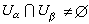 ,
,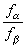 是Uα∩Uβ上不取零值的全纯函数(即ƒα和ƒβ在定义域相交的部分有相同的零点)。是否存在一个整体定义于Ω的全纯函数ƒ,使对每一α,ƒ/ƒα在Uα上为一不取零值的全纯函数?对库辛问题的解决作出最主要贡献的是岡潔。它们的解决一方面与全纯域的理论有关,一方面与层及层的上同调理论有关。岡潔对库辛问题的解答如下:如果Ω是全纯域,库辛第一问题是永远可解的。但即使是全纯域,库辛第二问题并不一定永远可解,它的可解性还依赖于一定的拓扑条件。其可解的一个充分必要条件是,它在连续函数的范畴内可解,即如果能找到一个定义于Ω的连续函数g,使对每一α,
是Uα∩Uβ上不取零值的全纯函数(即ƒα和ƒβ在定义域相交的部分有相同的零点)。是否存在一个整体定义于Ω的全纯函数ƒ,使对每一α,ƒ/ƒα在Uα上为一不取零值的全纯函数?对库辛问题的解决作出最主要贡献的是岡潔。它们的解决一方面与全纯域的理论有关,一方面与层及层的上同调理论有关。岡潔对库辛问题的解答如下:如果Ω是全纯域,库辛第一问题是永远可解的。但即使是全纯域,库辛第二问题并不一定永远可解,它的可解性还依赖于一定的拓扑条件。其可解的一个充分必要条件是,它在连续函数的范畴内可解,即如果能找到一个定义于Ω的连续函数g,使对每一α,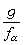 在Uα上为一不取零值的连续函数。上述对库辛问题的解答揭示了一个在多复变研究中具有指导性的哲理:许多涉及全纯性范畴的问题的可解性常常依赖于连续性范畴的相应问题的可解性,虽然这并不是业已证明的原理,但却是经常有效的。
在Uα上为一不取零值的连续函数。上述对库辛问题的解答揭示了一个在多复变研究中具有指导性的哲理:许多涉及全纯性范畴的问题的可解性常常依赖于连续性范畴的相应问题的可解性,虽然这并不是业已证明的原理,但却是经常有效的。龙格型定理研究的是全纯函数的逼近。单复变中最简单的龙格定理如下:如K是复平面C中一个有界闭集,ƒ是一定义于K的某邻域的全纯函数,那么ƒ一定可以用多项式一致逼近。注意到多项式可以一致逼近任意整函数,而整函数就是定义于C的全体全纯函数。因此多复变中的龙格定理的正确提法应该是:如果Ω是全纯域,K是Ω中的有界闭集,并且
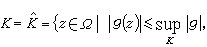 凬Ω中全纯函数g}如果ƒ 是定义于K 的某邻域的全纯函数,那么ƒ一定可以用定义于Ω的全纯函数一致逼近。这种类型的龙格定理是由A.韦伊及岡潔证明的。
凬Ω中全纯函数g}如果ƒ 是定义于K 的某邻域的全纯函数,那么ƒ一定可以用定义于Ω的全纯函数一致逼近。这种类型的龙格定理是由A.韦伊及岡潔证明的。复流形和复向量丛 正如单复变全纯函数的研究必然导致黎曼曲面的概念一样,在多复变中复流形的引进同样是不可避免的。粗略地说,复流形是这样的拓扑空间,其每点的局部和Cn中的开集相同。精确地说,满足以下条件的拓扑空间M称为n维复流形:M是一个豪斯多夫拓扑空间。{Uk}是M的一族开集覆盖。对每一k,存在Uk与Cn中某开集Ωk的一个双方一一的连续映射φk,满足:①M的每一点都至少属于一个Uk,②如果
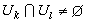 ,则映射
,则映射 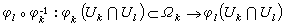
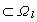 是全纯的。在这种定义下,可以将M中的Uk和Cn中的Ωk等同起来,而将Ωk中点的坐标称为Uk中相应点的局部坐标,于是条件②表明,不同局部坐标之间的关系是全纯的。由此可推知,定义于M上的复值函数如果对某一局部坐标是全纯的,那么对任何其他局部坐标也都是全纯的。因此,复流形上全纯函数的定义是有意义的。
是全纯的。在这种定义下,可以将M中的Uk和Cn中的Ωk等同起来,而将Ωk中点的坐标称为Uk中相应点的局部坐标,于是条件②表明,不同局部坐标之间的关系是全纯的。由此可推知,定义于M上的复值函数如果对某一局部坐标是全纯的,那么对任何其他局部坐标也都是全纯的。因此,复流形上全纯函数的定义是有意义的。复流形按其是否紧致,分为紧复流形和非紧复流形两大类。相对地说,紧复流形的研究成果要丰富得多。复流形的各方面:几何、拓扑、函数论及其相互关系都各有独自而又相互交叉的研究,构成了近年来蓬勃兴起的新分支大范围分析(见大范围变分法)的重要内容之一。
在多复变函数论中研究得最深入的非紧复流形是施泰因流形。设有复流形M,满足条件:①全纯凸性,即对于M中的任何紧子集K,集合
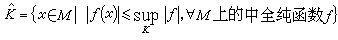 也是M中的紧子集;②它有足够多的全纯函数,即对于M中任何二个不同的点x1、x2都存在M上的全纯函数ƒ,使ƒ(x1)≠ƒ(x2);③对于任何x∈M,都存在M上的全纯函数ƒ1,ƒ2,…,ƒn,使ƒ1,ƒ2,…,ƒn可作为x附近的局部坐标。这时M称为施泰因流形。施泰因流形的函数论刻画是格劳尔特给出的,而其几何特征则是由E.毕晓普、R.纳拉西姆汉给出的:若复流形是施泰因流形则它可嵌入某一CN中成为后者的闭子复流形。
也是M中的紧子集;②它有足够多的全纯函数,即对于M中任何二个不同的点x1、x2都存在M上的全纯函数ƒ,使ƒ(x1)≠ƒ(x2);③对于任何x∈M,都存在M上的全纯函数ƒ1,ƒ2,…,ƒn,使ƒ1,ƒ2,…,ƒn可作为x附近的局部坐标。这时M称为施泰因流形。施泰因流形的函数论刻画是格劳尔特给出的,而其几何特征则是由E.毕晓普、R.纳拉西姆汉给出的:若复流形是施泰因流形则它可嵌入某一CN中成为后者的闭子复流形。几何上最简单而常见的复流形是被称为凯勒流形的一类。凯勒流形,简单地说,满足以下条件:对流形上的任何一点,可以选择这样的局部坐标z1,z2,…,zn,在此局部坐标下其度量
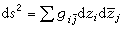 可表为,
可表为,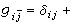
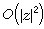 。换言之,凯勒流形上的度量如果和欧氏空间Cn的度量
。换言之,凯勒流形上的度量如果和欧氏空间Cn的度量 比较起来,两者的密合是二阶的。 对紧致凯勒流形的几何和拓扑性质人们已经进行了大量的研究。主题之一是,利用它的几何性质(由曲率表征)来获取其拓扑信息(由同调群表征)。这方面的基本结果,所谓消没定理,是小平邦彦得到的。例如,其中一个典型结果是,紧致凯勒流形M,如果其凯勒度量下的里奇曲率为正,则对任何正整数q,都有H(0,q)(M,C)=0,这里H(0,q)(M,C)是M上取值于(0,q)形式芽层的上同调群。
比较起来,两者的密合是二阶的。 对紧致凯勒流形的几何和拓扑性质人们已经进行了大量的研究。主题之一是,利用它的几何性质(由曲率表征)来获取其拓扑信息(由同调群表征)。这方面的基本结果,所谓消没定理,是小平邦彦得到的。例如,其中一个典型结果是,紧致凯勒流形M,如果其凯勒度量下的里奇曲率为正,则对任何正整数q,都有H(0,q)(M,C)=0,这里H(0,q)(M,C)是M上取值于(0,q)形式芽层的上同调群。在复流形的研究中,以流形的切空间为背景发展起来的复向量丛的概念是一个重要的概念。复流形M上的一个复向量丛,直观地说,就是M上每一点都“粘附”上一个有限维的复向量空间,这种“粘附”满足以下规则:对任何x∈M,以Kx表示在x点粘附的复向量空间(称为x上的纤维)。因为M是复流形,x可以有不同的局部坐标领域U和V,x∈U∩V。U 的局部坐标和V的局部坐标之间的关系是全纯的。Kx中同一向量的坐标在U和V下有不同的表示,这两个表示之间的关系由一个m×m矩阵(m=Kx的维数)给出,这个矩阵称为联接函数。如果联接函数对局部坐标来说是全纯的,并且其行列式在U∩V中恒不为零。这样所得到的M连同其各点的纤维组成的总空间E 称为M上的复向量丛。各点纤维Kx的维数称为此向量丛的秩。不难证明,复向量丛本身也是一个复流形。如果复向量丛的秩为1,这样的丛称为复线丛。
对于复流形M上的复向量丛K,可以考虑取值于K的无穷次可微的(p,q)微分形式。这种形式就局部来说可以写成
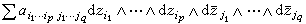 ,其中
,其中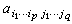 (x)是属于x的纤维Kx中的向量,并且当x变动时是x的无穷次可微函数。通过它,可以定义M上的取值于向量丛K的同调群H(p,q)(M,K)。
(x)是属于x的纤维Kx中的向量,并且当x变动时是x的无穷次可微函数。通过它,可以定义M上的取值于向量丛K的同调群H(p,q)(M,K)。对于紧致复流形上的复向量丛,基本的结果是霍奇定理,该定理断言:上同调群H(p,q)(M,K)是有限维的,并且其维数等于取值于K的(p,q)调和形式的线性无关数。这个定理由于将流形上的分析结构与拓扑结构联系起来,而成为复流形理论的基石之一。
关于紧复流形的另一重要结果是小平邦彦的嵌入定理。它断言,紧复流形如果具有一正的线丛,那么它就可以嵌入复射影空间而成为代数流形,即由有限个多项式零点所组成。
层及以层为系数的上同调群 层和以层为系数的上同调群的概念最早是法国数学家勒雷由于拓扑的需要而引进的,后由于韦伊、H.嘉当、J.P.塞尔等人的改进,成了近代多复分析及代数几何的基本工具。它是研究全纯函数的局部性质过渡到整体性质的有力方法。也是迄今为止处理比复流形更广的对象──复空间的最有效方法。所谓复空间就是其每点p的局部和 Cn(p)中某开集的一个解析集相同的集合。精确地说,一个豪斯多夫拓扑空间 M说是复空间,如果有M的一族开集覆盖{Uk},对每个k,存在
 中某开集Ωk的一个解析集Vk及一一连续映射
中某开集Ωk的一个解析集Vk及一一连续映射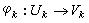 ,使得在
,使得在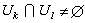 时,映射
时,映射 是全纯映射,即在 Vk的某个领域Ω
是全纯映射,即在 Vk的某个领域Ω 中存在全纯映射
中存在全纯映射 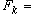
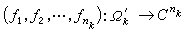 ,使
,使 是Fk对Vk的限制。
是Fk对Vk的限制。如果将施泰因流形的定义中复流形M改成复空间M,那就可以照搬过来得到施泰因空间的概念。设M是一个复空间,任取一点x∈M。两个在x局部全纯的函数如果在x的一个更小的邻域上恒同的话,则称两者属于同一个全纯函数的芽。因此,任一定义于M的某开集的全纯函数在它的定义域的每一点都惟一确定了一个芽。将M上所有这些局部全纯函数的芽合在一起,赋以适当的拓扑,所组成的拓扑空间就称为M上全纯函数的芽层。同样,可以仿此定义M上光滑函数、连续函数、常数函数等的芽层。若M是复流形,则还可定义(p,q)微分形式等的芽层。概而言之,M上某类函数的芽层在一点的芽就是由所有在该点的局部有定义的该类函数所组成。设U是M的一个开集,F是M上某类函数的芽层。在U的每一点取F在该点的一个芽,所有这些如果可以连续地接成一片,就称为U上层F的一个截面。事实上,层F在U上的一个截面就是一个在U上定义的该类函数。以层为系数的上同调群就是通过截面来定义的。
任取复空间M的一个开集覆盖 u={Ui},令
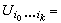
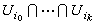 ,仍是M的一个开集。现设 F是M上的一个层,对每一个
,仍是M的一个开集。现设 F是M上的一个层,对每一个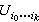 ,取层F的一个截面
,取层F的一个截面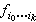 ,使其对下标反称。这样得到的ƒ=(
,使其对下标反称。这样得到的ƒ=(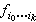 )称为一个k维上链。所有k维上链组成一个线性空间。在k-1维上链和k维上链之间可以自然地定义一个映射δ:ƒ→δƒ,
)称为一个k维上链。所有k维上链组成一个线性空间。在k-1维上链和k维上链之间可以自然地定义一个映射δ:ƒ→δƒ,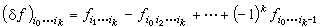 映射δ的显著性质是δ2=0。把满足δƒ=0的k维上链称为k维上闭链,而把形如ƒ=δg(g是某一k-1维上链)的k维上链称为k维上边缘链。那么由于δ2=0,上边缘链是上闭链的一部分。两者相差的程度可以用上闭链空间与上边缘链空间的商空间来刻画,这就是层F的上同调群,记作Hk(u,F),即:
映射δ的显著性质是δ2=0。把满足δƒ=0的k维上链称为k维上闭链,而把形如ƒ=δg(g是某一k-1维上链)的k维上链称为k维上边缘链。那么由于δ2=0,上边缘链是上闭链的一部分。两者相差的程度可以用上闭链空间与上边缘链空间的商空间来刻画,这就是层F的上同调群,记作Hk(u,F),即: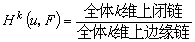 。应该指出,这样定义的上同调群Hk(u,F)依赖于开覆盖u。但是通过一定的极限手续或对覆盖中的开集加以适当的规格化,可以使所得上同调群仅与M有关而与具体的开覆盖 u无关,这样得到的上同调群就可以合理地称作M上以层F为系数的上同调群Hk(M,F)。
。应该指出,这样定义的上同调群Hk(u,F)依赖于开覆盖u。但是通过一定的极限手续或对覆盖中的开集加以适当的规格化,可以使所得上同调群仅与M有关而与具体的开覆盖 u无关,这样得到的上同调群就可以合理地称作M上以层F为系数的上同调群Hk(M,F)。大体说来,Hk(M,F)是将层F的局部截面“拼接”成整体截面的可能性的一种度量。
以层论为基础,结合H.嘉当、岡潔等关于全纯函数理想论的研究,发展成为疑聚解析层的概念。利用疑聚解析层的理论,H.嘉当、塞尔将全纯域的基本理论系统地推广到施泰因空间上,而得到施泰因空间的基本定理──嘉当定理A与B。前者说,施泰因空间上的任何凝聚解析层在每一点都可由有限个整体截面生成。后者说,对于施泰因空间M上的任何凝聚解析层F,上同调Hk(M,F)=0,凬k≥1。事实上,嘉当定理 B还可用来定义施泰因空间,即若对复空间M上的任何凝聚解析层F,上同调Hk(M,F)=0,凬k≥1,那么M称为施泰因空间。
黎曼-罗赫定理及其推广 黎曼-罗赫定理是黎曼曲面理论的基本定理。概括地说,它是研究在闭黎曼曲面上有多少线性无关的亚纯函数 (在给定的零点和极点上,其重数满足一定条件)?所谓闭黎曼曲面,就是紧致的一维复流形。拓扑上,它相当于球面上连接了若干个柄。柄的个数g是曲面的拓扑不变量,称为亏格。在闭黎曼面M上取定有限个点αi, 对每一αi附以非零整数ni(ni>0表示ni重零点,ni<0表示|ni|重极点),作形式和D=∑niαi称为除子,d(D)=∑ni称为除子D的阶数。每个亚纯函数ƒ自然具有惟一的除子,记以(ƒ),不仅如此,每一亚纯微分ω(亚纯微分是M上局部可以表为φ(z)dz的微分式,其中z是局部坐标,φ(z)是z 的亚纯函数)也有惟一确定的除子(ω)。利用这一概念,黎曼-罗赫定理可表述为:对于任意给定的除子D,M上存在多少个线性无关的亚纯函数ƒ,使ƒ的除子(ƒ)满足(ƒ)+D≥0?这一线性无关数如果记作l(D),同时记i(D)为M上线性无关的亚纯微分ω 的个数,它们满足(ω)-D ≤0,那么,著名的黎曼-罗赫定理(1865)可以表为:l(D)-i(D)=d(D)-g+1。例如,取D=0,因而d(D)=0,此时黎曼-罗赫定理给出:M上线性无关的全纯微分的个数等于其亏格数。
鉴于黎曼-罗赫定理将复结构与拓扑结构沟通起来的深刻性,如何推广这一定理到高维的紧复流形自然成为数学家们长期追求的目标。模仿式的推广是行不通的,例如高维情况下“除子”如何定义就是问题。解决的办法只能是对黎曼-罗赫定理给以新的说法,使在新说法中出现的各个量可以推广到高维复流形上去。而这一切只是在层及上同调概念引进并应用于复分析以后才有可能。途径是这样的:对M上任何给定的除子D,可以联系一个复线丛λ(D)。这一线丛又决定了它的全纯截面的芽层。于是,l(D)等于取值于λ(D)的全纯截面芽层的0维同调群的维数dimH0(M,λ(D)),i(D)等于dimH1(M,λ(D),d(D)等于线丛λ(D)的陈数(一种表征拓扑性质的示性数)X(λ(D)),而2(1-g)等于M本身的陈数с(M)。这样,黎曼-罗赫定理就可以改述成:
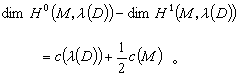
塞尔首先注意到这样的改述。对一般的紧复流形M,设K是M上的复向量丛,以Hq(M,E)表M上取值于K的全纯截面芽层的q维上同调群,令
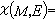
 。塞尔提出(1953),能否将ⅹ(M,K)用M的陈类及复向丛K的陈类的多项式加以表达?第二年,F.希策布鲁赫成功地作到了这一点。他所得到的公式即称为希策布鲁赫-黎曼-罗赫公式。以M上的全纯线丛L为例,所得的公式为
。塞尔提出(1953),能否将ⅹ(M,K)用M的陈类及复向丛K的陈类的多项式加以表达?第二年,F.希策布鲁赫成功地作到了这一点。他所得到的公式即称为希策布鲁赫-黎曼-罗赫公式。以M上的全纯线丛L为例,所得的公式为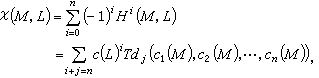 式中Tdj是一些与M无关的普适的多项式,称为托德多项式。
式中Tdj是一些与M无关的普适的多项式,称为托德多项式。希策布鲁赫-黎曼-罗赫公式曾引起了一系列新的研究和推广。到目前为止,最重要的推广是阿蒂亚-辛格的指数定理(1962)。M.F.阿蒂亚、I.M.辛格从紧黎曼流形上向量丛间椭圆微分算子的“指数”的角度,得到了更一般的公式,它是以希策布鲁赫-黎曼-罗赫公式为其特例。不仅如此,它还同时统一了其他几个著名的经典定理,因而被誉为近代数学的重大成就之一。
齐性域与对称域 Cn中的有界连通开集称为有界域。单复变的黎曼映射定理说,C 中边界多于一点的单连通域都全纯等价于单位圆|z|<1。多复变的相应问题要远为复杂,至今离问题的解决还很远。目前,多复变中对一般有界域的全纯分类几乎没有什么结果。研究集中在性质较好的一类:有界齐性域。
设Ω为Cn中的有界域。Ω到自身的双方一一的全纯映射称为Ω的解析自同构。全体解析自同构在映射的乘法下组成一个群,记作Aut(Ω)。关于Aut(Ω)的结构,第一个基本的结果属于H.嘉当(1935):Aut(Ω)的包含单位元的连通分支是一个实李群。如果Ω中任何两点,都存在一个解析自同构将其中一点变成另一点,则Ω称为齐性的。因为单位圆是齐性的,再加上黎曼映射定理,所以C中任何有界单连通域都是齐性域。多复变中情况就没有这么简单。设Ω是有界齐性域。任意固定其中一点,Aut(Ω)中保持该点不动的解析自同构组成Aut(Ω)的一个子群,记作K。于是,Ω=Aut(Ω)/K。这样,就将有界齐性域和李群对其闭子群的商空间联系了起来。有界齐性域的研究因而化归李群的研究。研究李群的代数工具是李代数。李代数就其实质来说,是李群的单参数子群的无穷小生成元。同时,因为Aut(Ω)/K具有齐性的复结构,这就对有界齐性域的李代数赋予了特殊的限制。由此出发,皮亚捷茨基-沙皮罗证明了:任何有界齐性域均解析等价于他所定义的西格尔域。鉴于西格尔域的实现相当明确,这一结果无疑是有界齐性域分类问题的重要进展。
在有界齐性域中研究得最为深入的是对称域。所谓“对称”是由单位圆的下述性质抽象出来的:对于|z|<1,存在解析自同构 g:z→-z。这一映射只以O为不动点,且将通过Ο的所有测地线都反转了过来。有界齐性域Ω,如果对任意的z∈Ω,都存在g∈Aut(Ω),满足:①g(z)=z,且z是g的惟一不动点;②g2=1,则Ω称为对称域。显然,对称域是有界齐性域中与单位圆更相近似者。将对称域在解析等价意义下加以分类,是É.嘉当的重大贡献(1936)。他利用他首创的黎曼对称空间的理论,给出了对称域分类的完整结果:任何对称域都是一些既约对称域的拓扑积。而既约对称域共四大类,外加两个例外域(其复维数分别是16和27)。前四大类对称域中国数学家华罗庚称之为典型域。如果用矩阵实现,它们是:
 。
。 。
。 。
。
 对这四类典型域,华罗庚和陆启铿进行了系统的研究。他们解决了与典型域调和分析及几何有关的许多基本问题:解析自同构群、柯西积分公式、核函数、完整正交系、调和函数论、施瓦兹常数等。
对这四类典型域,华罗庚和陆启铿进行了系统的研究。他们解决了与典型域调和分析及几何有关的许多基本问题:解析自同构群、柯西积分公式、核函数、完整正交系、调和函数论、施瓦兹常数等。多复变的自守函数 设Ω是Cn中的有界域。Ω的全体解析自同构组成群Aut(Ω)。Aut(Ω)的子群Γ称为不连续的,如果对于Ω中的任何点x,都存在一个领域U,使得Γ中仅有有限个元素σ,使σ(U )和U 相交。所谓自守函数就是相对于某个不连续子群Γ而言的。相对Γ的自守函数,指的是定义于Ω的亚纯函数,它在Γ下不变,即对任何x∈Ω和任何γ∈Γ,ƒ(γ(x))=ƒ(x)。在自守函数的研究中,一个主要的概念是基本域。如果Γ是一个不连续子群,那么Ω在 Γ的作用下分成一个个互不相交的“轨道”Γx。以这些轨道为元素组成的空间Ω/Γ称为Γ的基本域。基本域具有自然的拓扑结构,一般是一复空间。自守函数因为在Γ下不变,它自然可以看成基本域上的亚纯函数。早在19世纪末,庞加莱就提出了一套如何构造自守函数的有效方法。他用无穷级数首先构造自守形式,再由自守形式的商求得自守函数。这种级数后人称之为庞加莱级数。所得自守形式,是定义于Ω上的全纯函数ƒ,满足对任何σ∈Γ,有ƒ(σ(z))=jσ(z)·ƒ(z)。这里jσ(z)称为自守因子,是Ω上的亚纯函数,其特征性质为:对于任何σ,τ∈Γ有:
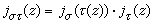 。显然,对应于同一自守因子的两自守形式之商自然是一个自守函数。自守函数论中最常用的自守因子是以下形式:
。显然,对应于同一自守因子的两自守形式之商自然是一个自守函数。自守函数论中最常用的自守因子是以下形式: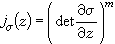 ,其中
,其中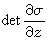 是映射σ的函数行列式。自守函数论的中心问题是研究自守函数组成的域的代数结构。20世纪中叶以前,这方面的主要贡献属于西格尔。在基本域紧致的情况下,西格尔证明了:任一自守函数都可以写成自守形式之商;任意n+1个自守函数都是代数相关的;可以选择n+1个自守函数ƒ0,ƒ1,…,ƒn,使任何自守函数都能表成它们的有理函数。此外,西格尔依据他对二次型的解析理论的出色研究,构造了一大批具有重要意义的基本域的例子(紧致的和非紧致的)。这些例子都与代数群的算术子群密切相关。50年代以后,自守函数研究的重点转向基本域非紧但体积有限的情况。这方面,随着赛尔伯格“求迹公式”的提出,盖尔范德、朗兰兹等人揭示了自守函数与李群的无穷维表示、代数数论等的内在联系,引起了大量的深入研究。时至今日,这一领域正处于近代数学的众多分支:复分析、代数几何、代数群、代数数论、李群等的交汇点,其重要性正与日俱增。
是映射σ的函数行列式。自守函数论的中心问题是研究自守函数组成的域的代数结构。20世纪中叶以前,这方面的主要贡献属于西格尔。在基本域紧致的情况下,西格尔证明了:任一自守函数都可以写成自守形式之商;任意n+1个自守函数都是代数相关的;可以选择n+1个自守函数ƒ0,ƒ1,…,ƒn,使任何自守函数都能表成它们的有理函数。此外,西格尔依据他对二次型的解析理论的出色研究,构造了一大批具有重要意义的基本域的例子(紧致的和非紧致的)。这些例子都与代数群的算术子群密切相关。50年代以后,自守函数研究的重点转向基本域非紧但体积有限的情况。这方面,随着赛尔伯格“求迹公式”的提出,盖尔范德、朗兰兹等人揭示了自守函数与李群的无穷维表示、代数数论等的内在联系,引起了大量的深入研究。时至今日,这一领域正处于近代数学的众多分支:复分析、代数几何、代数群、代数数论、李群等的交汇点,其重要性正与日俱增。