多相流体力学(卷名:力学)
fluid dynamics of multiphase systems
研究同种或异种化学成分物质的固-气、液、-气、液-液或固-液-气系统共同流动规律的学科。“相”(phase)可以指不同的热力学集态(固、液、气等),也可以指同一集态下不同的物理性质或力学状态(同一地点不同尺寸和速度或不同材料密度的颗粒或气泡等)。多相流动广泛存在于自然界和工程设备中,如含尘埃的大气和云雾、含沙水流、各种喷雾冷却、粉末喷涂、血管流、含固体粉末的火箭尾气、炮膛内火药颗粒及其燃烧产物的流动等。就大量工程问题而言,多相流体力学主要应用于粉粒物料的管道输送、颗粒分离和除尘、液雾和煤粉悬浮体燃烧及气化、流化床和流化床燃烧以及锅炉、反应堆、化工、冶炼及采油等装置中气-液流动等方面,其目的是节省管道输送能量,提高分离或除尘效率,改善传热传质或燃烧中颗粒混合,改善锅炉中水循环,提高反应堆冷却的安全性等。多相流体力学的研究对象是探讨流场中各个相的速度、压力、温度、组分浓度、体积分数、相和相之间的相互作用以及各相与壁面间相互作用,以便弄清其中的动量传递、传热、传质、化学反应,甚至电磁效应的规律。
研究内容 多相流体力学主要分成气-固多相(或两相)流和气-液两相流两个较大的分支。多相流体力学研究的根本出发点是建立多相流模型和基本方程组。在此基础上分析各相的压力、速度、温度、表观密度和体积分数、气泡或颗粒尺寸分布、相间相互作用(如气泡或颗粒的阻力与传热传质)、颗粒湍流扩散、流型、压力降、截面含气率、流动稳定性、流动的临界态等。
多相流体力学的模型和基本方程组 描述多相流体可用不同的模型。对各相尺寸均较大(与流动的几何尺寸相比)的体系,可对各相内部分别运用单向流体力学的模型写出其各自的基本方程组。若分散相的尺寸不太大,一般用体积平均概念,即认为各项占据同一空间并且相互渗透。这种情况下可采取统一的连续介质模型来描述多相流,其中又可以分成无相间滑移的单流体模型(这时不同的相只看成是流体的不同组合)和有滑移的多流体模型或双流体模型。按后一模型,空间各点处每个相可有其各自不同的速度、体积分数、温度。对颗粒群悬浮体多相流,除上述模型外还有非连续介质的分散群的轨道模型和统计群模型。按照有滑移的流体模型,常见的无化学反应、相间有传热传质的湍流多相流基本方程组为:
k相连续性方程:
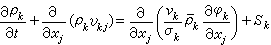 ;
;k相动量方程:
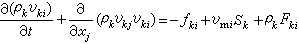

 ;
;k相能量方程(马赫数不大时):
 式中下标k表示k相;下标m表示多相混合物;下标i表示i方向分量;下标j表示坐标顺序;ρ、v、嗞、孒、p分别为表观密度、体积和时间平均速度、体积分数、材料密度和分压;fk为单位体积中其他各相对k相的阻力;Fk为k相单位质量所受的体力;νk为k相湍流粘性系数;σk为k相的湍流施密特数;Tk为k相温度;cpk为k相定压比热;Sk为k相与其他相质量交换所造成的物质源或汇,即单位时间单位体积内产生或消失的k相物质;λk为k相湍流热导率;Qk、Q
式中下标k表示k相;下标m表示多相混合物;下标i表示i方向分量;下标j表示坐标顺序;ρ、v、嗞、孒、p分别为表观密度、体积和时间平均速度、体积分数、材料密度和分压;fk为单位体积中其他各相对k相的阻力;Fk为k相单位质量所受的体力;νk为k相湍流粘性系数;σk为k相的湍流施密特数;Tk为k相温度;cpk为k相定压比热;Sk为k相与其他相质量交换所造成的物质源或汇,即单位时间单位体积内产生或消失的k相物质;λk为k相湍流热导率;Qk、Q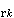 分别为k相与其他相以及环境间的对流换热和辐射换热。
分别为k相与其他相以及环境间的对流换热和辐射换热。表观密度和体积分数 多相流单位体积中所含某一相的质量称为该相的表观密度。表观密度ρk和真实的材料密度孒k间的关系为ρk=嗞k孒k,嗞k为k相体积分数;多相混合物的表观密度为
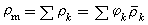 。 对于颗粒群悬浮体多相流,其表观密度为ρk=nkmk,多相混合物的表观密度为
。 对于颗粒群悬浮体多相流,其表观密度为ρk=nkmk,多相混合物的表观密度为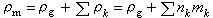 ,式中ρg为气相表观密度;nk为多相流单位体积中k种颗粒数;mk为每个k种颗粒的质量,mk=孒kπd婮/6,dk为k种颗粒直径。颗粒群体积分数为
,式中ρg为气相表观密度;nk为多相流单位体积中k种颗粒数;mk为每个k种颗粒的质量,mk=孒kπd婮/6,dk为k种颗粒直径。颗粒群体积分数为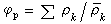 。嗞p较小时,例如平均小于0.02%的液雾或煤粉火焰,称为稀疏颗粒群。嗞p较大时,例如 嗞p≈0.8的流化床或炮膛中流动的火药粒,可称为稠密颗粒群。
。嗞p较小时,例如平均小于0.02%的液雾或煤粉火焰,称为稀疏颗粒群。嗞p较大时,例如 嗞p≈0.8的流化床或炮膛中流动的火药粒,可称为稠密颗粒群。多相流颗粒群尺寸分布 尺寸不均匀的颗粒群通常服从罗辛-拉姆勒分布律,即R=exp[-(d/廀)n)],式中d为颗粒群中任一种的尺寸;R为大于该尺寸的部分所占相对重量百分数;廀和n为经验常数,分别反映细度和不均匀度。颗粒平均直径可按直径、面积或体积取平均。常用的为索特平均直径,其定义为
 ,式中npk、dk分别为k种尺寸组的数目密度及其直径。
,式中npk、dk分别为k种尺寸组的数目密度及其直径。多相流颗粒阻力和传热传质 颗粒与流体间有相对运动时的阻力为:
Fc=AρfCd|vp-vf|(vp-vf)/2,式中A为颗粒迎风截面积;ρf为流体密度;vp和vf分别为颗粒和流体速度;Cd为阻力系数,Cd的半经验公式为:
Cd=(2+A Repm)12/Rep,式中Rep=|vp-vf|d/νf,d为颗粒直径,νf为流体运动粘度;A和m为常数,取决于不同的Rep。Rep《1时取A=0,上式为斯托克斯阻力公式。Rep<1时取A=3/8和m=1,上式为奥岑公式。Rep<1000时取A=0.3和m=0.687,为沃利斯公式等。无相变时颗粒与流体间传热传质可用兰兹-马歇耳公式表达,即
 式中Nu=hd/λ为努塞尔特数,h为对流传热系数,λ为分子热导率;
式中Nu=hd/λ为努塞尔特数,h为对流传热系数,λ为分子热导率; =hdd/Dm为舍伍德数,hd为对流传质系数,Dm为分子扩散系数;Pr=μcp/λ为普朗特数,μ为动力粘性系数,cp为流体定压比热;
=hdd/Dm为舍伍德数,hd为对流传质系数,Dm为分子扩散系数;Pr=μcp/λ为普朗特数,μ为动力粘性系数,cp为流体定压比热; =ν/Dm为施密特数,ν为运动粘性系数。有蒸发或升华的颗粒,其传热律为:
=ν/Dm为施密特数,ν为运动粘性系数。有蒸发或升华的颗粒,其传热律为:Nue=Nu ln(1+B)/B,式中B=
 (Tf-Tp)/qe,其中Tf为流体温度;Tp为颗粒温度;qe为蒸发热或升华热。
(Tf-Tp)/qe,其中Tf为流体温度;Tp为颗粒温度;qe为蒸发热或升华热。多相流颗粒湍流扩散 颗粒在流体中除了因时平均运动产生的轨道效应外,还有因流体湍流脉动而造成的湍流扩散(见扩散)。流体的湍流粘性越高,颗粒越小,则颗粒湍流扩散系数越大,并且越接近于流体的湍流扩散系数。反之,流体湍流粘性越低,颗粒越大,则颗粒湍流扩散也越小。为了改善混合,常常要强化湍流扩散。
气液两相流的流型(或流态) 气液两相在管道中流动时因压力、流量、热负荷、流动方向、管道几何特性、工质物性等的不同,能形成各种不同的流型。竖管中最常见的流型(见图)有:细小气泡散布于液相中的气泡状流型;管中心为气弹及壁附近为连续液膜的气弹状流型;管中心为夹带细小液滴的气核和壁附近为连续液膜的环状流型;气相中含细小液滴和壁附近无连续液膜的雾状流型。不同的流型有不同的流体动力学和传热传质规律。
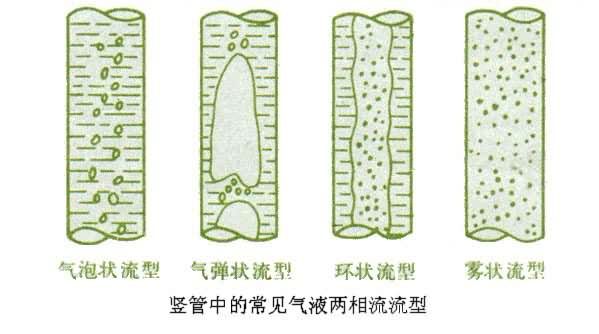
气液两相流动压力降 两相流通过管道时引起的压差称为压力降。气液两相流压力降有四种:由于气液两相摩擦引起的摩擦压力降;由于克服重位差引起的重位压力降;由于两相流体加速引起的加速压力降和由于克服管路中各种局部阻力引起的局部阻力压力降。
摩擦压力降可按巴罗奇关系式计算,即
Δpf=2foG2L╃
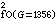 Ω/ρ1D,式中fo为液相摩擦阻力系数;G为质量流速;L为计算管段长度;D为管道内径; ╃
Ω/ρ1D,式中fo为液相摩擦阻力系数;G为质量流速;L为计算管段长度;D为管道内径; ╃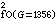 为G=1356千克/(米2·秒)时的两相折算系数,可按管道中重量含气率χ,气相和液相粘性系数μg、μ1,气相和液相密度ρg、ρ1在后面所列参考书目中查得;Ω 为G不等于1356千克/(米2·秒)时对╃娳影响的修正系数,也和G、μg、μ1、ρg、ρ1有关。
为G=1356千克/(米2·秒)时的两相折算系数,可按管道中重量含气率χ,气相和液相粘性系数μg、μ1,气相和液相密度ρg、ρ1在后面所列参考书目中查得;Ω 为G不等于1356千克/(米2·秒)时对╃娳影响的修正系数,也和G、μg、μ1、ρg、ρ1有关。重位压力降可按下式计算:
ΔpG=[αρg+(1-α)ρ1]gLsinθ,式中α为管段平均截面含气率;g为重力加速度;L为含气段长度;θ为管段和水平方向间倾角。
加速压力降可按下式计算:
 式中χi及χe分别为管段进口及出口处重量含气率;ai和αe分别为管段进口及出口处截面含气率。
式中χi及χe分别为管段进口及出口处重量含气率;ai和αe分别为管段进口及出口处截面含气率。突扩管道引起的局部阻力压力降可按罗米关系式计算,即
 式中A1及A2分别为小管道及大管道截面积。
式中A1及A2分别为小管道及大管道截面积。设计有两相流动的设备时,必须计算两相流的压力降以便确定所需动力,保证设备安全经济地运转。
气液两相流截面含气率 气液两相任意流通截面中气相截面所占总流通截面积的份额称为截面含气率。它是计算重位压力降和加速压力降等的必不可少的参量。可用适合于各种介质的休马克关系式表示为:
α=Kβ,式中α为截面含气率;β为容积含气率;K为比例系数,
K=f(z),而
z={DG/[(1-α)μ1+αμg]}戃[W 2/(gD)]勂(1-β)戂,式中W为双相混合物流速。当z<10时,
K=-0.16376+0.31037z-0.03525z2
+0.001366z3。当z>10时,
K=0.75545+0.003585z-0.1436×10-4z2。
气液两相流动稳定性 气液两相流受湍流干扰或其他干扰,其流动参量总是随时间略有变化,凡其时平均运动不随时间变化的可称为稳定流动,反之则称为不稳定流动。两相流动中有时会出现不稳定现象,持续的不稳定两相流常常使部件振动,影响传热,并引起金属疲劳而使设备提前损坏。流动不稳定性的机理目前还不大清楚,根据经验可以找出其预测及防范措施。
气液两相临界流动 气液两相流从一容器通过管道排出时,对应于容器内的压力和重量含气率有一个可能的最大流量,称为临界流量。发生临界流量的工况称为临界流动。短管中双组分气流两相临界流量Gc可按下列均质流模型的公式计算:
Gc=[χ(vgc/ag)2+(1-χ)(v1c/a1)2]戂,式中χ 为重量含气率;vgc和v1c分别为气相和液相比容;ag和a1分别为气相和液相的声速。
临界流动问题对研究管道最大排放量是重要的。
研究方法 主要有半经验物理模型和统观实验法,数学模型及数值计算法,局部场的实验量测法等。
半经验物理模型和统观实验法 半经验物理模型指以实验观测为基础对多相流的流动形态作出半经验性的简化假设以便进行简化分析计算,如假定多相流为一维柱塞流 (plug flow)等。统观实验法指只研究外部参量变化规律,例如多相流在管道中的阻力或平均传热量与流速间的关系、平均的体积分数等,不研究多相流中各种变量的场分布规律。
数学模型和数值计算法 对多相流基本方程组中各个湍流输运项、相间相互作用项和源项的物理规律以实验或公设为基础提出一定的表达式,使联立的方程组封闭,能够求解,这就是建立数学模型。联立的非线性偏微分方程组只能用数值法,如有限差分方法或有限元法求解。已经制定了二维和三维多相湍流流动计算程序软件,可以初步用于计算旋风除尘器、煤粉燃烧室和气化室、液雾燃烧室、反应堆中水-汽系统以及炮膛中气-固或气- 液各相中的压力、速度、温度、体积分数等的分布。目前,正在研制用于工程中最优化设计的软件。
实验量测法 研究多相流的流动、传热、传质以及化学反应等规律时,观测其流型,测量各相的速度、流量、尺寸、浓度、体积分数或含气率、温度分布等十分重要。观测流型常常用高速摄影、全息照相和电测法等。测量颗粒尺寸分布可用印痕或溶液捕获法、光学或激光散射法、激光全息术、激光多普勒法 (LDV法)等。测量流量、速度、浓度、重量含气率分布等可以用 LDV法、取样探针、电探针、光导纤维探针、分离器法等。测量平均截面含气率可用放射性同位素法、γ射线法、分离器法等。
参考书目
S.L.Soo, Fluid Dynamics of Multiphase Systems,Blaisdell Pub. Waltham, Massachusetts,1967.
G. F. Hewitt,Measurement of Two-phase Flow Parameters,Academic Press, London, 1978.
G.Hetsroni,ed., Handbook of Multiphase Systems,Hemisphere Pub.Corp.,Washington,1982.
D. B. Spalding , Numerical Computations of Multiphase Flows,Imp.Coll.Sci.Tech. HTS/81/8,London,1981.