多项式(卷名：数学)
polynomial
代数学中最基本的研究对象之一。设αi（i=0，1，…，n）是域F中元素，x是一个文字（或称符号），则形如
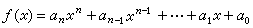的表示式，称为F上的一个文字x的多项式，简称为一元多项式。αn，αn-1，…，α1，α0称为ƒ(x)的系数，αkxk称为k次项，αk称为k次项系数。如果αn≠0，那么ƒ（x）称为n次多项式，此时αnxn称为ƒ(x)的首项，αn称为ƒ(x)的首项系数。两个多项式相等是指它们的同次项的系数都相等。系数全为零的多项式，称为零多项式，记作0，并约定零多项式的次数为－
。F上的两个多项式
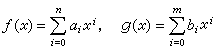之和定义为
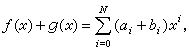(1)式中N=max{n，m}，并约定当t>n时，αt=0；对 g(x)的系数也有同样的规定。ƒ(x)+g(x)仍是 F 上一个多项式。ƒ(x)与g(x)的积定义为
(2)式中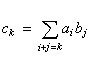
。用F[x]表示系数在域F中的多项式全体，用公式(1)、(2)定义F[x]的加法以及乘法，则F[x]成一个环，称之为F上的一元多项式环。F[x]是具有单位元素的整环。
设ƒ(x)和g(x)是F[x]中的两个多项式，若存在F[x]中一个多项式q(x)，使得ƒ(x)=q(x)g(x)，则称ƒ(x)是g(x)的一个倍式，g(x)是ƒ(x)的一个因式。应用带余除法可以判断g(x)是否是ƒ(x)的一个因式。
带余除法 若 ƒ(x)和g(x)是F[x]中的两个多项式，且 g(x)≠0，则在F[x]中有多项式 q(x)和r(x)，满足ƒ(x)=q(x)g(x)+r(x)，其中r(x)的次数小于g(x)的次数，且只有一对q(x)和r(x)满足这些条件。此时q(x) 称为g(x)除ƒ(x)的商式，r(x)称为余式。当g(x)=x-α时，则r(x)=ƒ(α)称为余元，式中的α是F的元素。此时带余除法具有形式ƒ(x)=q(x)(x-α)+ƒ(α)，称为余元定理。g(x)是ƒ(x)的因式的充分必要条件是g(x)除ƒ(x)所得余式等于零。如果g(x)是ƒ(x)的因式，那么也称g(x) 能整除ƒ(x)，或ƒ(x)能被g(x)整除。特别地，x-α是ƒ(x)的因式的充分必要条件是ƒ(α)=0，这时称α是ƒ(x)的一个根。
如果d(x)既是ƒ(x)的因式，又是g(x)的因式，那么称d(x)是ƒ(x)与g(x)的一个公因式。如果d(x)是ƒ(x)与g(x)的一个公因式，并且ƒ(x)与g(x)的任一个因式都是d(x)的因式，那么称d(x)是ƒ(x)与g(x)的一个最大公因式。如果ƒ(x)=0，那么g(x)就是ƒ(x)与g(x)的一个最大公因式。当ƒ(x)与g(x)全不为零时，可以应用辗转相除法来求它们的最大公因式。
辗转相除法 已知 F[x] 中两个不等于零的多项式ƒ(x)与g(x)，用g(x)除ƒ(x)得商式q1(x)、余式r1(x)。若r1(x)=0，则g(x)就是ƒ(x)与g(x)的一个最大公因式。若 r1(x)≠0，则用 r1(x)除 g(x)得商式q2(x)、余式r2(x)。若r2(x)=0，则r1就是ƒ(x)与g(x)的一个最大公因式。否则，如此辗转相除下去，余式的次数不断降低，经有限s次之后，必有余式为零，即有如下的一组等式：
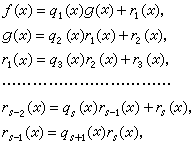式中r1(x)、r2(x)、…、rs(x)都不为0，于是rs(x)就是ƒ(x)与g(x)的一个最大公因式。利用辗转相除法的算法，可将ƒ(x)与g(x)的最大公因式rs(x)表成ƒ(x)和g(x)的组合，而组合的系数是F上的多项式。
如果ƒ(x)与g(x)的最大公因式是零次多项式，那么称ƒ(x)与g(x)是互素的。最大公因式和互素概念都可以推广到几个多项式的情形。
如果F[x]中的一个次数不小于1的多项式ƒ(x)，不能表成 F[x] 中的两个次数较低的多项式的乘积，那么称ƒ(x)是F上的一个不可约多项式。
任一多项式都可分解为不可约多项式的乘积。
惟一分解定理 F[x]中任一个次数不小于 1的多项式都可以分解为F上的不可约多项式的乘积，而且除去因式的次序以及常数因子外，分解的方法是惟一的。
当F是复数域C时，根据代数基本定理，可证C[x]中不可约多项式都是一次的。因此，每个复系数多项式都可分解成一次因式的连乘积。
当F是实数域R时，由于实系数多项式的虚根是成对出现的，即虚根的共轭数仍是根，因此R[x]中不可约多项式是一次的或二次的。所以每个实系数多项式都可以分解成一些一次和二次的不可约多项式的乘积。实系数二次多项式αx2+bx+с不可约的充分必要条件是其判别式b2-4αс<0。
当F是有理数域Q时，情况复杂得多。要判断一个有理系数多项式是否不可约，就较困难。应用本原多项式理论，可把有理系数多项式的分解问题化为整系数多项式的分解问题。一个整系数多项式如其系数是互素的，则称之为本原多项式。每个有理系数多项式都可表成一个有理数及一个本原多项式的乘积。关于本原多项式有下述重要性质。
高斯引理：两个本原多项式的乘积是本原多项式。
应用高斯引理可证，如果一个整系数多项式可以分解为两个次数较低的有理系数多项式的乘积，那么它一定可以分解为两个整系数多项式的乘积。这个结论可用来判断有理系数多项式的不可约性。关于Q[x]中多项式的不可约性的判断，还有艾森斯坦判别法：对于整系数多项式
，如果有一个素数p能整除αn-1，αn-2，…，α1，α0，但不能整除αn，且p2不能整除常数项α0，那么ƒ(x)在Q上是不可约的。由此可知，对于任一自然数n，在有理数域上xn-2是不可约的。因而，对任一自然数n，都有n次不可约的有理系数多项式。多项式方程 多项式理论的发展与多项式方程（代数方程）的研究有密切联系。一个未知量的高次方程的一般形式为
(3)令
于是方程(3)的根即多项式ƒ(x)的根。在20世纪以前，解方程一直是代数学的一个中心问题。远在公元以前，文明古国的学者对于某些特殊二次方程的解法，已经有所研究。在16世纪才得到三次方程和四次方程的解法。
二次方程αx2+bx+с=0的求根公式为
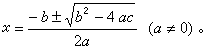(4)求解三次方程
(5)先利用变换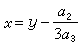
将(5)化为
(6)再作变换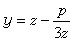 
，将（6）化为关于 z3的二次方程
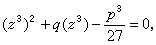应用公式(4)求出z3，即可得出方程(6)的三个根为
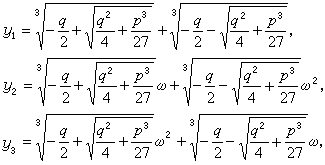式中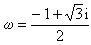
。因此方程（5）的根为
，
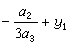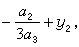
。求解四次方程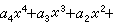
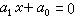，把它的根减去
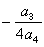而化为
(7)再令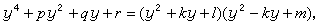
比较两端各项的系数，得
(8)如果q=0，那么方程(7)即为 y4+Py2+r=0，很容易求解。如果q≠0，那么k≠0，可由(8)中前两式解得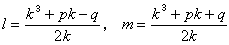
(9)代入(8)中第三式，即得
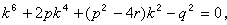解之，设k0是此方程的任一根，将其代入(9)得到l和 m的值l0和m 0，于是方程(7)化为
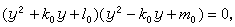由此可得方程(7)的4个根，再把各根加上
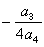就得出原方程的四个根。一个代数方程的解，如果可以由这个方程的系数经过有限次加减乘除以及开整数次方等运算表示出来，就称为这个方程的根式解。一、二、三、四次代数方程都有根式解，而五次和五次以上的代数方程就没有根式解（见伽罗瓦理论）。
根据多项式的根与一次因式的关系以及关于复系数和实系数多项式的因式分解定理，有以下结论：
每个复系数n次方程恰有n个复根(重根按重数计算)。
如果虚数α是实系数方程ƒ(x)＝0的一个根，那么ā（α的共轭数）也是这个方程的根，并且它们的重数也是相同的。
有理系数高次方程的求解，可归结为整系数方程的求解问题。如果有理数r/s是整系数方程(3)的一个有理根，其中r和s是互素的整数，那么r一定是α0的因数， s一定是αn的因数。特别地，若ƒ(x)的首项系数为1，则它的有理根都是整根，而且是常数项的因数。
插值多项式 在实际问题中，往往通过实验或观测得出表示某种规律的数量关系y＝F(x)，通常只给出了F(x)在某些点xi上的函数值yi=F(xi)，j=1，2，…，n+1。即使有时给出了函数F(x)的解析表达式，倘若较为复杂，也不便于计算。因此，需要根据给定点 xi 上的函数值F(xi)，求出一个既能反映F(x)的特性，又便于计算的简单函数ƒ(x)来近似地代替F(x)，此时ƒ(x)称为F(x)的插值函数；x1，x2，…，xn+1，称为插值节点。求插值函数的方法，称为插值法。
多项式是一类简单的初等函数，而且任给两组数：b1，b2，…，bn+1和各不相同的 с1，с2，…，сn+1，总有惟一的次数不超过n的多项式ƒ(x)满足ƒ(сi)=bi，i=1，2，…，n+1。因此在实际应用中常常取多项式作为插值函数。作为插值函数的多项式，称为插值多项式。插值多项式在计算数学插值中最常用。
多元多项式 设α是域F中元素，x1，x2，…，xn是无关的文字。形如
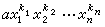(10)的表示式，称为F上x1，x2，…，xn的一个单项式，α称为它的系数，其中k1，k2，…，kn是非负整数，称为文字xi(i=1，2，…，n)的幂指数。 单项式(10)的次数定义为k1+k2+…+kn。两个单项式中如果相同文字的幂指数都相等，那么这两个单项式称为同类项。两个单项式的乘法定义为
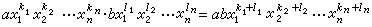。有限个单项式之和称为多元多项式，简称多项式。不同类的单项式之和表示的多项式，其中系数不为零的单项式的最高次数，称为此多项式的次数。
多项式的加法，是指多项式的同类项的系数相加(即合并同类项)。多项式的乘法，是指把一个多项式中的每个单项式与另一个多项式中的每个单项式相乘之后相加，且合并同类项。
F上x1，x2，…，xn的多项式全体所成的集合F[x1，x2，…，xn]，对于多项式的加法和乘法成为一个环，是具有单位元素的整环。
域上的多元多项式也有因式分解惟一性定理。
对称多项式 它在多元多项式中占有重要地位。如果多元多项式ƒ(x1，x2，…，xn)对于1，2，…，n的任一个排列i1，i2，…，in，都有
那么ƒ(x1，x2，…，xn)称为对称多项式。一元多项式根的研究，是对称多项式的来源之一，也是它应用的一个重要方面。以下的n元多项式称为初等对称多项式：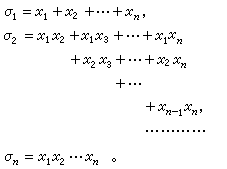
对称多项式的基本定理：x1，x2，…，xn的任一个系数在F中的对称多项式都可表成初等对称多项式σ1，σ2，…，σn的系数在F中的多项式，而且表法是惟一的。
F[x1，x2，…，xn]中所有对称多项式组成F[x1，x2，…，xn]的一个子环。
一元多项式和多元多项式都可以推广到系数属于某个环的情形。特别，系数在数域中的多项式环，是各种环的一类很重要的例子（见环）。