控制理论(卷名:数学)
control theory
研究系统的调节与控制的一般规律的科学。这里叙述的控制理论是指20世纪50年代末至60年代初形成和发展起来的现代控制理论。它现在已成为一门独立的学科,不仅有完整的理论体系,而且已经在诸如工程、生物、生态、社会经济等许多领域有广泛的应用。现代技术特别是现代空间技术的发展是形成控制理论的推动力,数学研究积累的成果为控制理论的形成和发展提供了重要工具,电子计算机的广泛应用使控制理论的成果用于实际成为现实。当前,控制理论为实际系统的描述、分析综合和设计、预测和决策等问题提供了系统的理论和方法。由N.维纳创立的控制论(cybernetic)是一门控制和通信的科学。由Л.C.庞特里亚金、R.贝尔曼、R.E.卡尔曼等人作出了杰出贡献的现代控制理论则是系统科学的一个组成部分,又是形成信息科学的一个基本方面。控制理论涉及的范围很广,它的方向很多。这里就其中几个目前被认为是主要研究内容、并在实际应用中十分广泛的方面作一介绍。
控制理论不是直接研究现实世界中的受控对象,而是研究受控对象的模型。这里说的“模型”是受控对象在一定程度上的数学描述,即数学模型,简称为控制系统。如果描写受控对象的数学模型是线性的,则称为线性控制系统,相仿地有非线性控制系统的称呼。现实世界的受控对象多种多样,例如受控刚体运动与受控弹性体振动两者的受控机制和结果都不一样,有随机因素影响的受控刚体与没有随机因素影响的受控刚体的运动也很不一样,因而描写它们的数学模型的区别就很大。通常,数学模型由常微分方程或差分方程或微分 -差分方程表示的称为集中参数系统;由随机微分方程或随机差分方程表示的称为随机控制系统;而由偏微分方程或偏微分-积分方程表示的称为分布参数控制系统。
线性控制系统理论 它是控制理论的一个重要分支,所研究的对象是线性控制系统,涉及的问题主要有系统描述、能控性和能观测性、极点配置、观测器等内容。
系统描述 线性控制系统是由下列向量微分方程和代数方程描述的。
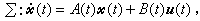 (1)
(1)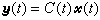 , (2)式中尣(t)、u(t)、у(t)分别是系统
, (2)式中尣(t)、u(t)、у(t)分别是系统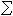 的n维状态向量、r维控制向量、m 维量测向量,记之以尣∈Rn、u∈Rr、у∈Rm,Rn、Rr、Rm分别表示n维、r维、m 维欧几里得空间;A(t)、B(t)、C(t)分别是n×n、n×r,m×n依赖于时间的矩阵。微分方程(1)称为系统的状态方程,它表征了系统状态的动力学特征。代数方程(2)称为系统的量测方程,它反映了系统的内部状态与外部观测之间的关系。当A(t)=A、B(t)=B、C(t)=C,A、B、C全是常值矩阵时,
的n维状态向量、r维控制向量、m 维量测向量,记之以尣∈Rn、u∈Rr、у∈Rm,Rn、Rr、Rm分别表示n维、r维、m 维欧几里得空间;A(t)、B(t)、C(t)分别是n×n、n×r,m×n依赖于时间的矩阵。微分方程(1)称为系统的状态方程,它表征了系统状态的动力学特征。代数方程(2)称为系统的量测方程,它反映了系统的内部状态与外部观测之间的关系。当A(t)=A、B(t)=B、C(t)=C,A、B、C全是常值矩阵时,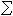 称为定常系统。det[sI-A] 为定常系统∑的特征多项式,det[sI-A]=0为它的特征方程,特征方程的根称为系统的极点。这里I为n×n单位矩阵,s表示复变量,det[·]表示矩阵[·]的行列式。状态方程(1)的t0时刻以尣0=尣(t0)为初态的解可写作:
称为定常系统。det[sI-A] 为定常系统∑的特征多项式,det[sI-A]=0为它的特征方程,特征方程的根称为系统的极点。这里I为n×n单位矩阵,s表示复变量,det[·]表示矩阵[·]的行列式。状态方程(1)的t0时刻以尣0=尣(t0)为初态的解可写作: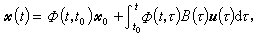 矩阵φ(t,t0)叫做系统
矩阵φ(t,t0)叫做系统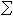 的状态转移矩阵。
的状态转移矩阵。能控性和能观测性 这是由卡尔曼于1960年提出来的两个基本概念,它们刻画了系统
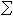 的结构性质。
的结构性质。 如果对在t0时刻任意给定的初态x0,存在某个时刻t1,t1>t0,和定义在时间区间[t0,t1]上的控制输入函数u(t),使得在这个控制作用下,系统
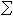 的状态尣(t)满足尣(t1)=On(n维零向量),那么就说系统
的状态尣(t)满足尣(t1)=On(n维零向量),那么就说系统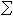 在t0时刻是完全能控的。如果该系统在t≥0的每个时刻都是完全能控的,就说它是完全能控的,简称系统
在t0时刻是完全能控的。如果该系统在t≥0的每个时刻都是完全能控的,就说它是完全能控的,简称系统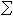 是能控的。系统
是能控的。系统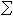 在t0时刻完全能控的充分必要条件是:存在某时刻t1>t0,使得矩阵
在t0时刻完全能控的充分必要条件是:存在某时刻t1>t0,使得矩阵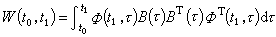 是正定的。当
是正定的。当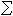 是定常系统时,其能控的充分必要条件是
是定常系统时,其能控的充分必要条件是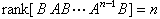 。
。给定初始时刻t0,如果存在某个有限时刻t1,根据时间间隔[t0,t1]上量测输出у(·)和控制输入u(·)能够惟一地决定系统
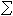 的初态尣(t0),则称
的初态尣(t0),则称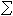 在t0时刻是完全能观测的。如果系统
在t0时刻是完全能观测的。如果系统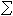 在t≥0的每个时刻都是完全能观测的,则称它是完全能观测的。简称系统
在t≥0的每个时刻都是完全能观测的,则称它是完全能观测的。简称系统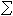 是能观测的。系统
是能观测的。系统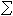 在t0时刻完全能观测的充分必要条件是:存在某个时刻t1>t0,使得矩阵
在t0时刻完全能观测的充分必要条件是:存在某个时刻t1>t0,使得矩阵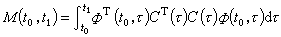 是正定的。当
是正定的。当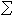 是定常系统时,其能观测的充分必要条件是
是定常系统时,其能观测的充分必要条件是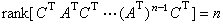 。
。极点配置 对于线性定常系统,它的一些特性(如稳定性、某些动态性质等)主要由其极点决定,因此在设计系统时,要配置极点。设系统
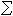 是定常的,如果存在线性状态反馈控制函数u(t)=K尣(t),使闭环系统夶(t)=[A+BK]尣(t)以事先任意给定的n个复数为它的极点,则称系统
是定常的,如果存在线性状态反馈控制函数u(t)=K尣(t),使闭环系统夶(t)=[A+BK]尣(t)以事先任意给定的n个复数为它的极点,则称系统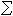 是能任意极点配置的,或者说(A,B)是能任意极点配置的。这里 K是r×n矩阵。定常系统
是能任意极点配置的,或者说(A,B)是能任意极点配置的。这里 K是r×n矩阵。定常系统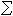 能任意极点配置的充分必要条件是系统完全能控。
能任意极点配置的充分必要条件是系统完全能控。观测器 在系统设计中,由于系统状态常常不能直接量测到,仅依靠状态反馈不能设计出物理上能实现的闭环系统;而能直接量测的是系统的输入u和输出у,所以可以利用系统的量测输出у得到系统的一种估计状态。假如定常系统
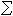 是能观测的,用极点配置的办法可知,存在n×m矩阵G,使A-GC的特征值都具有负实部。于是下列线性定常系统
是能观测的,用极点配置的办法可知,存在n×m矩阵G,使A-GC的特征值都具有负实部。于是下列线性定常系统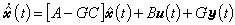 (3)具有性质
(3)具有性质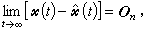 称系统(3)为系统
称系统(3)为系统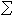 的状态观测器。憫(t)叫做系统
的状态观测器。憫(t)叫做系统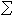 的估计状态。使用估计状态反馈和观测器可以得到系统
的估计状态。使用估计状态反馈和观测器可以得到系统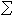 的一个动态补偿器
的一个动态补偿器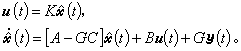 由此得到的闭环系统
由此得到的闭环系统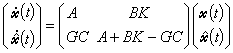 是渐近稳定的。
是渐近稳定的。最优控制理论 是控制理论中最早发展的分支之一。对于控制系统,常常要求找到控制函数,在它的作用下,系统从一个状态转移到所希望的状态,并且还希望控制方式是最好的。这就是最优控制问题。
问题的提法 设有非线性受控系统,它由下列非线性向量微分方程描述
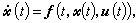 (4)这里,控制向量u通常不能任意取值,它受有限制,用u属于Rr中某个有限闭区域Ur来表示,即
(4)这里,控制向量u通常不能任意取值,它受有限制,用u属于Rr中某个有限闭区域Ur来表示,即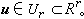 设x0是给定的初态,xƒ是控制作用结束或控制过程结束时系统(4)的状态,简称为终端状态或末状态。它可以是自由的,也可以是受限制的。用定义在某U上的泛函
设x0是给定的初态,xƒ是控制作用结束或控制过程结束时系统(4)的状态,简称为终端状态或末状态。它可以是自由的,也可以是受限制的。用定义在某U上的泛函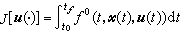 (5)来表示控制方式的优劣,称为系统(4)的性能指标。其中t0、tƒ分别是控制过程的初始时刻和终止时刻(可以是事先指定的,也可以是待求的),U是定义在有限时间区间上、把系统(4)的t0时刻的状态x0转移到tƒ时刻的状态xƒ、并在Ur中取值的控制函数u(t)的全体,称为容许控制函数集合。尣(t)是系统(1)的相应于u(t)的解。ƒ0(t,尣,u)是t,尣,u的已知函数。所谓最优控制问题是指在U中寻找一个控制函数,使(5)中J[u(·)]取极小(或极大)。如果使J[u(·)]取极小(或极大)的控制函数存在,记为u*(t),称它为(4)、(5)的最优控制。在u*(t)的作用下,系统(4)的t0时刻以x0为初态的解尣*(t)称为(4)、(5)的最优轨线,对应于u*(t)、尣*(t)的性能指标值
(5)来表示控制方式的优劣,称为系统(4)的性能指标。其中t0、tƒ分别是控制过程的初始时刻和终止时刻(可以是事先指定的,也可以是待求的),U是定义在有限时间区间上、把系统(4)的t0时刻的状态x0转移到tƒ时刻的状态xƒ、并在Ur中取值的控制函数u(t)的全体,称为容许控制函数集合。尣(t)是系统(1)的相应于u(t)的解。ƒ0(t,尣,u)是t,尣,u的已知函数。所谓最优控制问题是指在U中寻找一个控制函数,使(5)中J[u(·)]取极小(或极大)。如果使J[u(·)]取极小(或极大)的控制函数存在,记为u*(t),称它为(4)、(5)的最优控制。在u*(t)的作用下,系统(4)的t0时刻以x0为初态的解尣*(t)称为(4)、(5)的最优轨线,对应于u*(t)、尣*(t)的性能指标值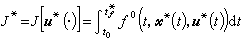 称为最优指标值,而t壚是最优过程终止的时刻。
称为最优指标值,而t壚是最优过程终止的时刻。极大值原理 这是1958年由Л.С.庞特里亚金等人提出的,它是最优控制满足的必要条件。这里就下列特殊情况来叙述,即:①(4)、(5)中的ƒ及ƒ0不显含时间t;②对U中任一控制函数u(t),ƒ(尣,u(t))满足使(4)的初值问题的解存在惟一性条件;③终端状态xƒ受形如g(xƒ)=0的约束,g(尣)是尣的连续可微分标量函数,且
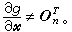 定义系统(4)和性能指标(5)的哈密顿函数h(尣,ψ0,Ψ,u)为:
定义系统(4)和性能指标(5)的哈密顿函数h(尣,ψ0,Ψ,u)为: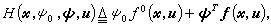 又
又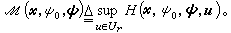 极大值原理的内容是:如果u*(t)是(4)、(5)的最优控制,x*(t)是 (4)、(5)的最优轨线,那么必定存在非零函数ψ0(t)、Ψ(t),它们和u*(t)、尣*(t)一起在[t0,t壚]上满足:
极大值原理的内容是:如果u*(t)是(4)、(5)的最优控制,x*(t)是 (4)、(5)的最优轨线,那么必定存在非零函数ψ0(t)、Ψ(t),它们和u*(t)、尣*(t)一起在[t0,t壚]上满足:①
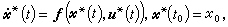
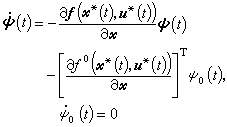 在[
在[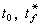 ]上除有限个时刻外处处成立。ψ0,Ψ叫做(4)、(5)的共轭变量或协态,它们满足的微分方程叫做共轭方程。
]上除有限个时刻外处处成立。ψ0,Ψ叫做(4)、(5)的共轭变量或协态,它们满足的微分方程叫做共轭方程。② 在[
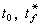 ]上成立
]上成立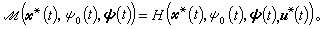
③ 当
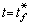 时,有
时,有 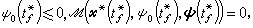
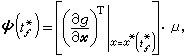 μ为非零的待定常数。
μ为非零的待定常数。又,如果①、②成立,则
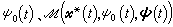 在区间[
在区间[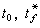 ]上恒等于常数。
]上恒等于常数。极大值原理包含了为确定u(t)、尣(t)、ψ0(t)、Ψ(t)的全部关系式,但要具体确定出这些函数并不容易。当ƒ(尣 ,u)是尣、u的线性函数(即(4)是线性定常系统)且J[u(·)]是工程实际中有意义的特殊性能指标时,从极大值原理可以惟一地确定出最优控制和最优轨线。
时间最优控制(快速控制)问题 即
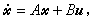 (6)
(6)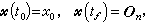 (7)
(7)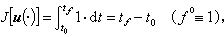 (8)
(8)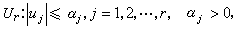 式中
式中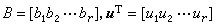 表示u的行向量。如果,①U非空;②
表示u的行向量。如果,①U非空;②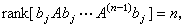
 则系统(6)的把x0转移到尣(t壚)=On的时间最优控制
则系统(6)的把x0转移到尣(t壚)=On的时间最优控制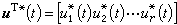 存在且惟一,并具有下列形式
存在且惟一,并具有下列形式 式中sgn(·)表示(·)的符号函数;μT是待求的n维的行向量。
式中sgn(·)表示(·)的符号函数;μT是待求的n维的行向量。线性二次最优控制(LQ)问题 即
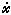 =Ax+Bu, (9)
=Ax+Bu, (9)尣(t0)=x0,尣(tƒ)自由, (10)
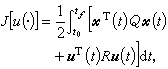 (11)式中Q是n×n非负定对称矩阵;R是r×r正定对称矩阵,tƒ 固定。由极大值原理知(9)、(10)、(11)的最优控制u*(t)和最优轨线尣*(t)满足
(11)式中Q是n×n非负定对称矩阵;R是r×r正定对称矩阵,tƒ 固定。由极大值原理知(9)、(10)、(11)的最优控制u*(t)和最优轨线尣*(t)满足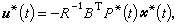 式中P*(t)是下列黎卡提矩阵微分方程终值问题
式中P*(t)是下列黎卡提矩阵微分方程终值问题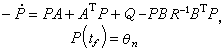 的n×n非负定矩阵解,其中θn为n×n零方阵。
的n×n非负定矩阵解,其中θn为n×n零方阵。非线性控制理论 是现代控制理论中较晚发展起来的一个分支,60年代末发展起来,70年代以后愈来愈多地为人们所重视。与线性系统理论相似,能控性、能观测性、稳定性、调节问题、系统解耦问题、干扰解耦问题、最优控制问题、微分对策问题等等是它研究的重要内容。不同的是,近年来,分岔、失稳与控制、混沌等问题也出现在非线性控制理论的研究领域内。非线性控制系统由下列非线性向量微分方程和非线性函数方程描述,
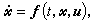 (12)
(12)у=H(t,尣,u), (13)式中t、u、尣、у的意义同前;ƒ、H是t、尣、u的非线性向量函数。(12)描述了非线性控制系统状态x的动力学特征,(13)表示系统状态尣、控制输入u与量测输出у之间的非线性关系。
能控性问题 对于非线性定常控制系统
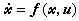 , (14)
, (14)如果存在r维向量控制函数u(t),使(14)的t0时刻以x0为初态的解尣(t,x0)在某时刻t1(t1>t0)满足
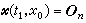 ,则称x0是系统(14)的能控状态;如果Rn中每个尣都是(14)的能控状态,则称系统(14)是完全能控的。如果Rn中某区域D内的每个尣都是(14)的能控状态,则说系统(14)在D内是能控的。如果系统(14)在原点尣=On的某邻域内是能控的,则称它是局部能控的。
,则称x0是系统(14)的能控状态;如果Rn中每个尣都是(14)的能控状态,则称系统(14)是完全能控的。如果Rn中某区域D内的每个尣都是(14)的能控状态,则说系统(14)在D内是能控的。如果系统(14)在原点尣=On的某邻域内是能控的,则称它是局部能控的。设(14)中ƒ 是尣,u的二次连续能微分向量函数,且
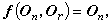 记
记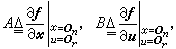 如果秩条件
如果秩条件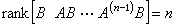 成立,则系统(14)是局部能控的。当贝尔曼型偏微分方程
成立,则系统(14)是局部能控的。当贝尔曼型偏微分方程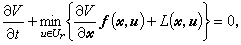 (15)
(15)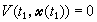 , (16)在Rn中存在正定解时,非线性控制系统(14)是完全能控的,并且(14)的以
, (16)在Rn中存在正定解时,非线性控制系统(14)是完全能控的,并且(14)的以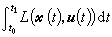 为性能指标的最优控制函数存在。这里l(尣,u)是某个给定的在Rn×Ur上定义的正定标量函数,t1是某个大于零的时刻。
为性能指标的最优控制函数存在。这里l(尣,u)是某个给定的在Rn×Ur上定义的正定标量函数,t1是某个大于零的时刻。调节问题 对于非线性控制系统(14),如果存在依赖于状态x的控制函数u(尣),使得将u(尣)代入(14)后得到的系统──闭环系统
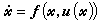 (17)是渐近稳定系统,则称系统(14)是能调节的;如果(17)是全局渐近稳定的,则说系统(14)是全局能调节的;如果(17)在包含原点尣=On为内点的某区域Ω内是渐近稳定的,则称(14)在Ω内是能调节的;如果(17)在原点尣=On的某领域内是渐近稳定的,则称(14)是局部能调节的。这样的控制函数u(尣)叫做(14)的非线性状态反馈,又叫做(14)的调节器。
(17)是渐近稳定系统,则称系统(14)是能调节的;如果(17)是全局渐近稳定的,则说系统(14)是全局能调节的;如果(17)在包含原点尣=On为内点的某区域Ω内是渐近稳定的,则称(14)在Ω内是能调节的;如果(17)在原点尣=On的某领域内是渐近稳定的,则称(14)是局部能调节的。这样的控制函数u(尣)叫做(14)的非线性状态反馈,又叫做(14)的调节器。设(14)中ƒ 是尣,u的二次连续能微分向量函数,且ƒ(On,Or)=On,如果秩条件
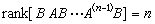 成立(A,B的意义同前),则非线性系统(14)是能局部调节的。如果贝尔曼型偏微分方程
成立(A,B的意义同前),则非线性系统(14)是能局部调节的。如果贝尔曼型偏微分方程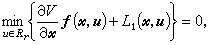 (18)
(18)V(On)=0 (19)在Rn中存在正定解,则非线性控制系统(14)是全局能调节的。这里l1(尣,u)是定义在Rn×Rr中的正定标量函数,且当
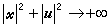 时,
时,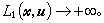
自70年代以来,R.W.布劳克特、H.J.萨斯曼、H.赫姆斯、B.雅库布奇乌克等人运用李代数、微分几何等数学工具研究流形上的非线性控制系统,在系统的能控性、能观测性、可逆性、系统的干扰解耦、最优控制等方面得到了很有启发性的结果。同时,人们还研究了通过非线性坐标变换和非线性状态反馈将一类非线性控制系统(如双线性系统)局部地或全局地变换为线性系统的问题,从而能够利用线性系统的理论和方法进行讨论。
随机控制系统 是指带有随机干扰的动态系统,对它的主要研究内容有系统辨识、适应控制、状态滤波和随机控制。
系统辨识 对一个客观的物理系统,为了控制它或预测它的发展,必先根据系统的输入和输出建立起它的数学模型,这就是系统辨识。如果用随机差分方程来描述要辨识的动态系统:
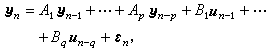 (20)则系统辨识的任务就是依据输入{uk}及输出{уk}来估计系统的阶数(p,q)、系统的未知参数
(20)则系统辨识的任务就是依据输入{uk}及输出{уk}来估计系统的阶数(p,q)、系统的未知参数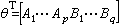 以及系统噪声εn中可能出现的未知参数。当系统的阶数已知,并且不计εn中的未知参数时,动态系统(20)变成线性回归模型
以及系统噪声εn中可能出现的未知参数。当系统的阶数已知,并且不计εn中的未知参数时,动态系统(20)变成线性回归模型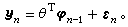 (21)但它不同于数理统计学中经典的线性模型,因为这里的
(21)但它不同于数理统计学中经典的线性模型,因为这里的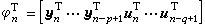 是随机的。
是随机的。对θ的估计,最常用的是最小二乘法,在n+1时刻,它表达为
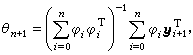 并且可以递推地计算。如果εn是一个滑动平均过程εn=
并且可以递推地计算。如果εn是一个滑动平均过程εn=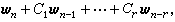 其中Ci(i=1,…,r)也要估计,那么只要把θ和φn相应地扩大为
其中Ci(i=1,…,r)也要估计,那么只要把θ和φn相应地扩大为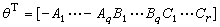 ,
, 最小二乘辨识的公式仍可用。使θn收敛到θ的条件,收敛速度,对系统阶数的估计等都是系统辨识研究的内容。
最小二乘辨识的公式仍可用。使θn收敛到θ的条件,收敛速度,对系统阶数的估计等都是系统辨识研究的内容。适应控制 如果不仅参数 θ未知,同时又要按一定性能指标选控制作用{un}(前述的,对输入un没有要求),这就是适应控制。最简单的一种是适应跟踪,即:θ 未知,并要选{un}使输出уn尽可能好地跟踪一个已知的确定性讯号у奱。从(21)可以看出,当噪声 εn不能预报时,对уn的最优预报是
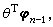 但θ是未知参数,只知道对它的估计值θn-1,所以对уn可采用的预报值是
但θ是未知参数,只知道对它的估计值θn-1,所以对уn可采用的预报值是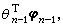 为了使уn与у奱的差别尽可能地小,很自然地要选un-1使
为了使уn与у奱的差别尽可能地小,很自然地要选un-1使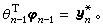 这样选取的适应控制,可使系统在下列意义下稳定:
这样选取的适应控制,可使系统在下列意义下稳定: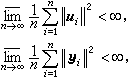 并且跟踪误差可以渐近地达到最小。当у奱取不依赖于n的常值时,适应跟踪器通常叫做自校正调节器。
并且跟踪误差可以渐近地达到最小。当у奱取不依赖于n的常值时,适应跟踪器通常叫做自校正调节器。适应控制也考察比跟踪问题更一般的指标。
状态滤波 上面讨论的是输入输出模型,没有把中间状态的发展情况刻画出来。实际的随机系统经常用一对随机差分方程来描述,即状态尣k的转移方程
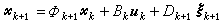 (22)和量测方程(它可能只观测部分状态,而不是全部尣k)
(22)和量测方程(它可能只观测部分状态,而不是全部尣k)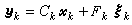 (23){ξk}表示系统的随机干扰。当系统的系数矩连Фk、Bk、Dk、Ck、Fk已知时,状态滤波就是用量测量(у0,…,уk)求 尣k的最小方差估计(见点估计)憫k。 憫k的递推表达式叫卡尔曼滤波(见滤波):
(23){ξk}表示系统的随机干扰。当系统的系数矩连Фk、Bk、Dk、Ck、Fk已知时,状态滤波就是用量测量(у0,…,уk)求 尣k的最小方差估计(见点估计)憫k。 憫k的递推表达式叫卡尔曼滤波(见滤波):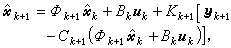 它的前两项是依状态方程来发展的,最后一项是修正项,Kk叫增益矩阵,它可以递推地计算。当系统的系数矩阵为常矩阵时,Kk可能趋于常矩阵,这时就得到稳态滤波器,它便于计算。
它的前两项是依状态方程来发展的,最后一项是修正项,Kk叫增益矩阵,它可以递推地计算。当系统的系数矩阵为常矩阵时,Kk可能趋于常矩阵,这时就得到稳态滤波器,它便于计算。对连续时间的非线性系统,滤波方程由无穷个随机微分方程组成,一般只能近似求解,但对条件正态过程,它是封闭的方程组。对线性系统,滤波方程叫卡尔曼-布西滤波。
随机控制 对系统(20)、(21)或(22)、(23),设系数矩阵已知,uk只依赖于过去的量测,并要使某一性能指标达最小,这就是随机控制问题。对此,解决得最完整的是二次性能指标。对系统(22)、(23),就是要使
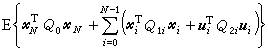 达最小,
达最小,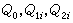 为非负定矩阵,E为数学期望。当{ξk}为零均值的不相关随机向量时,最优控制是
为非负定矩阵,E为数学期望。当{ξk}为零均值的不相关随机向量时,最优控制是 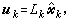 憫k就是上面得到的滤波值,lk是反馈增益,它就是系统退化为确定性系统时,二次指标下最优控制的反馈增益。这个事实叫分离原理。对连续时间系统,尽管有随机极大值原理,但除了二次指标问题已解决外,其他方面实质性的结果不多。
憫k就是上面得到的滤波值,lk是反馈增益,它就是系统退化为确定性系统时,二次指标下最优控制的反馈增益。这个事实叫分离原理。对连续时间系统,尽管有随机极大值原理,但除了二次指标问题已解决外,其他方面实质性的结果不多。分布参数控制系统 现代控制理论的一个重要分支,研究的对象是用偏微分方程或偏微分-积分方程描述的系统。例如,描述温度场、弹性振动、核反应堆等系统都是分布参数系统。它同前面讲的用常微分方程描述的集中参数系统不同,其状态空间是某一个函数空间,在每一瞬间的状态是函数空间中的一个函数。这就是说,系统在每一瞬时的状态,不能用有穷个参数来确定,必须用无穷个参数才能确定。研究这类系统需要用泛函分析、现代偏微分方程理论等现代数学工具。
分布参数系统研究的内容是系统的辨识、系统的滤波和系统的控制。
分布参数系统的辨识,从某种意义上讲也是一种建立模型。辨识研究的问题是一个分布参数系统的结构已知,但这个系统有一部分是未知的,对该系统的某些物理量进行量测(这些物理量含有未知部分的信息),依据这些量测量来确定出系统的未知部分。辨识问题在工程、技术中很多也很重要。
例如,油田在开发过程中,油的压力变化规律用下面的偏微分方程来描述:
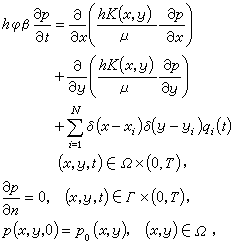 式中p(x,y,t)表示在t时刻坐标为(x,y)点处油的压力,h是油层的厚度,μ是石油的粘度,β是压缩系数,qi(t)是第i口井的产量密度,(xi,yi)是第i口油井位置坐标,Ω是油储区域,Г是油层区域的边界,φ是孔隙度,K(x,y)是渗透系数,未知的地质参数。
式中p(x,y,t)表示在t时刻坐标为(x,y)点处油的压力,h是油层的厚度,μ是石油的粘度,β是压缩系数,qi(t)是第i口井的产量密度,(xi,yi)是第i口油井位置坐标,Ω是油储区域,Г是油层区域的边界,φ是孔隙度,K(x,y)是渗透系数,未知的地质参数。在打井的位置(xi,yi)(i=1,2,…,N)可以直接得到K(xi,yi),但是在油田的其他点处,不能直接得到K(x,y),通过在每口井处量测的压力和流量来确定出渗透率K(x,y),掌握了K(x,y)的变化规律,就可以了解油田每口井的产量的变化。
辨识出系统的未知部分后,系统就完全确定。如果外部随机干扰对系统有影响,还需要对系统进行滤波,以减少噪声对系统的影响。系统经过辨识和滤波后,如果还需要选择系统的某些参数,使其具有人们需要的某种最好的性能,这就是最优控制问题。
例如,一细长的金属杆一端加热,热量在杆中的传导服从下面的热传导方程:
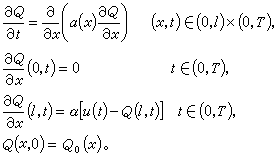 式中Л是金属杆长度,α(x)是热传导系数,u(t)是未知函数,称为控制量。问题是要选择一种加温方法,即选择一控制函数0≤u(t)≤A(A为常数),使得加温到T时刻,金属杆中的温度分布为所要求的温度分布Q*(x),也就是选择一个u*(t),使得泛函
式中Л是金属杆长度,α(x)是热传导系数,u(t)是未知函数,称为控制量。问题是要选择一种加温方法,即选择一控制函数0≤u(t)≤A(A为常数),使得加温到T时刻,金属杆中的温度分布为所要求的温度分布Q*(x),也就是选择一个u*(t),使得泛函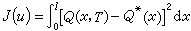 达到极小,即
达到极小,即