热容(卷名：化学)
heat capacity
物质的热力学性质之一，热力工程设计和过程热平衡计算的基础热数据。在任一过程中，加给体系的热量与体系由此发生的温度的变化之比，被定义为体系的热容。它又分为真热容和平均热容。在温度T时的真热容C相应于一个无限小的温度变化：
相应于有限的温度变化：
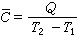(2)式中Q为把体系从T1加热到T2所需要的热量。热容的这种定义，适用于任何体系（单组分或多组分的；单相的或多相的）。物理化学中常指由单组分组成的单相体系。若体系的质量为1千克，则其热容称为比热容或比热c，若质量为1摩尔，则称摩尔热容C。显然，比热容和摩尔热容可以是真热容也可以是平均热容，它们的关系为：
(3)比热容的单位是焦/(千克·开)，而摩尔热容的单位则是焦/(摩尔·开)。定容热容和定压热容 由于热量δQ与过程的途径有关，必须指出决定途径的条件，热容才有确定的值。化学热力学中最常用的是等容和等压过程，在等容下得到摩尔热容
；在等压下得到摩尔热容
。在等容过程和等压过程中，对无限小的变化来说，根据热力学第一定律可以得到 δQV＝dU和 δQp＝dH，式中dU和dH分别为体系内能和焓的变化。由此得到摩尔热容、内能与焓相关联的表达式：
(4)
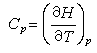(5)由上式可知，定容热容等于体积不变时内能随温度的变化率；定压热容等于压力不变时焓随温度的变化率。这两个关系式既可用于纯物质，也可用于恒组成的任意均相体系。
Cp和CV具有一定的关系，Cp恒大于CV。因为物质在等压下加热时，做了压力－体积功，故Cp与CV之差值，就等于等压过程中体系对外界所做的膨胀功。热力学第一定律给出了这一差值的精确表达式：
(6)
(7)式中V 是物质的摩尔体积；β 为等压体膨胀系数，β＝
；KT为等温压缩系数，
。β、KT、V、Cp均可由实验测出，利用式(7)可计算出CV。对于理想气体，可由式(6)导出：
Cp-CV＝R (8)式中R为气体常数。
气体的定压热容与定容热容之比称为热容商，用γ表示：
γ＝Cp/CV (9)
在中等压力下，单原子气体的 CV约为3R/2，γ约为1.67，CV随T 的变化很小。对于双原子气体，在室温和中等压力下，CV近似为5R/2，γ为1.42～1.40，CV随T的变化通常较小。对于三原子气体，在适当压力下，CV约从3R变化到3.5R；CV随T的变化较大，γ也变小。对于含有三个以上原子的气体，不能归纳出一般性的结论。但当分子的复杂性增加时，热容也随之增加，温度对热容的影响也加大，而γ则减小。
在几个大气压之内，压力对气体热容的影响很小，通常可以忽略。
固体热容的经验定律 杜隆－珀替摩尔原子热容定 律 其内容为：在室温下固体单质的定压热容Cp近似等于6.2卡/（摩尔·开），例如金的Cp为6.0，镍为6.2，铅为6.4。但对于原子量低于39的某些轻元素，误差可能很大。例如，碳（石墨）的Cp为2.1，硼为2.9，硅为4.8。
柯普－诺伊曼化合物热容加和定律 其内容为：在室温和常压下，一个化合物的摩尔热容近似等于组成该化合物的元素摩尔原子热容之和，即化合物的热容Cp≈6.2n，式中n为分子中的原子数。例如，氯化锂的Cp计算值为12.4，实测值为12.2。但例外的情况也很多，误差也比较大。
经典动力学根据能量均分原理对上述两个定律作了理论解释。按照这一原理，1摩尔物质在每一个运动自由度上分配的热容CV等于R/2，固体晶格中的原子和离子取六个自由度（其中三个是动能的，另外三个是势能的），所以对1摩尔原子而言，CV=6·(R/2)=3R，即近似为6卡/（摩尔·开），这就是杜隆－珀替定律。对于由n个原子组成的化合物，则为：
CV＝3nR≈6n这就是柯普－诺伊曼定律。
上述经验定律没有反映热容与温度的关系。实验表明，热容是温度的函数，温度是影响热容最重要的参数，几乎所有物质的热容都随温度升高而增加。分子结构愈复杂，热容随温度升高得愈快。在不同温度范围内，热容随温度变化的情形也不同。以国际上通用的热容标准物质α－氧化铝为例，在10K时，Cp＝0.009焦/(摩尔·开)，100K时，Cp＝12.855;300K时，Cp＝79.41；1000K时，Cp＝124.77;1500K时，Cp＝132.29。若以10K的Cp为基数，则后面四个温度的Cp的增加倍数分别为1.4×103、8.8×103、1.4×104和1.5×104。由此可见，热容随温度的变化是很显著的。对于晶体物质，其热容随温度变化的一般规律是：在绝对零度附近，热容与T3成正比，接着出现一直线部分，然后在高温时接近杜隆－珀替定律规定的值。
德拜热容理论 经典理论不能解释热容随温度变化的实验事实。A.爱因斯坦、W.H.能斯脱、F.A.林德曼和P.德拜等人力图从量子理论出发，来说明热容随温度的变化规律。其中以德拜热容理论最为成功。德拜把晶体里的原子当作振动子，如果有N个原子，振动子的数目就是 3N，它们的振动频率v不一致，有低有高，但不超过一最高值vm。德拜假设晶体是一种连续介质，晶体里的振动过程和声波通过弹性介质所发生的振动的情形相似。根据这个假设，德拜推导出一个复杂的数学公式：
(10)式中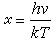
；
；h为普朗克常数;k为玻耳兹曼常数;θD具有温度量纲，包含有物质特有的晶格原子振动的极限频率vm，故称德拜特征温度。在足够低的温度(T《θD)时，式(10)可化简为：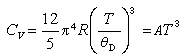
(11)上式称为德拜低温晶体热容 T立方公式。此式通常只在T＜(θD/50)的温度范围内适用。由式(11)可知，热容CV是T/θD的单值函数，当无量纲值T/θD相等时，各种物质的热容也相同。这样根据各种物质的 θD值，利用德拜函数表
即可直接计算热容值。θD可以从光谱数据计算，也可由低温热容实验测定。它随物质而异，通常在100～400K范围内。例如，铅为 88；汞为100；金为170；银为215；铜为315;铝为398；铁为420；但金刚石为1860，这是由于它的特殊结构所引起的。在高温(T》θD)时，式(10)可化简为：CV＝3R。这与经典理论一致，因此德拜理论可以较好地解释晶体热容与温度的关系，算出的CV值与实验曲线也相符合。
液体的热容 尚无实用的理论。在液体里，分子运动可以分为平动、转动和振动三种，但每种运动都受分子间作用力的影响。这种分子间作用力由各种液体的特性所决定，因而使理论处理变得十分复杂和困难。一般来说，同一种物质的液态热容比固态热容稍高，随温度的变化也较小。
实用上，温度对热容的影响常用各种函数式表达。例如，从室温到1500K，是化学反应工程的很重要的温度范围，在此区间内热容与温度的关系多用下列形式的经验方程式表示：
应用 许多在理论和实际上有用的热力学计算都是以物质的热容数据为基础的。例如，要计算不同温度下物质的特征热力学函数焓、熵、自由能时，最有效的途径就是在很宽的温度范围内直接测量物质的热容。化学热力学中计算反应热随温度的变化，准确求出平衡常数同温度的关系以及根据热力学第三定律计算绝对熵，都需要可靠的热容数据作依据。此外，由于热容是物质非常灵敏的性质，它对研究物质结构、物质中分子或原子之间的相互作用、相变和临界现象，测定物质中微量杂质含量以鉴定纯度等方面也起着特殊作用。在化学和冶金工业方面，例如计算反应器、高炉等的热平衡时，有关的纯物质及其混合物的热容数据就是不可缺少的基本参数。在尖端科学技术方面，例如在人造卫星、航天飞机的防热设计中，就需要应用大量的有关各种复合材料的热容数据。
热容的测定 气体热容的测定法有：①直接量热法，例如气体流动量热法。②大多数气体热容都是从光谱数据用统计力学的方法计算出的。固体和液体的热容数据几乎都是用量热法测定的。由于测量温区、被测物质和要求的精度不同，所采用的量热方法和量热计的类型也不同，其中使用最多、精度最高的是低温真空绝热量热计(图1 )
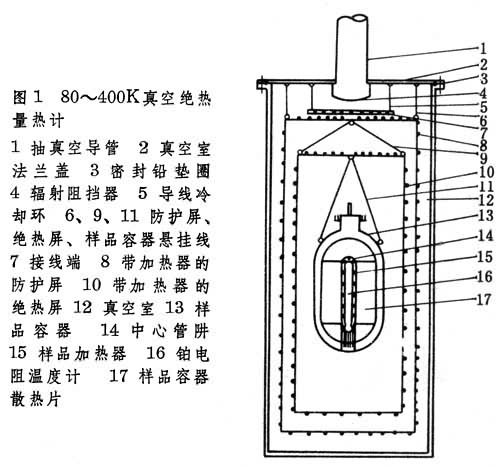和高温落入式铜块量热计（图2）。
能斯脱设计的真空卡计和R.W.本生设计的冰量热计是这两种类型量热计的最初模式，到20世纪中期已发展得比较完善，前者用于10～550K时测定物质的真热容，精度达0.1％～0.05％;后者用于400～3000K时测定平均热容，精度达1％～0.5％。真空绝热量热计的简单工作原理是：将量热计的真空室抽成高真空后，向样品通入一定量电能Q，使其温度升高ΔT，与此同时严格控制绝热屏温度，使之与样品容器的温度相等。这样，试样与环境之间就维持绝热条件，通入的电能完全被样品吸收。试样的比热容可根据cp＝Q/(ΔT·m)式求出，式中m为试样的质量。
落入式铜块量热计的工作原理是：先将试样置于高温炉内加热到某一温度T，然后让其落入到处于室温或水的冰点温度T0的铜块量热计内。由于试样放热而使铜块温度上升ΔT′，根据量热计的能当量A便可求出T0～T温度范围内试样的平均比热容:
参考书目
J.P.McCullough and D.W.Scott，ed.，Experimental Thermodynamics， Vol.1，Butterworths， London， 1968.