分子轨道理论(卷名:化学)
molecular orbital theory
一种化学键理论,是原子轨道理论对分子的自然推广。其基本观点是:物理上存在单个电子的自身行为,只受分子中的原子核和其他电子平均场的作用,以及泡利不相容原理的制约;数学上则企图将难解的多电子运动方程简化为单电子方程处理。因此,分子轨道理论是一种以单电子近似为基础的化学键理论。描写单电子行为的波函数称轨道(或轨函),所对应的单电子能量称能级。对于任何分子,如果求得了它的系列分子轨道和能级,就可以像讨论原子结构那样讨论分子结构,并联系到分子性质的系统解释。有时,即便根据用粗糙的计算方案所得到的部分近似分子轨道和能级,也能分析出很有用处的定性结果。

氢分子离子的分子轨道 正如在原子轨道理论中,氢原子的严格解提供了进一步发展的理论模式,氢分子离子H娚中,单个电子在固定核间距R的双质子场中的波动方程解,是分子轨道理论进程中的基石。H娚的分子轨道用符号σ、π、
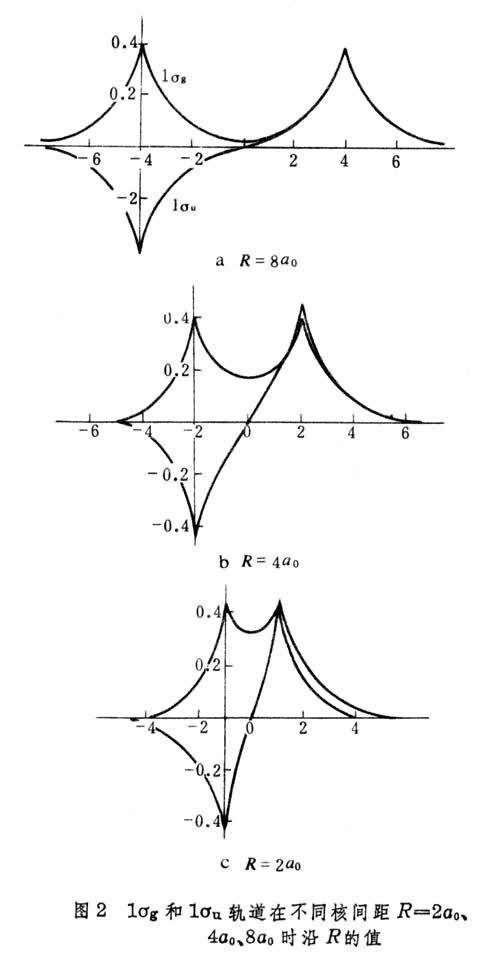
 、…表征,对应于精确解中的量子数m=0,±1,±2,…,它描述相对于核间距R的轨道对称行为。此外,还需用g和u表征相对于分子中心反演的对称行为。综合起来,H娚的分子轨道用σg、σu、πg、πu、…等符号表征,借助精确求解固定核间距R的波动方程获得。图1给出两个最低轨道1σg和1σu的能量E随R的变化曲线。1σg能级有一极小值-1.20Ry(里德伯能量),出现在R=2a0处(a0为玻尔半径,图2),代表基态;当R增大以至无穷时, 1σg能量趋近-1.0Ry。两者差值0.20Ry就是H娚的离解能。1σu的行为不同, 能量随R减小而单调上升,显示排斥态的本质。1σg和1σu也被称作成键轨道和反键轨道。1σg均取正值,1σu则在中心两端发生符号变化,但极值均出现在质子所在处,且伴随R变小;1σg在核间区数值增大,描写了电子在分子中的转移。随着R的增大,1σg和1σu的函数值渐近于式(1)~(2):
、…表征,对应于精确解中的量子数m=0,±1,±2,…,它描述相对于核间距R的轨道对称行为。此外,还需用g和u表征相对于分子中心反演的对称行为。综合起来,H娚的分子轨道用σg、σu、πg、πu、…等符号表征,借助精确求解固定核间距R的波动方程获得。图1给出两个最低轨道1σg和1σu的能量E随R的变化曲线。1σg能级有一极小值-1.20Ry(里德伯能量),出现在R=2a0处(a0为玻尔半径,图2),代表基态;当R增大以至无穷时, 1σg能量趋近-1.0Ry。两者差值0.20Ry就是H娚的离解能。1σu的行为不同, 能量随R减小而单调上升,显示排斥态的本质。1σg和1σu也被称作成键轨道和反键轨道。1σg均取正值,1σu则在中心两端发生符号变化,但极值均出现在质子所在处,且伴随R变小;1σg在核间区数值增大,描写了电子在分子中的转移。随着R的增大,1σg和1σu的函数值渐近于式(1)~(2):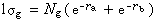 (1)
(1)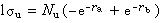 (2)式中Ng和Nu是归一化系数;
(2)式中Ng和Nu是归一化系数;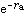 和
和 分别是两个组成氢原子上的 1s原子轨道。图3
分别是两个组成氢原子上的 1s原子轨道。图3 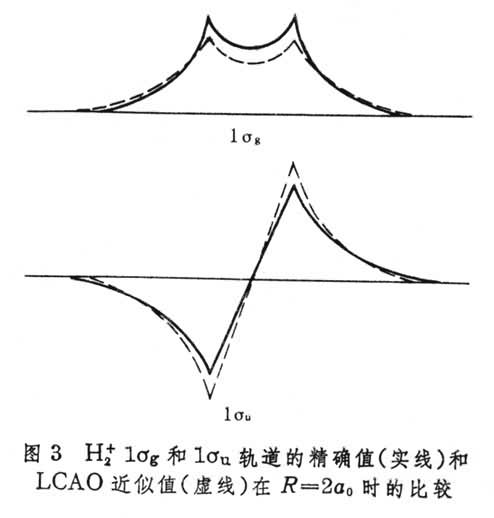 给出R=2a0时,1σg和1σu轨道的精确值和按式(1)与(2)的近似值的比较,说明式(1)与(2)的近似程度是很好的。式(1)和(2)表示,分子轨道可以近似地当作原子轨道的线性组合,简写为LCAO(见量子化学计算方法)。当R很大时,结果是准确的,即使R达到分子核间距大小时,也给出不错的结果。这一点启发了对复杂分子也可采用LCAO方法去寻找近似分子轨道。这是因为在分子中,靠近一个核的电子主要受到该核的势场的作用;而受到其余核的联合作用,则小得多,因此在近核处,分子轨道必定近似于该核的原子轨道。对于整个空间的任何一点,可以设想分子轨道由有关的原子轨道线性组合而成。一般的形式是:
给出R=2a0时,1σg和1σu轨道的精确值和按式(1)与(2)的近似值的比较,说明式(1)与(2)的近似程度是很好的。式(1)和(2)表示,分子轨道可以近似地当作原子轨道的线性组合,简写为LCAO(见量子化学计算方法)。当R很大时,结果是准确的,即使R达到分子核间距大小时,也给出不错的结果。这一点启发了对复杂分子也可采用LCAO方法去寻找近似分子轨道。这是因为在分子中,靠近一个核的电子主要受到该核的势场的作用;而受到其余核的联合作用,则小得多,因此在近核处,分子轨道必定近似于该核的原子轨道。对于整个空间的任何一点,可以设想分子轨道由有关的原子轨道线性组合而成。一般的形式是:
任意双原子分子的分子轨道 用原子轨道线性组合法LCAO近似来讨论任意双原子分子中,分属两个原子的一对原子轨道形成分子轨道的最优条件。这时,式(3)采取以下简单形式: ψ=c1φa+c2φb (4)代入波动方程Hψ=Eψ,得到近似能级E:  (5)式中Haa和Hbb分别是原子轨道φa和φb的库仑积分,可看作φa和φb的能量,即Haa=Ea,Hbb=Eb;Hab=β称共振积分,与φa和φb的重叠情况有关,一般取负值,Sab称重叠积分,可当作零处理,而不影响定性结论。最优条件由E取极值确定,即: (5)式中Haa和Hbb分别是原子轨道φa和φb的库仑积分,可看作φa和φb的能量,即Haa=Ea,Hbb=Eb;Hab=β称共振积分,与φa和φb的重叠情况有关,一般取负值,Sab称重叠积分,可当作零处理,而不影响定性结论。最优条件由E取极值确定,即: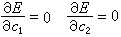 (6)上式给出一组c1、c2的齐次方程组,由系数组成的久期方程(见休克尔分子轨道法)得到: (6)上式给出一组c1、c2的齐次方程组,由系数组成的久期方程(见休克尔分子轨道法)得到: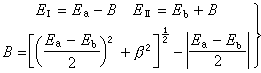 (7)设Ea<Eb,则式(7)的含意可用图4 表示。 (7)设Ea<Eb,则式(7)的含意可用图4 表示。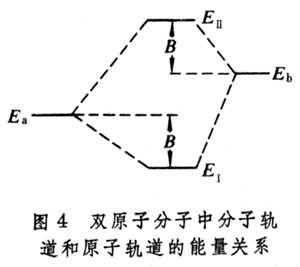 由此看出,有效的成键作用决定于B值的大小,后者又与原子轨道能量差|Ea-Eb|以及重叠情况β有关,从而可归纳为三个条件: ① 能量近似条件:指|Ea-Eb|越小越好,当|Ea-Eb|=0时,B最大,等于|β|。 ② 最大重叠条件:φa与φb的重叠越大(图5),β的绝对值也可能越大。 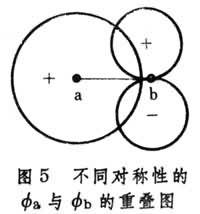 ③ 对称性条件:有时φa与φb虽然重叠,但B=0,例如当核间距Rab选作z轴(表1),φa=s,φb=py,这是因为s轨道相对xz平面为对称的,而py为反对称的。  将式(7)用于同核双原子分子,φa和φb可以是分属两原子的同一原子轨道,这时有:  (8)ψI对分子中心为对称,属于g;ψⅡ为反对称,属于u。其次,若φa=φb=s(或=pz),ψI和ψⅡ均对核间距(z轴)为轴对称,属于m=0的σ态;但对φa=φb=py(或px),则存在通过R的节面,属于m=±1的π态,细节列于表2中。 (8)ψI对分子中心为对称,属于g;ψⅡ为反对称,属于u。其次,若φa=φb=s(或=pz),ψI和ψⅡ均对核间距(z轴)为轴对称,属于m=0的σ态;但对φa=φb=py(或px),则存在通过R的节面,属于m=±1的π态,细节列于表2中。 分子轨道的能量 决定于组成原子轨道的类型和原子轨道间的重叠,例如σg1s和σu1s比σg2s低得多,这是由于原子轨道1s的能量比2s的低得多。同理,因为除氢原子外,2s能量显著低于2p的能量,故σg2s比σg2p能量低。另外,只要核间距不很小,两个2s轨道或两个2pz轨道之间的重叠比两个2py或2px之间的重叠大得多,因此成键和反键π轨道间的能量差比对应的σ轨道的差小。根据这种论述,表2中所列分子轨道次序可预料为: σg1s<σu1s<σg2s<σu2s<σg2p <πu2p<πg2p<σu2p (9)上式是一种最粗糙的轨道近似,更好的近似是包含更多的原子轨道,这些原子轨道符合有效成键作用的三条件。例如,代替单纯的2s以及2pz的LCAO所形成的σ型分子轨道应为:  (10)c1、c2、c3、c4确定后的四个σ轨道比原来的σg2s、σu2s、σg2p和σu2p更接近实际,其中σg2s、σu2s将降低,σg2p及σu2p则升高。加上当核间距变小时,πu2p要降低,导致式(9)中,σg2p与πu2p次序的可能颠倒: (10)c1、c2、c3、c4确定后的四个σ轨道比原来的σg2s、σu2s、σg2p和σu2p更接近实际,其中σg2s、σu2s将降低,σg2p及σu2p则升高。加上当核间距变小时,πu2p要降低,导致式(9)中,σg2p与πu2p次序的可能颠倒:πu2p<σg2p (11)N2分子就属于这一类型。 有了式(9)与(10)的能级次序,就可按能量最低原理和泡利原理来预言同核双原子分子的基态(表3)。  表中的符号Σ、Π、… 意义与σ、π、… 相同,具有沿核间距方向角动量的含义,标志完整分子的态,由各个单电子轨道确定;右上角的+、-号指对平分两核的镜面反映为对称或反对称而言。 多原子分子的分子轨道 以上基于单电子波动方程近似解的轨道概念和方法,可自然地向复杂的多原子分子推广。对双原子分子,存在沿核间距方向的角动量量子数 m=0,±1,…等来表征轨道或态;但对多原子分子,找不到象H娚那样简单而典型的分子,不能精确求解,给问题的讨论造成了麻烦。但由于弄清了量子数所表征的分子轨道对称性本质来源于分子自身的对称性,因而对称性分析(群论)会给出任何分子电子状态的重要信息,而无需知道分子轨道的具体函数。这方面的进展是巨大的,例如群论在化学中的应用,能级相关图、分子轨道对称守恒原理等的评述。此外,建立在单电子能级和轨道近似基础上的理论计算方法已发展起来,如自由电子分子轨道法、休克尔分子轨道法及推广的休克尔分子轨道法等。 如前所述,分子轨道和能级是单电子波动方程的本征解,即满足: Hψi=εψi (12)式中H是单电子哈密顿算符,其中的位能描写一个电子在固定分子骨架及其余电子的平均作用。因而,H与其余电子的运动状态,即轨道有关。前面的讨论丝毫未触及H的具体形式,也未对分子轨道作过严格定义,所得结论是定性地适用的。为适应理论的定量化发展,已经推导出著名的哈特里-福克方程(见自洽场分子轨道法),对于闭壳层电子体系,式(12)中的H采取福克算符的形式: 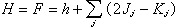 (13)式中h是纯核场中单个电子的哈密顿算符,2Jj-Kj=Ji和2Jj(j≠i)代表其余电子的平均静电势,Kj(j≠i)称交换势能,它来源于泡利不相容原理导致自旋相同电子间的相关作用。Jj和Kj的表示式均明显地与分子轨道有关,例如: (13)式中h是纯核场中单个电子的哈密顿算符,2Jj-Kj=Ji和2Jj(j≠i)代表其余电子的平均静电势,Kj(j≠i)称交换势能,它来源于泡利不相容原理导致自旋相同电子间的相关作用。Jj和Kj的表示式均明显地与分子轨道有关,例如: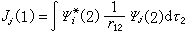 (14)式中(1)代表所考虑的单电子的坐标;(2)为另一电子,其分子轨道为ψj(2);r12代表两电子间距离。因此,式(12)的求解需事先设想一组ψj,按式(13) 求出H,然后得到一组新的ψj,重复这种步骤,直到最后一次循环中, 试探的ψj与解出的ψj接近和相同为止,称为自洽。 (14)式中(1)代表所考虑的单电子的坐标;(2)为另一电子,其分子轨道为ψj(2);r12代表两电子间距离。因此,式(12)的求解需事先设想一组ψj,按式(13) 求出H,然后得到一组新的ψj,重复这种步骤,直到最后一次循环中, 试探的ψj与解出的ψj接近和相同为止,称为自洽。采用LCAO方法,分子轨道ψk 按式(3)表示成原子轨道φl(l=1,2,…,n)的线性组合:  (15)代入(12)式,左右两端乘以φ奰并积分,得到一组ckl的方程组: (15)代入(12)式,左右两端乘以φ奰并积分,得到一组ckl的方程组: (16)式中 (16)式中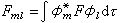 ; ;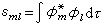 。求解归结为久期方程的本征值 Ek和本征向量 。求解归结为久期方程的本征值 Ek和本征向量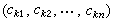 的自洽计算: 的自洽计算: 哈特里-福克方程虽然较仔细地考虑了电子间的排斥作用,但由于平均势场模型仍然使一部分固有的“相关作用”未予考虑,因而理论计算结果仍未达到定量符合实验值的精度。改进的途径是考虑组态相互作用,已经出现了多种组态相互作用分子轨道从头计算程序,用于量子化学研究。 参考书目 R.Dandel, G.Leroy, D.Peters and M.Sana,QuantumChemistry,John Wiley & Sons, New York, 1983. |
|
| 随便看 |
百科全书收录78206条中英文百科知识,基本涵盖了大多数领域的百科知识,是一部内容开放、自由的电子版百科全书。
Copyright © 2004-2023 Newdu.com All Rights Reserved
更新时间:2025/9/8 13:53:11
更新时间:2025/9/8 13:53:11