群上调和分析(卷名：数学)
harmonic analysis on groups
又称群上傅里叶分析、抽象调和分析。它是古典调和分析(即傅里叶级数与傅里叶积分理论)的统一与推广。它的研究对象是拓扑群上的函数或测度以及由它们构成的空间或代数。
概论 在古典调和分析中，为了研究一个实变量的函数（即实轴群R上的函数）或周期函数（即圆周群T上的函数），傅里叶提倡的方法是将此函数ƒ按三角函数系
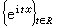或
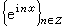展开。这就要先求出ƒ的傅里叶变换弮(t)，t∈R 或傅里叶系数
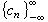，式中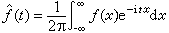
，
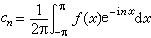， (1)然后用下述积分或级数还原出ƒ，
。 (2)这个方法就称为傅里叶分析方法，它的实质是通过对傅里叶变换进行讨论以达到对函数自身的了解。古典调和分析的两个方面(即级数部分与积分部分)无论就结果与方法而言都十分相似。此外，还发现沃尔什级数与傅里叶级数相似，梅林变换与傅里叶变换相似。这些相似使人们容易想到它们之间或许存在某种本质上相同的东西。把式(1)中两式合并写成
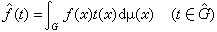， (1)′式中G分别表示R与T，弿分别表示R与Z（整数群），t(x)分别表示
，dμ(x)两种情况下都表示勒贝格测度dx。可以发现两种情况下G都是群;弿是由G决定的另一个群；t(x)是复值函数，它的值域在复平面的单位圆周上，并且满足乘性关系:t(x·y)=t(x)t(y)（式中·表示群的运算）；而dμ(x)是群G上一个有特殊地位的测度。除了傅里叶系数与变换可以这样统一以外，沃尔什系数与梅林变换也能用上述式 (1)′表示。对前者只需令G＝[0，1]，并在G中定义一个按位模2加法使之成为二进群D；弿＝Z+；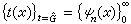
(式中{ψn(x)}是沃尔什函数系，按佩利次序排列);dμ就是勒贝格测度。对后者只需令G＝R+（正实数的乘法群）；弿＝R；
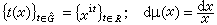。不仅如此，这样用群论观点看待沃尔什级数与梅林变换还给他们的研究带来了极大的方便。这些事实使人自然想到，调和分析的合适对象可以是更一般群上的函数。这正是群上调和分析这一学科诞生的动力。要在群上运用傅里叶分析方法，首先就要能在群上定义傅里叶变换。由式(1)′可知，这至少要求在如下三个问题中作奠基工作：①拓扑群上如何定义积分，特别是有没有一个测度能起到古典情形下勒贝格测度那样的特殊作用？②对给定的G，合适的弿是什么？③对给定的G能不能找出合适的"积木结构"
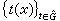(式(2)说明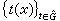能复合出许多函数，象积木能复合出许多建筑物一样)？20世纪20年代中期，（C.H.）H.外尔先对某些特殊紧李群，然后与F.彼得合作对一般紧李群得到了上述几个问题的满意回答，建立了著名的外尔-彼得定理，从而奠定了紧群上调和分析的基础。其后不久，A.哈尔对满足某些条件的局部紧群证明了第一个问题中的特殊测度（通称哈尔测度）的存在性。A.韦伊在其后的几年，对局部紧群上的哈尔测度及局部紧交换群上的调和分析进行了一系列的奠基研究，并于1940年发表名著《拓扑群上的积分及其应用》，从而宣告了这一学科的诞生。除此以外以И.М.盖尔范德为首的苏联学派对群上调和分析的形成与发展也作了十分关键的贡献。由于对既不是交换也不是紧的一般拓扑群，上述第二、三两个问题甚至都不能说已经有了令人满意的答案，因此这方面的调和分析仍处于待发展阶段。但若对群附加别的限制条件，如李群结构，则此时的 弿与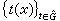有比较满意的选择，并且在某些特殊情形下，它们还能被具体地写出来。这样，古典调和分析中的某些定量结果也能推广到这种情形。群论观点进入调和分析除了有上述统一与推广的意义外，还使某些看起来彼此不相关的现象间的内在联系被揭示得更清楚，这使得调和分析内部各分支之间以及调和分析与其他学科例如泛函分析、代数学、群表示论、模形式等的联系变得更为密切。因此，群上调和分析可以说是一门既具应用价值（正如它对概率论、数论与微分方程等所起的作用所说明的）又具理论意义的综合性学科。
局部紧T2群 一个既有群结构（其群运算用乘法表示）又有拓扑结构，并且两者有某种联系的集合称为一个拓扑群。当它的拓扑结构是局部紧的并且满足T2分离性时就称为局部紧T2群。群上调和分析主要只考虑这样的群。
哈尔测度 局部紧群 G上的在左(右)平移作用下不变的非负(不恒为0)正规波莱尔测度称为G的左(右)哈尔测度。所谓“平移作用下的不变测度”的含意可以有两种等价理解。设μ是G上一个测度。对每个α∈G都可定义G上的一个左平移x→αx，凬x∈G，相应地每个μ可测集E被平移为αE。如果所有αE都是μ可测的，且αE与E的μ测度相等，则称μ是左平移不变的。另一种理解基于测度的下述等价定义，即测度μ是K(G)（G上所有有紧支集的连续函数的全体）上的线性泛函，或称K(G)上的积分，记为
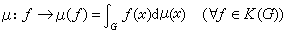。 (3)对每个α∈G可以定义作用在K(G)上的左平移算子
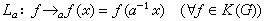。如果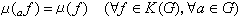
， (4)那么，μ称为左平移不变的。哈尔测度对怎样的G是存在且惟一的，这是一个困惑人们多年的难题。早在19世纪末与20世纪初，许多数学家就对一些具体的群探讨过这个问题。直到1933年，哈尔才在这个问题上迈出决定性的一步。他对任意有可列开基的局部紧群确立了哈尔测度的存在性。韦伊随后用式(3)理解测度，从而对哈尔的结果作了整理与推广，他对任意局部紧群确立了哈尔测度的存在性与（除一个常数倍数以外的）惟一性。此外，角谷静夫与H.嘉当也在这个问题上作出过很重要的贡献。
在交换群情形，左、右哈尔测度是一样的，但在非交换情形却不一样了，它们由哈尔模函数相互联系。任取一个左哈尔测度dx，则对任意
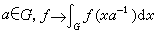仍是K(G)上的一个左不变积分，故由惟一性知存在正数Δ(α)，使
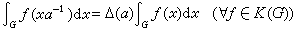。 (5)这个Δ(α)是G 到正数乘法群R+内的一个连续同态，它称为G的哈尔模函数。Δ(α)=1 的群称为幺模群。除交换群外，所有紧群都是幺模群。对任意取定的左哈尔测度dx，通常的变量代换引出的两个常见测度可通过模函数如下表示
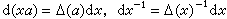。这里dx-1可以证明是一个右哈尔测度。当考虑G 模某个子群(或正规子群)H 所得的齐性空间（或商群）G/H 时，其上的拟不变（或不变）测度可通过韦伊公式互相联系，因此群上调和分析可服务于齐性空间上的调和分析。
对偶群、对偶对象 它是拓扑群的某种意义下的对偶，可以用来研究拓扑群的结构，也可以用来定义傅里叶变换。
设G是交换的局部紧T2群，G到群T内的连续同态称为一个（连续）特征。譬如群R与T的所有（连续）特征分别为
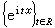与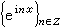
。设弿是G 的所有（连续）特征的集合，可以定义 弿中的乘法为
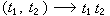，其中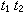
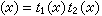，右边是复数的普通乘法。还可以定义它的拓扑如下，对于所有ε>0与紧集K，令
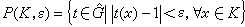为弿的单位的基本邻域组。可证，弿在这样定义的群与拓扑结构下是一局部紧T2交换群，它就称为G的对偶群。可以证明在这样定义的对偶群概念下，
，
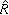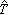分别与R及Z拓扑同构。对非交换的局部紧T2群G，定义弿是G的所有连续不可约酉表示的等价类的全体，它在适当的拓扑下便称为G的对偶对象。如G是紧群，则G的每个连续不可约酉表示U都是有限维的，即存在希尔伯特空间HU，dU=dimHU＜∞，使得U(x)对每个x∈G都是HU上的酉算子。此时弿的合适拓扑是离散拓扑。
关于这个对偶概念，有一个重要的事实是对偶定理。对交换群的庞特里亚金-范坎珀定理说，在如下的自然嵌入映射α下，
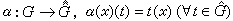，G与彁拓扑同构。这个定理说明，由弿可以决定G，并且G与弿的地位是平等的。对于非交换的紧群G，也有一个类似的田中-克雷恩对偶定理。它说，弿也惟一地决定了G，即可通过弿 构造一个紧群与G拓扑同构。群代数、测度代数、傅里叶代数、傅里叶－斯蒂尔 杰斯代数 这些是群上调和分析最主要的研究对象。考虑一般局部紧 T2群G。L1(G)是G上（左）哈尔可积函数的等价类的全体，在普通线性运算，范数
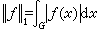，卷积乘法*
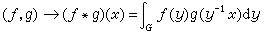，以及对合运算～
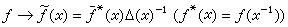下所成的巴拿赫对合代数。它，或者它的单位扩充，常称为群G的群代数。M(G)是G上所有复值正规有界波莱尔测度的全体在普通线性运算、全变差范数
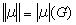、卷积乘法*
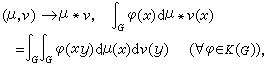以及对合运算～
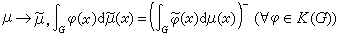，下所成的巴拿赫对合代数，它就称为G的测度代数。傅里叶代数A(G)与傅里叶－斯蒂尔杰斯代数B(G)在交换群时不是新概念。它们是
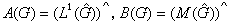，式中括弧外面的∧表示傅里叶变换。当G非交换时，它们却是新概念。 B(G)定义为G上所有连续正定函数的集合p(G)线性生成的空间，在普通线性与乘法运算与适当拓扑下所成的一个巴拿赫代数。A(G)定义为B(G)∩K(G)在B(G)内的闭包。A(G)有一个非常著名的特例就是群T上所有绝对收敛的傅里叶级数所构成的代数A(T)即(L1(Z))┇。关于它，有一个著名的维纳-莱维定理。对一般的A(G)与B(G)有一些类似的事实。傅里叶变换、傅里叶－斯蒂尔杰斯变换 设G是交换群，弿是它的对偶群，定义
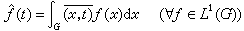， (6)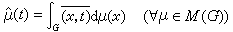
， (6)′式中(x，t)是t(x)的对称写法，“─”表示复数共轭。它们称为 ƒ与μ的傅里叶变换，后者有时也称为傅里叶-斯蒂尔杰斯变换。当G非交换时，下面以紧群为例，设σ∈弿是任一表示等价类， 
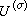是任取的属于σ的一个表示，记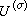的表示空间为Hσ，其维数为dσ，
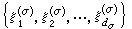是任取的一组标准正交基，〈·，·〉表内积，记D是Hσ内如下定义的共轭线性算子：
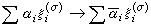，则
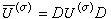称为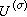
的共轭表示。则可以定义傅里叶变换为
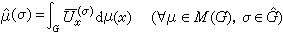。 (7)这是一个算子值积分，它的意义是凬ξ，η∈Hσ有
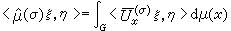。这个定义中虽然有某些不确定的因素（如
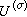与D 的选取），但傅里叶变换的本质性质并不因此受影响。傅里叶变换有如下最基本事实（仅以交换群为例）。①μ→▇是M(G)到B(弿)上的，以及ƒ→弮是L1(G)到A(弿)上的巴拿赫对合代数同构，并且B(弿)中的元素都是一致连续的函数，A(弿)中的元素是无穷远处趋于0的连续函数。后者称为黎曼-勒贝格引理。此外“同构”蕴涵变换是一一的，即▇呏0推出μ呏0。这是傅里叶变换的惟一性定理。②对每个t∈弿，μ→▇(t)与ƒ→弮(t)分别是代数M(G)与L1(G)的复同态，特别有
。傅里叶变换与卷积的这个关系是傅里叶变换的重要性的主要来源。也有用交换巴拿赫代数的盖尔范德理论来定义交换群上的傅里叶变换的。即ƒ∈L1(G)的傅里叶变换定义为ƒ作为巴拿赫代数L1(G)的元素的盖尔范德变换。这种定义与前述定义是一致的。
普朗歇尔定理、 豪斯多夫－杨定理 普朗歇尔定理是交换群上调和分析中最重要而基本的定理，它说傅里叶变换F是L2(G)到L2(弿)上的一个等距同构算子。其确切叙述为：G 与弿 上的哈尔测度可以规范化， 使得原在L1(G)∩L2(G) 上定义的傅里叶变换F 可以扩充为整个L2(G)到L2(弿)上的一个等距同构(仍记为F)， 并且它的逆算子正好是定义在L2(弿)上的傅里叶逆变换F-1:g→媝，
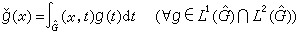。普朗歇尔等式的等价形式是下述帕舍伐尔关系
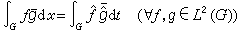(8)它也可写成对称形式
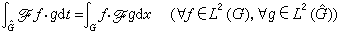。 (8)′将上述指标2推广到1≤p≤2，便得到豪斯多夫-杨定理：定义于
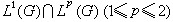上的F可以连续地扩充为整个Lp(G)到L悜(弿)内的有界算子，算子范数不大于1，其中p′是p的相伴数即满足
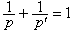。此时的帕舍伐尔关系为
，
，
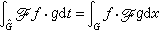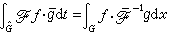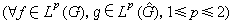式中第二式说明F，F-1互为共轭算子。既然F与F-1无本质差别，故对F可进行对偶讨论。外尔－彼得定理 这是紧群上调和分析中最重要而基本的定理，它相当于对交换群的普朗歇尔定理。设G是紧群，dx是使G的测度为1的哈尔测度，σ∈弿，
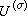是属于类σ中的一个不可约酉表示，Hσ是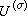的表示空间，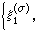
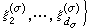是Hσ中一组标准正交基，函数
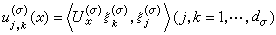，称为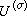
的表示函数。对于前面定义的
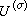，其表示函数即为
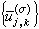。外尔-彼得定理 设G是紧群，则
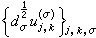构成了L2(G)的一个完备标准正交系，此即，
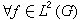有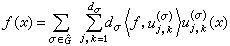
， (9)式中右边级数在L2(G)中收敛，以及〈·，·〉表L2(G)中的内积，
；并且帕舍伐尔关系成立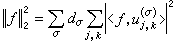
。 (10)式(9)，(10)可用傅里叶变换来表示。如只看式(9)，因为
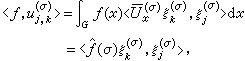故可得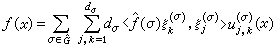
。 (9)′此外还可用傅里叶变换的迹来表示式(10)，因为
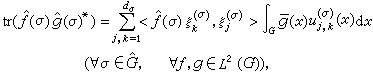故有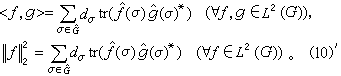
调和分析与群表示论 调和分析的最重要任务是把所在群G上的函数空间L2(G)进行直和(或连续型直和)分解，而这正是群G的一个非常重要的酉表示，即左正则表示
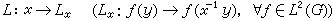的不可约分解。用这种观点看待古典调和分析虽然未免是小题大作，但对群上调和分析而言，这种观点却十分流行。以至有人认为调和分析就是用表示的分解来对函数空间进行分解的一种方法。以紧群为例来说明这种关系，符号沿用外尔-彼得定理中所述，记
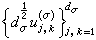与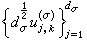
生成的线性空间分别为Tσ(G)与Tσ，k(G)，则因
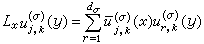，说明Tσ，k(G)是L的不变子空间。定义转换算子T为
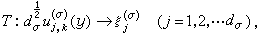则有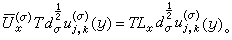
这说明L在Tσ，k(G)上的局限与
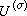等价。故外尔－彼得定理的断言 
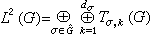正与L的不可约分解
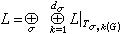对应。参考书目
E.Hewitt and K.R.Ross，Abstract harmonic Analysis，Vol.1～2，Springer-Verlag， Berlin， 1970.
Y.Katznelson，An Introduction to harmonic Analysis，Dover， New York， 1970.
W.Rudin，Fourier Analysis on Groups，Interscien-ce， New York， 1962.
G.Warner，harmonic Analysis on Semi-Simple Lie Groups，Vol， 1～2，Springer-Verlag， Berlin， 1972.