相关分析(卷名：社会学)
correlation analysis
描述两个或两个以上变量间关系密切程度的统计方法。变量间关系的密切程度常以一个数量性指标描述，这个指标称相关系数，是社会学中较为普遍采用的一种资料分析的方法。根据变量的层次和数目，相关分析可作如下的分类。
定距变量以上的相关 根据相关的准则，以直线为准，称作直线相关；以非直线为准，称作非直线相关。无论是直线相关或非直线相关，都可以进一步根据变量数目来分类。
简单直线相关 讨论两定距变量间线性相关的程度与方向。例如，父辈受教育年限与子辈受教育年限之间的关系。简单直线相关系数r，又称皮尔逊相关系数或积矩相关系数。
式中x、y为两相关变量，它们的测量值都是成对的：(x1，y1)，(x2，y2)，……，(xn，yn)。相关系数r 的性质有：①相关系数的取值范围为-1≤r≤+1；②r为正值时，两变量间为正相关(图a)；
③r为负值时，两变量间为负相关(图b);
④相关系数的绝对值│r│愈大，两变量间相关程度愈密切。r＝+1，为完全正相关（图c）；
r＝-1，为完全负相关(图d)；
r＝0，两变量完全无关(图e)。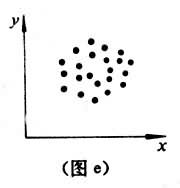
复相关 研究一个变量 x0与另一组变量 (x1，x2，…，xn)之间的相关程度。例如，职业声望同时受到一系列因素（收入、文化、权力……）的影响，那么这一系列因素的总和与职业声望之间的关系，就是复相关。复相关系数R0.12…n的测定，可先求出 x0对一组变量x1，x2，…，xn的回归直线，再计算x0与用回归直线估计值憫之间的简单直线回归。复相关系数为
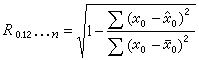R0.12…n的取值范围为0≤R0.12…n≤1。复相关系数值愈大，变量间的关系愈密切。偏相关 研究在多变量的情况下，当控制其他变量影响后，两个变量间的直线相关程度。又称净相关或部分相关。例如，偏相关系数 r13.2表示控制变量x2的影响之后，变量 x1和变量x3之间的直线相关。偏相关系数较简单直线相关系数更能真实反映两变量间的联系。
偏相关系数、复相关系数、简单直线相关系数之间存在着一定的关系。以3个变量x1，x2，x3为例，它们有如下的关系：
或
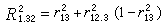
定序变量的相关 讨论两个定序变量间的相关的程度与方向。又称等级相关。例如，研究夫妇双方文化程度的相关等。等级相关系数有R系数和γ系数。
R系数 计算方法与简单直线相关系数相同。
式中X，Y分别为x，y的测量值的等级。英国统计学家 C.E.斯皮尔曼从R系数中推导出简捷式，称斯皮尔曼等级相关系数：
式中di=xi-yi，i=1，2，…，N（N为次数）。等级相关系数 R具有与简单直线相关相同的性质：取值范围在〔-1，+1〕之间；R的绝对值愈大，变量间的等级相关程度愈大。
γ系数 适用于资料次数N 很大的情况。
式中Ns为同序对数目，Nd为异序对数目。同序对表示两个个案(xi，yi)和(xj，yj)相比时，具有xi＞xj，则yi＞yj的性质;反之，若xi＞xj，但yi＜yj，则称作一个异序对。
γ系数的取值范围在〔-1，+1〕之间。γ的绝对值愈大，变量间的等级相关程度愈大。
定类变量的相关 研究两个定类变量间的相关程度。又称品质相关。例如，性别与宗教信仰，民族与宗教信仰等。为了研究定类变量间的相关，先将资料按两种变量进行交叉分类，设x共分c类，y共分r类，得r×c频次分配表。
列联表中变量相关程度有两种测量方法：λ系数和τ系数。
当边缘分布与每列的分布（即条件分布）相同时，λ和τ达极小值：λ=0，τ=0，表示x与y无关。当各行及各列都只有一个不为零的频次值时，λ和τ达极大值:λ=1;τ=1，表示x与y全相关。
如果列联表中所分类别都只有两类：c=2；r=2。称2×2列联表。它的相关系数可按φ系数和Q系数计算:
当φ=0或Q=0时，表示x变量与y变量无关。而当φ或Q的绝对值为1时，表示x变量与y变量全相关。
r×c列联表中变量的相关性，有时还采用列联系数。
式中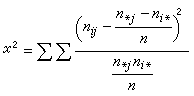
列联系数c取值范围在0≤c＜1。20世纪80年代以来，社会学中已很少使用c系数，一般用λ系数和τ系数。