泊松括号(卷名：力学)
Poisson bracket
法国科学家 S.-D.泊松求解哈密顿正则方程时所用的一种数学符号，它定义为：
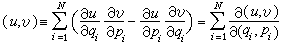，式中u和v是2N个正则变数qi，pi(i＝1，2，…，N)的两个任意函数。泊松括号经正则变换(q，p)→(Q，P)是不变的，即
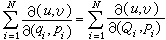。此外尚有以下特性：①(u，v)＝-(v，u)；
②(u，u)＝0；
③(u，c)＝0，c为常数；
④(u＋v，w)＝(u，w)＋(v，w)；
⑤(u，vw)＝(u，v)w＋(u，w)v；
⑥((u，v)，w)＋((v，w)，u)＋((w，u)，v)＝0；
⑦
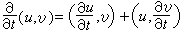；⑧正则方程可用泊松括号写作：
(qi，H)＝妜i，
(pi，H)＝妛i；
⑨任一函数u(q，p，t)的全微分可写作：
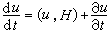；⑩正则方程的第一次积分u(q，p，t)＝c可写作：
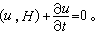
泊松括号在量子力学中用来表示两个算符的对易关系乘上
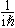（媡是普朗克常数，
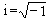）。 例如对算符弿和忓有：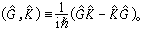
这样，量子力学中对力学量弲，上面⑨中的关系式依旧成立，即
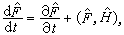式中彑是厄密算符。参考书目
周世勋编：《量子力学》，上海科学技术出版社，第四版，上海，1962。