泛代数(卷名：数学)
universal algebra
以一般代数系统为研究对象的一个数学分支。在诸如矩阵群、置换群、变换群等具体的群概念基础上，经过抽象概括而得出抽象群的概念；与此类似，可以在一般的群、环、布尔代数、模、格、半群等等概念之上再抽象，得出能概括它们的共性的更加一般的概念。这种方法和任务，早在1898年A.N.怀特海就已提出了，但是直到20世纪30年代末期在G.伯克霍夫的著名工作之后，泛代数才真正发展起来。
设A是一个非空集合，n≥1是自然数，所谓A的一个n元运算，是指A×A×……×A（n个A的笛卡儿积）到A的一个映射ω，元素(α1，α2，…，αn)在映射ω下的像α1α2…αnω，就是 α1，α2，…，αn在n元运算ω下得到的结果。规定A的一个零元运算就是在A中标定一个元素。
集合 A和其上若干个（有限或无限个）运算组成的运算集Ω一起，统称为一个代数系统或Ω代数（简称代数），记作〈A，Ω〉。简而言之，所谓代数系统，就是带运算的集合。如果代数系统〈A，Ω〉的运算集Ω与代数系统〈A′，Ω′〉的运算集Ω′之间有一个一一对应φ，且相对应的运算是相同元数的，那么<A，Ω>和〈A′，Ω′〉称为是同型的。常把同型代数的运算集Ω和Ω′按对应φ等同起来。例如，群可看成具有一个二元运算（乘法）、一个一元运算（取逆元）和一个零元运算（单位元）的代数系统；有单位元的环可看成具有两个二元运算（加法和乘法）、一个一元运算（取负元）和两个零元运算（零元和单位元）的代数系统；布尔代数可看成具有两个二元运算（交和并）、一个一元运算（取补元）和两个零元运算（0和1）的代数系统。有单位元的环和布尔代数，就可视为同型代数。然而，域不能看成代数系统，因为域中对乘法取逆元不是对域中每一元都有意义，而只是域上的一个“部分运算”。
泛代数首先把群论、环论和格论中一些共有的概念和平行的结果，推广到代数系统上来。例如，同构、同态、合同关系、子代数系统等基本概念，以及从已给的代数系统建立新的代数系统的各种构造方法：取子代数系统、取同态像、直积、亚直积、正向极限、反向极限、超滤积、自由代数等，它们和群论或环论中相应的概念十分类似。就其重要的介绍如下：
设〈A，Ω〉和〈A′，Ω′〉是两个同型代数（已将它们的运算集等同起来），如果φ是集A到集A′的一个映射，且对Ω中任意n 元运算ω 满足条件(C)：
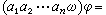
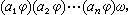凬αi∈A，那么φ 称为代数<A，Ω>到〈A′，Ω′〉的一个同态。当ω是零元运算时，条件(C)是指A中ω 所标定的元素在φ下的像，恰是A′中ω 所标定的元素。当φ为A和A′间的一一映射时，则说φ是这两个代数间的一个同构。设θ是集合A的一个等价关系。所谓θ是代数<A，Ω>的一个合同关系，意指对Ω中任意运算ω有:若αiθbi，则(α1α2…αnω)θ(b1b2…bnω)。用<A，Ω>的一个合同关系θ，很容易构造一个新的代数<凴，Ω>，其中凴是A中θ的等价类ā、α∈A的集合，凴的运算ω∈Ω定义为
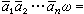
。由于θ是合同关系，故此定义确给出凴的一个运算。显然，〈A，Ω〉和〈凴，Ω〉是同型代数，而A到凴上的对应φ:α→ā是它们间的同态。用正规子群（或理想）可以刻画群（或环）的合同关系，但是这对Ω代数已不可能了，例如半群的合同关系已不能用子半群去刻画。然而，对于泛代数仍有和群论类似的关于同态的基本定理以及第一、第二同构定理。
和群（环）论类似，在泛代数中也讨论代数的子代数格、合同关系格、代数的自同构群等问题。
任取非空集M 和集
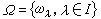。每一ωλ 对应一个非负整数nλ，并把ωλ称为nλ元运算符号。nλ=0的ωλ的全体，记作Ω0。令N =M ∪Ω0，用归纳法定义阶为非负整数n的字，规定N 中元素是阶为0的字。设阶为m(m<n)的字已定义，规定阶为n的字是一切形如(α1，α2，…，αk，ω)的符号，其中ω ∈Ω是k元运算符号，k≥1;而αi是阶为mi的字，且
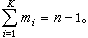令F表示所有字组成的集合，并在F中规定nλ元运算
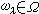为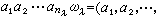
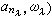。于是就得到一个Ω代数〈F，Ω〉，并称之为自由Ω代数，特记作F(Ω，M )。它具有自由群所具有的那种泛性质(见无限群)。特别，任一Ω代数总可以看作某个自由Ω代数的同态像。本原类是泛代数中的一个重要概念，可以用自由代数来定义。取自由代数F =F(Ω，X)，其中可数集X={x1，x2，…}。取字对
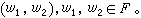所谓与F同型的代数<A，Ω>满足恒等式w1=w2，是指对F 到<A，Ω>的任意同态φ都有
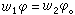这等于说用Ω代数A中任意元素αi去代替字w1、w2中的xi后所得到的A中元素彼此相等。取
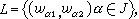它是F中字对的集合。满足所有恒等式
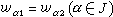的Ω代数的全体，称为一个本原代数类。例如，群的全体，结合环的全体，域K上李代数的全体，格的全体等都是本原代数类。可以证明，每一本原类都有“自己的自由代数”，它在这个本原类中具有自由群在群类中所具有的那种泛性质。泛代数的一个特有结果是重要的伯克霍夫定理：一个Ω代数类W是一个本原类，当且仅当W 中任意代数的子代数、同态像以及它们的直积也都在W 中。它是泛代数作为独立分支发展的起点。在泛代数中还讨论在给定的本原类中判定两个字是否相等的所谓字的问题，本原类中自由代数的基的问题等。
泛代数一词，通常包含Ω代数与结构这两方面的内容，它们之间有其相通之处，然而，就其研究方法和所讨论的问题来说，是有很大区别的。Ω代数是其上定义一些n元运算的集合，用通常的代数方法去研究，就组成了上述的“狭义”泛代数的内容。结构是其上定义有一些n元关系（其特例是n元运算）的集合，用数理逻辑方法（使用一阶谓词演算的语言）去研究，就组成了模型论的内容。泛代数的方法在自动机理论和程序语言的语义学中已有应用。
参考书目
P.M.Cohn，Universal Algebra， Harper and Row，NewYork，1965.
G.Grtzer， Universal Algebra，2nd ed.，Springer-Verlag，New York，1979.