原子的量子理论(卷名：物理学)
quantum theory of atom
以量子力学为基础的关于原子结构的理论。N.玻尔关于原子结构的理论（见玻尔氢原子理论是原子的量子理论的先驱，它的建立推动了原子结构的研究。研究的深入又揭示了玻尔理论与实验结果间的一系列矛盾。而解决这些矛盾则导致量子力学的诞生。
氢原子是最简单的原子，只有一个电子绕质子运动。用量子力学处理氢原子得到的结果精确度最高，处理多电子原子问题困难则大得多，但氢原子理论中的一些结果对认识多电子原子的运动很有帮助。下面介绍氢原子的量子力学理论的概要，再略述多电子原子的量子力学理论。
氢原子 氢原子核的质量约为电子质量的1836倍，故可把运动简化为电子在静止的原子核的库仑场中运动，以r代表电子到核的距离，-e代表电子的电荷，则电子的位能为
。根据量子力学的理论，电子的运动状态用一波函数 Ψ来描写。波函数 Ψ是电子坐标 r的函数。
表示电子在空间各点出现的几率密度。当电子与氢原子核组成原子时，电子受库仑力的作用被束缚在核附近一小区域内。与此相应，几率密度将只在核附近的一个小区域内不等于零，这种状态叫束缚态。要确定束缚态波函数，需要解定态薛定谔方程
(1)式中彑为哈密顿算符，又称能量算符。彑的表示式为
。 (2)式中媡＝h/2π，h为普朗克常数，me为电子质量。 在式(1)中，E 为能量本征值(见本征函数和本征值)，在束缚态时能量E取分立值，其表示式为
， (3)此即玻尔公式。n决定能级值，称为主量子数。与此同时可决定对应于能级En的波函数。当电子在库仑场中运动时，能量与轨道角动量都是守恒量。用量子力学的语言，即电子的能量E、轨道角动量z分量Lz（有时用
表示）与
可以同时有确定值。此时波函数ψ除需满足式(1)还应同时满足本征方程
(4)
(5)在球坐标(r，θ，嗞)系中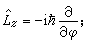
(6)
(7)解式(4)可得L2的值为
(8)Л叫角量子数，也称轨道角动量量子数。由于Л取分立值，故L2也取分立值。这就是所谓轨道角动量量子化。式(8)比玻尔所提出的公式更确切。解式(5)得Lz的值为
， (9)
。 (10)式中ml叫磁量子数，式(9)、(10)表明Lz也是量子化的，并且│Lz│永远小于或等于L。当电子波函数ψ同时满足式(1)、(4)、(5)时，它描写电子的E、L2、Lz同时有确定值的状态。此时波函数用r、θ、嗞作为变量，并用量子数n、Л、ml作为标记。则有
(11)式中
是球谐函数，Rnl(r)叫做径向波函数。
即表示电子能量等于
的状态。 式(10)表明磁量子数ml受角量子数l的限制。角量子数Л则受主量子数n的限制，关系是
Л＝n-1，n-2，…，1，0。 (12)由n、l、ml间的关系可见，对应于一个能级En有n2个独立的波函数
，它们分别描写不同角动量的态。
在图1中画出了n=1、2、3时径向几率密度，其定义为
。由图可见，几率密度具有束缚态的特征。图中虚线表示
与r的关系，实线表示
与r的关系。
给出了氢原子中电子在各点出现的几率。图2给出了n、Л、ml不同时电子的几率分布。在l=0时，几率分布是球对称的。在l厵0时，几率分布对于z轴是对称的。图2中，z轴是垂直的，并通过几率分布的对称中心（即原子核）。考虑到电子具有自旋以后，波函数还须扩充到能描写电子自旋状态。已知自旋角动量的 z分量sr（有时用pms表示）也是量子化的，即
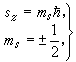(13)常称ms为自旋磁量子数。常用记号α与β分别代表
与
的状态。于是包括自旋状态的波函数用四个量子数n、l、ml、ms作为标记，则波函数为
(14)可以把轨道角动量与自旋合成总角动量，在封闭系统中总角动量是守恒量。以J（有时用pj）表示总角动量，则有
(15)j 叫做总角动量量子数。j 的值决定于角量子数Л与自旋量子数，其规律为
(16)总角动量的z分量Jz（有时用pmj表示）也是量子化的 
。 (17)量子数mj只能取分立值，并受j 值的限制
。 (18)引入总角动量以后，电子的状态用量子数n、l、j、mj表示。对应的波函数为
， 它的数学表示式与
不同的。在不考虑自旋轨道耦合时，
与
都代表相同的能量状态。在考虑了自旋轨道耦合以后，电子状态用
描写更为确切。由于电子在氢原子中运动速度v与光速с的比值约为10-3的数量级。 比较精细的理论必须考虑电子质量随速度改变的相对论效应。P.A.M.狄喇克提出了一个考虑了电子自旋的相对论运动方程。在狄喇克的理论中，波函数具有四分量。写成数学形式，即
(19)此时哈密顿算符彑也包含4×4的矩阵。根据狄喇克理论，氢原子能级公式为
(20)式中n为主量子数，
α为精细结构常数，它的表示式与数值为 
。 (21)由于α2为10-4数量级，故可把式(20)按α2的级数展开。把式(20)展开到α4项，得到
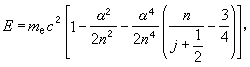(22)式中第一项表示电子的静止能量，这是相对论理论所特有的。第二项即玻尔能级公式，第三项代表自旋轨道耦合与质量随速度改变的影响。根据狄喇克理论，电子状态仍可用量子数n与j描述，能级值也决定于量子数n与j，这样，当两个状态具有相同n与j但l不同时，能量应该相同。例如，2s2S½与2p2P½能级应该相同。1947年W.E.兰姆与R.C.雷瑟福发现此二能级有微小差异，人们称此差异为兰姆移位。应用量子电动力学的理论可以解释。
多电子原子 从氦元素开始，原子至少有二个电子，属于多电子原子。如果原子序数为Z，则有Z个电子。即使不考虑原子核的运动，仍应考虑Z个电子的运动，因一个电子的运动要用三个空间坐标(x，y，z)与一个自旋坐标sr描写，Z个电子的运动就要用4Z个坐标描写。引入缩写
(23)代表第 i个电子的坐标，则原子的波函数Ψ 可表示成
(24)根据量子力学理论，系统的能量E、总角动量量子数J与宇称可以同时有确定值。但是能量E须由定态薛定谔方程
(25)决定，同时解得波函数Ψ。多电子原子的哈密顿算符要比氢原子的复杂得多。哈密顿算符彑主要包括每个电子的动能算符，每个电子在原子核场中的位能，以及电子间的相互作用。正是电子间的相互作用使问题复杂化。这时，每一电子的运动受到其他电子运动的影响，这使式(25)不存在严格的解。
在处理多电子问题时，常引入一合理的物理模型，即独立粒子模型。在此中假设每一电子运动仍可用单粒子波函数
来描写。这里
表示第 i个电子在原子核以及其他电子场中运动的波函数。考虑到每一电子在核周围迅速运动，电子场可以用平均场代替，这平均场又可用一中心场来近似表示。于是问题简化为研究每一电子在中心场中的运动。当电子在中心场中运动时，如同氢原子一样，电子的能量、轨道角动量与自旋可以同时有确定值。电子状态仍然可以用量子数n、l、ml、ms表示。单电子波函数仍可记作
。它的具体数学表示式则不同于氢原子的波函数。在考虑了自旋轨道耦合以后，电子状态也可以用量子数n、l、j、mj表示。总之在独立粒子模型中，每一电子状态可用四个量子数以及相应波函数表示。计算得单电子波函数以后，可以得到系统的波函数。最初在D.R.哈特里提出的理论中
， (26)为了保证不违背泡利不相容原理，他要求任意两个电子的四个量子数不相等。以后J.C.斯莱特指出，更确切的做法是用反对称化的波函数，即
(27)得到系统波函数以后，原子的能级可以通过式
(28)获得。这个式子表示哈密顿算符对波函数Ψ 的平均值。同时每一电子的角量子数li也决定了原子的角量子数J值和原子的宇称。多电子原子的核心问题是求出单电子波函数
。根据物理模型，每一电子是在其他电子平均场中运动，而平均场又要通过单电子波函数来计算。这种方法叫量子力学的自洽场近似法。自洽场法中要求解一组微分积分方程以得到单电子波函数。哈特里最初从式(26)出发建立了一组方程，叫哈特里方程。以后B.A.福克考虑到正确的波函数应该用式（27）表示，得到了更精确的方程，叫哈特里—福克方程。求单电子波函数的另一种方法是用量子力学的变分法。此法在研究轻元素时用得更多些。无论哪一种方法都必须进行数值计算。计算工作量很大，要用大型电子计算机。参考书目
周世勋编：《量子力学教程》，人民教育出版社，北京，1979。
G.Herzberg，Atomic Spectra and Atomic Structure，Dover，New York，1944.
J.C.Slater， Quantum Theory of Atomic Structure，Vol.1，2，McGraw-Hill，New York，1960.