双不动中心问题(卷名：天文学)
two fixed-center problem
一种特殊的限制性三体问题。在这个三体系统中，两个主天体(或称有限质量天体)固定不动，第三个小天体在两个固定的主天体吸引下运动。欧拉、拉格朗日、勒让德、雅可比等人很早就研究过这个问题。双不动中心问题是限制性三体问题中少有的可积情况之一，其解包含椭圆积分，比二体问题复杂些。双不动中心实际上是不存在的。但是，只要一个主天体绕另一个主天体的运动速度比小天体的运动速度小得多时，就可略去由此引起的惯性力，近似地作为双不动中心问题，对应的解至少可作为小天体运动的第一近似，即中间轨道。这在研究人造地球卫星运动理论中是有用处的。
人造卫星(即小天体)绕旋转对称的地球运动时，地球自转对卫星运动没有影响。因此，可以将地球看成是由压缩了的很多分散的“不动体”集合而成的，进而简化为两个质量相等的不动体的结合，这两个不动体的总质量等于地球质量。这样，就把一个复杂的问题简化成双不动中心问题。相应的卫星运动方程为：
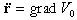，式中V0为双不动中心构成的引力场位函数。阿克肖诺夫为了使V0尽量接近于真实的地球引力场位函数V，取V0为：
，
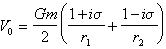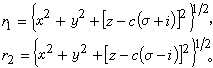式中G是引力常数；m是地球质量；r1，r2分别是小天体到双不动中心的距离，
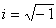。这相当于构成地球的两个不动体对称地分布在z轴上，但它们的质量和相互距离用共轭复数形式表示。适当选取两个待定常数c 和σ，可以使V0包含V的球谐展开式的主要带谐项 J2、J3和J4中的大部分。利用空间蒂勒变换，将x、y、z 转换为ξ、η、λ：x=c[(1＋ξ2(1－η2))1/2cosλ ，
y=c[(1＋ξ2(1－η2))1/2sinλ ，
z=cσ+cξη， 可将人造卫星的运动方程转化为对于ξ、η、λ的可积形式。它的解虽然包含椭圆积分，但用来作为中间轨道要比椭圆轨道精确得多，它包含了地球形状摄动的主要部分。文蒂的中间轨道就是这种近似处理的特例(σ =0)。
要在上述中间轨道基础上进一步求出人造地球卫星运动更精确的解，就得求摄动，相应的摄动函数为R=V-V0。解决这个问题仍然是比较麻烦的。因此，即使在人造卫星绕地球运动这个特定的问题中，引用双不动中心的模型，也不能完全解决问题。