流体动力学(卷名：力学)
fluid dynamics
流体力学的一个分支，研究作为连续介质的流体在力作用下的运动规律及其与边界的相互作用。广义地说，研究内容还包括流体和其他运动形态的相互作用。流体动力学与流体静力学的差别在于前者研究运动中的流体；流体动力学与流体运动学的差别在于前者考虑作用在流体上的力。流体动力学包括液体动力学和气体动力学两大部分。它的研究方法也和流体力学一样有理论、计算和实验三种。三种方法取长补短，相互促进。
流体动力学的研究主要包含下述内容：
应力张量 A面上的面力分布密度
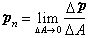称为应力，其中Δ
为面积元ΔA的法线单位矢量n所指向的流体或固体作用在ΔA上的面力。过任一点Μ可以作无数个不同方向的表面，作用在这些不同表面上的面力一般说来是互不相等的，因此要描写一点的应力需要知道所有通过Μ点的面上所受的应力。但是，过同一点不同面上所受的应力并不是互不相关的。事实上，只要知道三个相互垂直坐标面上的应力x、y、z，则利用作用在体积元上的面力平衡的事实可以证明，任一以n为法线方向的表面上的应力都可按照下式通过x、y、z和n在直角坐标系中的投影α、β、γ表示出来：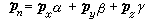
。因此，三个矢量
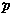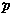x、y、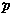z或九个量pij(i，j＝1，2，3)的组合可完全地描写一点的应力状况。pij组成的二阶张量称为应力张量。利用作用在体积元表面上的合面力矩等于零的事实可证明应力张量是对称的，即
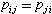。根据无粘性流体对于剪切变形没有抗拒能力和静止流体不能承受剪应力的事实可以断言：在无粘性流体或静止流体中，剪应力为零，而正应力(即法向应力)pxx=pyy＝pzz＝-p。p称为无粘性流体或静止流体的压力函数，它表征无粘性流体或静止流体在任一点的应力状态。
应力张量和变形速率张量的关系 牛顿的粘性定律
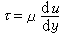只适用于剪切流动（见牛顿流体）。对于一般的流动，假设：①运动流体的应力张量在运动停止后趋于静止流体的应力张量，于是pij= -pδij+τij，式中pij为应力张量;p为压力；δij为克罗内克符号;τij为偏应力张量；②偏应力张量τij的各分量是速度梯度张量
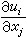各分量的线性齐次函数（这个假设是牛顿粘性公式逻辑上的推广）；③流体是各向同性的。由此可以推出应力张量和变形速率张量sij的关系：
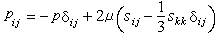。动量方程和能量方程 动量方程是动量守恒的数学表达式，它的矢量形式为：
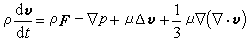，式中v为速度矢量;F为作用在单位质量上的质量力;p为压力;ρ、μ分别为流体密度和动力粘性系数。上式表明单位体积上的惯性力等于单位体积上的质量力加上单位体积上的压力梯度和粘性应力。能量方程是能量守恒的数学表达式，它可以写成：
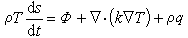，式中T、s分别为流体的热力学温度和单位质量流体的熵；k为热导率；q为由于辐射或其他原因在单位时间内传入单位质量流体中的热量；ф为粘性耗损函数，其表达式为
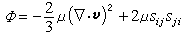，式中sij为变形速率张量。能量方程表明粘性耗损掉的机械能以及由于热交换或其他原因传入的热量使流体的熵增加。涡旋的动力学性质 涡旋的动力学性质主要体现在开尔文定理和亥姆霍兹定理上。如果流体是无粘性、正压的（见正压流体），且外力有势，则涡旋不生不灭，而且涡线、涡管总是由相同的流体质点组成，涡管强度不随时间变化。只有流体的粘性、斜压性和外力无势这三个因素才能使涡旋产生、发展变化和消亡。
伯努利积分和拉格朗日积分 无粘性的、正压的流体在有势外力作用下，其运动方程在定常和无旋两特殊情形下可以积分出来。运动方程的这两个第一积分分别称为伯努利积分（见伯努利定理）和拉格朗日积分。它们（特别是伯努利积分）无论在流体力学的理论研究或实际应用上都十分有用。
动量定理 对于大部分流体力学问题，为了了解整个流场的情况，需要在一定的初始条件和边界条件下解微分形式的流体力学基本方程组。但是，有时只需要知道某些整体性的特征量（例如流体对于在其中运动着的物体的反作用力和整个流动系统的能量损失等），就可以利用积分形式方程组中的整体性定理──动量定理和动量矩定理，根据边界上给定的流动参数直接求出感兴趣的特征量，而不需要解微分方程。上述方法简单易行，在流体动力学中有着广泛的应用。定常运动时的动量方程和动量矩方程采取下列形式：
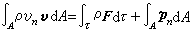， (1)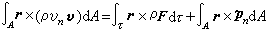
， (2)式中A和τ为任取的控制面及其所包围的体积;vn为A面上流体的法向速度分量;
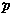n为τ外流体或固体作用在A面上的应力；r为A面上各点的矢径。在非定常运动情形，式(1)和(2)中还应包含体积分
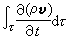和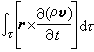
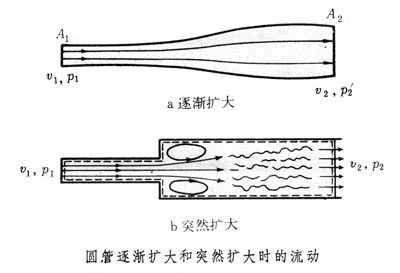
，这两个积分只有在解出微分形式流体力学基本方程组后才能算出，因此，在非定常运动情形，不能应用动量定理和动量矩定理。现以圆管突然扩大时的能量损失问题为例，说明动量定理的应用。对于圆管从截面积A1逐渐扩大到截面积A2的情况(图a)，
根据伯努利积分，有：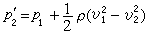
， (3)式中p1、v1和p娦、v2分别为A1和A2处的压力和速度。考虑截面积为A1的小管突然扩大为截面积为A2的大管时的情形(图b)。流体从小管涌出，在边角附近产生涡旋，并与周围流体不断掺混。混合后的流体，过一段距离又以几乎均匀的速度v2继续在大管内流动。涡旋的产生和掺混过程将伴随着机械能的损失。因管突然扩大时，大管中流体的动能与管逐渐扩大时大管中流体的动能相等，所以同管逐渐扩大相比，管突然扩大时流体的机械能损失主要体现在大管内的压力p2小于p娦。p娦-p2表征机械能损失的程度。一般说来，要计算p娦-p2，必须知道突然扩大的管中掺混过程的详细情况，而获得这方面数据是很困难的。但是利用动量定理可以很容易地求出压力损失，而不必追究管内流体运动的详细过程。取图b所示虚线为控制面，根据动量定理，得：p2＝p1-ρv2(v2-v1)。 (4)由式(3)和式(4)，再利用连续性方程v1A1=v2A2，就可得到：
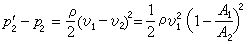，A1/A2越小，压力损失越大，但最大不超过
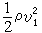。各类流体运动 流体的运动根据不同的标准可分为：层流和湍流；边界层流动（见边界层）和外部位势流动；无粘性流动和粘性流动；不可压缩流动和可压缩流动等等。分述如下：
①观察圆管内或边界层内的定常流动，发现粘性流体运动存在着两种性质截然不同的运动形态，即层流和湍流。层流的特征是流体运动平滑规则，相邻流体分层滑动互不掺混，流体质点的迹线（见流线）光滑，而且流场稳定，没有或很少有脉动。湍流的特征则完全相反，流体呈极不规则的涡旋型流动，各部分流体激烈掺混，伴随着横向动量、质量、能量的传递，质点的迹线杂乱无章，而且流场随机脉动，极不稳定。层流和湍流在一定条件下可以相互转化（见流体运动稳定性）。
②根据L.普朗特的理论，对于高雷诺数的流体运动，粘性的作用局限在物面附近很薄的一层内，这个薄层称为边界层。边界层以外的流体运动可以看作是无粘性的。于是问题可化为先求解边界层外的无粘性流动的速度和压力，然后再研究边界层流动，将粘性和壁面粘附条件考虑进去。研究边界层流动具有特别重要的意义，因为物体表面的摩擦阻力和流动分离形成压差阻力等都取决于边界层内的流动特性。
③普朗特的边界层理论为研究无粘性流动的合理性提供了理论依据。将流动分为无粘性流动和粘性流动不仅为理论研究所必需，而且也具有实际意义。
④当气体流动速度较低时，密度变化不大，气体和液体一样可近似地按不可压缩流体处理。如果气流的速度超过大约声速的40％或者考虑特殊条件下的液体运动（如水下爆炸、水击、波在水中传播等），则必须考虑气体和液体的压缩性影响。
近年来，由于科学技术的飞速发展，形成了一系列流体力学的新分支学科，如物理－化学流体动力学、电流体动力学、磁流体力学、生物流体力学、（见生物流变学）、爆炸力学、地球流体力学、旋转流体和分层流体流动、非牛顿流体力学、多相流体力学、宇宙气体动力学、相对论流体力学等。