流体运动学(卷名：力学)
fluid kinematics
流体力学的一个分支。研究流体运动的几何性质，而不涉及力的具体作用。流体运动学包括下述内容：
流动的分析描述 在流体力学中描写运动的方法有两种，即拉格朗日方法和欧拉方法。拉格朗日方法着眼于流体质点（见连续介质假设），设法描述每个流体质点的位置随时间变化的规律。通常利用初始时刻流体质点的直角坐标或曲线坐标 a、b、c作为区分不同流体质点的标志。 流体质点运动规律可表示成方程(1)的形式：
r＝r (a，b，c，t)， (1)其中r是流体质点的矢径；t为时间；变数a、b、c、t统称为拉格朗日变数。对时间t求式(1)的一次偏导数和二次偏导数，可分别得到流体质点的速度矢量和加速度矢量。欧拉方法着眼于空间点，设法在空间的每一点上描述出流体运动随时间的变化状况。通常用速度矢量
表示流体运动。于是欧拉方法中流体质点的运动规律可表为下式：＝(r，t)， (2)变数r、t 称为欧拉变数。式(2)确定的速度函数是定义在时间t和空间点上的，所以它是场。由式(2)，可按下式求出加速度（见随体导数）：
。虽然拉格朗日方法和欧拉方法都能描述流体的运动，但在流体力学中，人们广泛采用欧拉方法，较少采用拉格朗日方法，这是因为用欧拉变数得到的是场，可以运用研究得很充分的场论知识；而在拉格朗日方法中，由于式(1)不是场，所以无此优点。其次，在欧拉方法中，由于加速度是一阶导数，所以运动方程组是一阶偏微分方程组，它比拉格朗日方法中的二阶偏微分方程组容易处理。流动的几何描述 在拉格朗日方法中，流体质点运动规律的几何表示是迹线。在欧拉方法中，则利用流线几何地描述流体的运动。在非定常运动中，流线和迹线一般是不重合的；而在定常运动中，两者必然重合（见流线）。
流动的分析 流体运动要比刚体运动复杂，因为它除了平动和转动外，还要发生变形。流体微团运动分析的主要内容包含在亥姆霍兹速度分解定理中。
流动的分类 以运动形式为标准，流体运动可分为无旋运动和有旋运动。若在整个流场中墷×
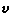=0，则称此运动为无旋运动，反之称为有旋运动。以时间为标准，流体运动可分为定常运动和非定常运动。若所有物理量皆不依赖于时间t，则称此运动为定常运动，反之称为非定常运动。以空间为标准，根据有关物理量依赖于一个曲线坐标、二个曲线坐标和三个曲线坐标，流体运动可分为一维运动、二维运动和三维运动。平面运动和轴对称运动是二维运动的两个重要例子。在直角坐标系Oxyz中，满足w＝0，
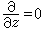的流动称为平面运动，其中w是速度矢量在z轴的分量。在柱坐标系（r，嗞，z）中满足
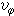＝0，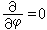
，或球坐标系(r，嗞，θ)中满足
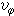＝0，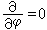
的流动称为轴对称运动，其中
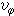是速度矢量在嗞轴的分量。涡旋的运动学性质 涡管的运动学性质为：涡通量在涡管所有横截面上都等于同一常数，称之为涡管的强度。涡管不能在流体内产生或终止，如果它不以涡环的形式存在，就只能延伸到边界上。
区域中有涡和源的分布，就会诱导出速度场。知道涡旋场和散度场求速度场的问题归结为解方程(3)：
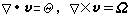， (3)式中嘷和Ω是区域τ内给定的源和涡的强度分布函数。其解为：
式中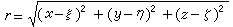 
；ξ、η、ζ是变动点坐标。连续性方程和流函数 连续性方程是质量守恒定律的数学表达式，它的一般形式为（见流体力学基本方程组）：
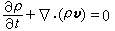或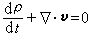 
。对于定常运动和不可压缩流体，连续性方程可简化为：
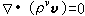，式中ν=0和ν=1分别对应不可压缩流体和定常运动。对于平面和轴对称运动，由连续性方程推出，存在着流函数Ψ，使
， （平面运动）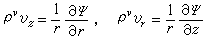
， （轴对称运动）式中u、v，vz、vr分别是速度矢量在直角坐标(x，y，z)和柱坐标(r，嗞，z)中的分量。无旋运动和速度势 根据运动的无旋性墷×
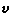＝0推出存在着速度势ф，使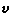=墷ф。在不可压缩流体情形，速度势满足拉普拉斯方程(见拉普拉斯无旋运动，速度势)。参考书目
G. K. Batchelor， An Introduction to Fluid Dynamics，Cambridge Univ.Press，Cambridge，1970.