狄利克雷L函数(卷名：数学)
Dirichlet L-function
又称对应于模q的特征ⅹ(n)的狄利克雷L函数， 即函数
，其中q≥1，ⅹ(n)是模q的一个特征，复变数s=σ+it，σ>1。它在q=1时就是黎曼ζ函数。这类函数最初是由P.G.L.狄利克雷在研究算术级数中的素数分布问题时引进的。它的性质和作用，都与黎曼ζ函数类似，在许多数论问题中有重要应用。它的主要性质有：① 当σ>1时，
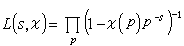，式中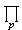
表示对全体素数求积。因而L(s，ⅹ)≠0 (σ>1)。② 当ⅹ0是模q的主特征时，
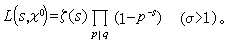于是，通过ζ(s)就把L(s，ⅹ0)解析开拓到全平面。③ 当ⅹ是模q的非主特征时，一定存在惟一的一个模q*，使当σ>1时，有
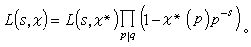
④ 当ⅹ是模q的原特征时，L(s，ⅹ)可解析开拓为整函数，且满足函数方程
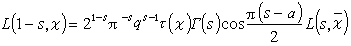，式中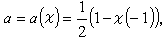
τ(ⅹ)为仅与ⅹ有关的常数，且满足
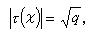塣表ⅹ的共轭特征，即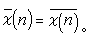
⑤ 对任意的模q的特征ⅹ，有L(1，ⅹ)≠0。
⑥设ⅹ是模q的原特征，那么s=-(2n+α(ⅹ))(n =0，1，2，…)是L(s，ⅹ)的一级零点，称为“无聊零点”；L(s，ⅹ)可能有的其他零点（称为“非无聊零点”）一定都位于带形区域0≤σ≤1中;L(s，ⅹ)确有无穷多个非无聊零点。
⑦ 设T >0，以N(T，ⅹ)表 L(s，ⅹ)在区域0≤σ≤1，｜t｜≤T 中的零点个数。因此，当ⅹ 是模q的原特征和T≥2时，有
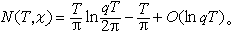
⑧ 设T>0，
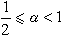，以N(α，T，ⅹ)表L(s，ⅹ)在区域α≤σ≤1，｜t｜≤T中的零点个数。再设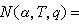
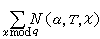，其中Σ表对模q的所有特征求和。因此，当 T≥2时，有
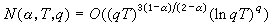。此结果已被改进和推广，通常称之为 L函数的零点密度定理。⑨ 在直线σ=1上，L(s，ⅹ)≠0。由此，对任意固定的q，可推出算术级数中的素数定理。
⑩ 存在绝对正常数X1，使得对任意固定的模q，在所有的函数L(s，ⅹ)(ⅹ mod q)中，仅可能除去一个例外函数外，均在区域
内无零点。如果这样的例外函数L(s，塣)存在，那么塣一定是模q 的实的非主特征，且 L(s，塣) 在上述区域内只有一个一级实零点戓 。这一性质是狄利克雷L函数与黎曼ζ函数的一个主要差别。研究对应于实特征的L函数的实零点，是L函数论的最重要问题之一。 A. 佩奇于1935年证明了：存在绝对正常数X2，使得对任意的实原特征ⅹ modq，q≥3，必有 L(1，ⅹ)≥X2q-1/2。由此可推出，存在绝对正常数X3，使得对任意的实特征 ⅹ mod q，q≥3，当
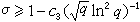时，L(σ，ⅹ)≠0。 C.L.西格尔于1936年证明了：对任给的正数ε，存在正常数c3(ε)，使得对任意的实原特征ⅹmodq， q≥3，必有
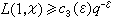。由此推出，对任给正数ε，必有正常数 c4(ε)，使得对任意的实特征 ⅹ modq，q≥3，当
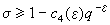时，L(σ，ⅹ)≠0。C. L. 西格尔的结果虽然优于A. 佩奇的结果，但是常数X3(ε)和X4(ε)至今没有办法计算出来。
从性质⑩、、可推得有余项估计的算术级数中的素数定理（见素数分布）。类似于黎曼假设，有所谓广义黎曼假设，即猜测所有的狄利克雷L函数的非无聊零点都位于直线σ=1/2上，通常简记作GRH。大量的数值计算以及理论上的探讨都支持这一假设，但它至今还没有被证明或否定。从GRH可推出一系列重要的数论结果，虽然都是一些假设性的结果（其中有的已被无条件地证明了），但是却指出了研究 L函数零点的重要意义和方向。
参考书目
K.Prachar，Primzahlverteilung，Springer-Verlag， Berlin，1957.
H.Davenport，Multiplicative Number Theory，2nd ed.，Springer-Verlag， Berlin， 1980.