矩阵力法(卷名:土木工程)
matrix force method
按力法的基本原理,以矩阵为数学工具,计算结构的内力和位移的方法,是结构矩阵分析方法中的一种。
结构矩阵分析方法需将结构离散成有限数目的单元进行计算。矩阵力法中常用的单元形式为简支式和悬臂式,这两种单元较为简单,其中尤以简支式为常见。当单元承受非结点荷载时,可用等效结点荷载代替。其方法是将单元间的分界结点视为固定求出固端反力,然后反其向作用在结点上。
矩阵力法的基础是力法,计算超静定结构时要选取基本体系和基本未知力。选取的方法有两种:一种是根据结构的具体情况由计算者选取,并在人为选定的基本体系的基础上计算;另一种是把力法和线性代数中关于秩的知识结合起来,先建立结点平衡方程式,然后利用约当消去法,使多余的基本未知力自动分离出来,这种分析方法称为秩力法。由于前一方法与力法结合较为紧密,故较易了解和常用。
将原有荷载和基本未知力均视为外力时,可以得出结点作用力列矩阵
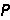 、结构基本未知力列矩阵
、结构基本未知力列矩阵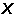 与单元基本未知力(杆端力)列矩阵
与单元基本未知力(杆端力)列矩阵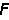 的关系式如下:
的关系式如下: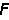 =
=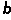 P
P +
+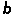 X
X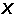 (1)式中
(1)式中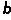 P和
P和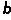 X 分别表示结点作用力
X 分别表示结点作用力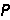 和结构基本未知力
和结构基本未知力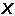 对基本体系的内力影响矩阵。
对基本体系的内力影响矩阵。单元基本未知力
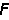 与相应杆端位移
与相应杆端位移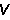 之间的关系式为
之间的关系式为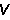 =
=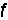 m
m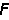 (2)式中
(2)式中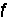 m为未装配结构的柔度矩阵,它等于各单元柔度矩阵
m为未装配结构的柔度矩阵,它等于各单元柔度矩阵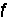 (i)作为子块的对角矩阵。而杆端位移
(i)作为子块的对角矩阵。而杆端位移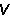 与结点的荷载方向的位移
与结点的荷载方向的位移 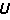 (包括结点作用力和基本未知力在荷载方向的位移
(包括结点作用力和基本未知力在荷载方向的位移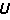 P和
P和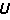 X的关系式为
X的关系式为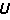 =
=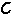
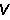 (3)式中
(3)式中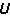 =[
=[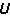 P嗈
P嗈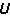 X]T;
X]T;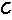 为杆端位移对结点的荷载方向位移的变换矩阵。根据虚功原理,可得
为杆端位移对结点的荷载方向位移的变换矩阵。根据虚功原理,可得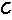 =[
=[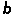 P嗈
P嗈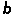 X]T。
X]T。根据上面三式,可以得到
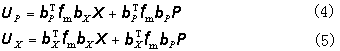
根据相应于基本未知力方向的变形协调条件,
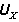 =0,可得到式中
=0,可得到式中 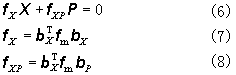
式(6)中
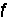 X称为已装配结构的柔度矩阵,即一般力法基本方程中的系数矩阵δ,而
X称为已装配结构的柔度矩阵,即一般力法基本方程中的系数矩阵δ,而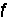 P
P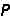 即一般力法基本方程中的自由项矩阵
即一般力法基本方程中的自由项矩阵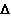 P,因而式(6)即为力法基本方程的矩阵表达式。由(6)即可求得
P,因而式(6)即为力法基本方程的矩阵表达式。由(6)即可求得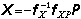 ,代入(1)和(4)式,即得单元基本未知力
,代入(1)和(4)式,即得单元基本未知力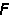 和结点荷载方向位移
和结点荷载方向位移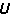 P。既得列矩阵
P。既得列矩阵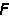 ,由平衡条件可求出单元全部杆端力列矩阵
,由平衡条件可求出单元全部杆端力列矩阵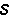 为
为 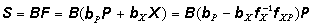 (9)式中
(9)式中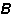 为单元基本未知力对单元全部杆端力的变换矩阵。实际杆端力矩阵为
为单元基本未知力对单元全部杆端力的变换矩阵。实际杆端力矩阵为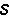 a应由(9)式再叠加单元非结点荷载引起的固端力矩阵
a应由(9)式再叠加单元非结点荷载引起的固端力矩阵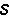 f。第i单元实际杆端力矩阵应为
f。第i单元实际杆端力矩阵应为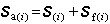 (10)
(10)矩阵力法计算杆端力步骤为:①选取基本体系和基本未知力;②划分单元,并求出等效结点荷载;③求出单元柔度矩阵
 i,并构成
i,并构成 m;④求出
m;④求出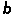 X、
X、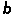 P,并由(7)(8)式求出
P,并由(7)(8)式求出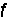 X、
X、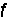 P;⑤由(9)式求出全部杆端力
P;⑤由(9)式求出全部杆端力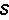 ,从而由(10)式求出实际杆端杆力
,从而由(10)式求出实际杆端杆力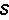 a。
a。用矩阵力法求静定结构的位移时,由公式(4)令基本未知力X=0,即可得静定结构结点荷载方向位移的公式为
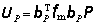 (11)
(11) 在超静定结构分析中,由于矩阵力法的基本未知数是多余力,因而在计算超静定次数较少的结构时较为合适。不过采用矩阵力法很难编制出适用于各种结构的大型通用程序。所以目前常采用基本体系的单元形式统一的矩阵位移法进行分析。
参考书目
普齐米尼斯基著,王德荣等译:《矩阵结构分析理论》,国防工业出版社,北京,1974。(J.S.Przemieniecki,Theory of Matrix Structural Analysis,McGraw-Hill, New York,1968.)