椭圆函数(卷名：数学)
elliptic function
双周期的亚纯函数。它最初是从求椭圆弧长时引导出来的，所以称为椭圆函数。椭圆函数论可以说是复变函数论在19世纪发展中最光辉的成就之一。N.H.阿贝尔、C.G.J.雅可比和K.外尔斯特拉斯等人对此都有卓越的贡献。 一个函数ƒ(z)，如果存在着常数T≠0（可以是复数），使对一切z均有
ƒ(z+T)=ƒ(z) (1)则称ƒ(z)为周期函数，T为其周期。可使周期T满足式(1)且有最小的模。
如果一函数ƒ(z)有两个周期2ω，2ω′，且
（以下恒设其>0），则称ƒ(z)为双周期函数。一般说来，ƒ(z)在z=z0附近的性态与在
附近的性态相同，m，n为任何整数;z0+
称作z0的(周期)合同点。因此，研究ƒ(z)例如可只限于z在以0，2ω1=2ω，2ω2=2(ω+ω′)，2ω3=2ω′为顶点的平行四边形p中变动。这个平行四边形称为ƒ(z)的基本周期四边形或基本胞腔（见图
）。只有极点的双周期解析函数ƒ(z)就是椭圆函数。不妨假设在p的周界上没有ƒ(z)的零点和极点，因为否则只要对复坐标z作适当平移变换便可达到目的。
由刘维尔定理知，双周期解析函数ƒ(z)如果没有奇点则必为常数。又由留数定理易证，ƒ(z)在p 中也不可能只有一个单极点。且可证明，ƒ(z)在p 中取任何值的点的个数包括极点的个数（重数也计入个数内）均相同。椭圆函数在p中极点的个数称作它的阶数。因此，（非常数的）椭圆函数至少是二阶的。
ξ函数与P函数 定义
(2)式中∑′表示对一切整数m，n求和，但m=n=0除外。ξ(z)是一亚纯函数，以
为单极点(m，n=0，±1，±2，…)，且主部为
。它不是周期函数，但满足下列关系：
(3)式中ηj=ξ(ωj)为三个常数，它们之间有如下关系：
由式(3)可见
已是一个二阶椭圆函数，以
为二阶极点，并以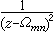
为其主部。任何椭圆函数均可通过 P(z)及其各阶导函数表出。
函数P(z)满足微分方程
式中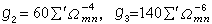
。P函数还有所谓加法公式
σ函数 为了得到椭圆函数的一种方便的表示法，引进σ函数。
，式中∏′表示对一切整数m，n求积，但m=n=0除外。σ(z)是以
为单零点的整函数，它不是双周期的，但满足下列关系：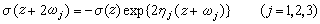
易证
任何 n阶椭圆函数ƒ(z)，如分别以α1，α2，…，αn和β1，β2，…，βn为其零点和极点（计入重数），则总可使得
，这时它可表为
式中C为一常数。如记
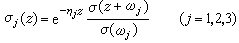，则可证
式中
，且根式已适当选定一支。θ函数 在实际应用中，作变换
，可使椭圆函数ƒ(z)变成另一椭圆函数φ(υ)，后者的一个周期为1，另一周期为
。引进θ函数
式中q=
。θ(υ)不是椭圆函数，但有
由θ(υ)还可引进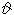
函数如下：
这些函数都不是椭圆函数，但有
任何以2ω，2ω′为周期的椭圆函数ƒ(z)，可通过θ函数表出：
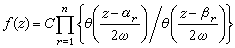如前式中αr，βr(r＝1，…，n)为ƒ(z)的零点与极点。P(z)与
k(υ)间有如下确定的关系：
式中
。
k 函数间也有加法公式等。雅可比椭圆函数 令
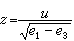(根号取定一值)，定义雅可比椭圆函数如下：
它们都是 u的二阶椭圆函数。sn u以 4K与2iK′为周期，cnu以4K与2K+2iK′为周期，dn u以2K与4iK′为周期，式中
。它们和三角函数有某些相似之处。例如，有
，
等等。由这些公式，可得
，这里根式应选取u＝0时取值 ＋1的一支，由此可以得出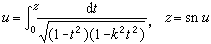
(4)右边这类含有四次根式的积分正是求椭圆的弧长时会遇到的那种类型，它们统称为椭圆积分。由式(4)可见，u作为z的函数时，其反函数正好是椭圆函数sn u。椭圆函数名称来源于此。自守函数 椭圆函数 ƒ(z)具有这样一个特点：当z经过平移变换
后函数值不变。变换T，T′生成一群G，ƒ(z)的变量z经G中任何变换后ƒ(z)保持不变。一般说来，设G =｛T｝为分式线性变换构成的群(但不是单位群，即不是由恒等变换一个元构成的群)，又设ƒ(z)为某区域D中的亚纯函数，群G中的任何元T把D变成自身。且使
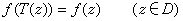，则称ƒ(z)为区域D中关于群G的自守函数。椭圆函数就是全平面中关于群
整数}的自守函数。自守函数理论是由H.庞加莱与F.克莱因等人在19世纪80年代建立起来的，它对复变函数论的许多分支以及微分方程都有重要影响。