积分方程(卷名：数学)
integral equation
积分号下含有未知函数的方程。其中未知函数以线性形式出现的，称为线性积分方程；否则称为非线性积分方程。
积分方程起源于物理问题。牛顿第二运动定律的出现，促进了微分方程理论的迅速发展，然而对积分方程理论发展的影响却非如此。1823年，N.H.阿贝尔在研究地球引力场中的一个质点下落轨迹问题时提出的一个方程，后人称之为阿贝尔方程，是历史上出现最早的积分方程，但是在较长的时期未引起人们的注意。“积分方程”一词是 P.du B.雷蒙德于1888年首先提出的。19世纪的最后两年，瑞典数学家（E.）I.弗雷德霍姆和意大利数学家V.沃尔泰拉开创了研究线性积分方程理论的先河。从此，积分方程理论逐渐发展成为数学的一个分支。
1899年，弗雷德霍姆在给他的老师（M.）G.米塔－列夫勒的信中，提出如下的方程
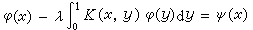， (1)式中φ（x）是未知函数；λ 是参数，K（x，y）是在区域0 ≤x，y ≤1上连续的已知函数；ψ(x)是在区间0≤x ≤1上连续的已知函数。并认为方程（1）的解可表为关于λ 的两个整函数之商。1900年，弗雷德霍姆在其论文中把（1）称为“积分方程”， 并初次建立了K（x，y）的行列式D(λ)和D（x，y，λ），证明了它们都是 λ的整函数， 以及当 λ是 D(λ)的一个零点时， 则(1)的齐次方程φ
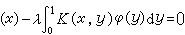有不恒等于零的解。1903年，他又指出，若行列式D(1)≠0，则有一个且只有一个函数φ(x)满足方程(1)(λ=1)，此时φ(x)可表为
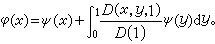从此，积分方程理论的发展进入了一个新的时期。以下形式的积分方程
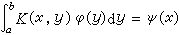， (2)
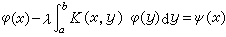， (3)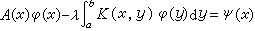
， (4)分别称为第一种、第二种、第三种弗雷德霍姆积分方程，其中K(x，y)是在区域α≤x、y≤b上连续的已知函数，称为方程的核;A(x)、ψ(x)都是在区间α≤x ≤b上连续的已知函数，φ(x)是未知函数，λ是参数。第一、二种弗雷德霍姆积分方程是第三种弗雷德霍姆积分方程的特殊情形。但是，第一种方程与第二种方程却有本质上的区别。
与弗雷德霍姆几乎同时，沃尔泰拉研究了如下形式的积分方程
(5)
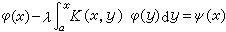， (6)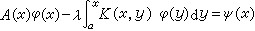
， (7)分别称为第一种、第二种、第三种沃尔泰拉积分方程，式中λ、φ(x)、ψ(x)和A(x)如前所述，K(x，y)是定义在三角形区域α≤y≤x≤b上的已知连续函数。弗雷德霍姆积分方程中的核K(x，y)当x<y时为零，就是沃尔泰拉积分方程。因此沃尔泰拉积分方程是弗雷德霍姆积分方程的特殊情形。但是这两类方程的本质是不同的。例如，第二种沃尔泰拉积分方程对于一切λ 值总可用迭代法求解，而第二种弗雷德霍姆积分方程却出现了特征值问题；又如，第一种沃尔泰拉积分方程在一定条件下可以化为等价的某个第二种沃尔泰拉积分方程，而第一种弗雷德霍姆积分方程的讨论却困难得多。弗雷德霍姆积分方程和沃尔泰拉积分方程的理论可以推广到多个未知函数的方程组的情形。这时只需要把φ(x)视为未知函数向量φ(x)=(φ1(x)，φ2(x)，…，φn(x))，K(x，y)看作n阶方阵(Kij(x，y))，i，j=1，2，…，n，ψ(x)=(ψ1(x)，ψ2(x)，…，ψn(x))看作已知函数向量。
D.希尔伯特和E.施密特对第二种弗雷德霍姆积分方程做了重要的工作，特别是关于对称核积分方程的特征值存在性，对称核关于特征函数序列的展开，以及希尔伯特 -施密特展开定理等。至于第一种弗雷德霍姆积分方程，早在1828年就为G.格林在研究位势理论以解决拉普拉斯方程的狄利克雷问题时所导出。格林当时还指出，关于这类方程没有一般的理论。20世纪初，E.施密特得到了方程(2)有解的必要条件。其后(C.-)É.皮卡指出，该条件在核K(x，y)的特征函数序列是完备时也是充分的。但是，这一结果并没有提供一个一般的方便解法。第一种弗雷德霍姆积分方程的系统理论，尚未建立。
积分方程的核常是非连续的。例如，在一维空间，核K(x，y)是具有如下形式：
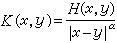，式中0<α<1，H(x，y)是有界函数。这样的核称为弱奇性核，相应的方程称为弱奇性方程。可以证明，对弱奇性核施行如下运算：
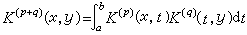，（p、q 都是正整数，K(1)(x，y)呏K(x，y)，经m 次后，只要
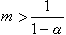，就得到一个有界核K(m)(x，y)，而弱奇性消失了。由此可以证明，具有弱奇性核的积分方程同样具备第二种弗雷德霍姆积分方程的一切性质。对于n 维空间的积分方程，也可以建立相应的结论。奇异积分方程是与弗雷德霍姆积分方程有本质区别的一类方程。常见的奇异积分方程有两种：一种是核具有主值意义的奇性，例如柯西核；一种是积分区域为无穷的积分方程，例如维纳－霍普夫方程。
前一种奇异积分方程的理论是在弗雷德霍姆积分方程理论建立后的几年中产生的。希尔伯特在研究解析函数的边值问题中发现了这种奇异积分方程。几乎同时，（J.-）H.庞加莱在研究潮汐现象时，也发现了它。他们的工作为这种方程奠定了理论基础。这种奇异积分方程的一般形式为
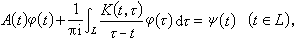式中l是平面上光滑闭围道，系数A(t)、K(t，τ)和ψ(t)都是给定的在 l上按赫尔德意义连续的函数。方程中的积分在通常意义下是发散的，但在一定假设下，其柯西主值存在。这样的方程称为具有柯西核的奇异积分方程。此外，如下具有希尔伯特核的方程
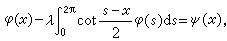也是一种主值意义下的奇异积分方程。对于这种奇异积分方程的研究成果及应用，苏联数学家Η.И.穆斯赫利什维利于1946年发表的专著《奇异积分方程》作了系统的总结。后一种奇异积分方程的重要例子是维纳－霍普夫方程。它是20世纪20年代初在大气辐射传输问题的研究中首先得到的，在许多实际问题中有重要的应用。
相应于弗雷德霍姆定理，对于上述两种奇异积分方程有诺特定理（见奇异积分方程）。
近年来，非线性积分方程的研究，有了很快的发展。例如哈默斯坦型积分方程，即如下形式的非线性积分方程
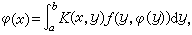式中 K(x，y)、ƒ(y，u)都是已知函数，ƒ(y，u)关于u是非线性的。自H.哈默斯坦于1930年提出以来，研究者不乏其人，而且已得到不少有意义的结果。对于非线性奇异积分方程也有不少结果，但是直到现在，对于一般的非线性积分方程还没有系统的理论，即使是可解性的讨论也很困难。自抽象空间这个概念创立以来，如希尔伯特空间、巴拿赫空间以及算子理论的建立，使古典的积分方程以崭新的面貌出现。例如，把积分方程(3)中出现的函数看作是巴拿赫空间X的元素，原来的积分运算以算子T代替，于是方程(3)就可写为
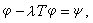(8) 这里T是巴拿赫空间X中的一个全连续算子，ψ是X中一个已知元素，而φ是X中的未知元素。方程(8)的齐次方程φ-λTφ =0，若对于某些λ值有不等于零元素的解，则称这些λ值为算子T的点谱， 相应的元素称为特征元素。对于方程(8)也有在巴拿赫空间X中类似的弗雷德霍姆定理。算子T的谱分解是重要的研究课题，J.冯·诺伊曼在这方面有丰硕的研究成果。积分方程有广泛的应用。微分方程某些定解问题的求解可归结为求解积分方程。例如，为求解常微分方程初值问题
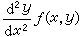，y(x0)=y0，y′(x0)=y1，只要在微分方程两端积分两次，并交换积分次序和利用初始条件，就得到与之等价的沃尔泰拉积分方程
类似地，对于常微分方程的边值问题也可得到与之等价的弗雷德霍姆积分方程。又如，偏微分方程中拉普拉斯方程的狄利克雷问题和诺伊曼问题，可分别利用双层位势和单层位势作为中介而归结为第二种弗雷德霍姆积分方程的求解，而且是等价的。粘性流体力学问题中的维纳- 斯托克斯方程的定解问题也可化为非线性积分方程组。这种利用位势求解微分方程的某些定解问题的方法，已有很多推广，有相当多的一阶或二阶椭圆型方程组的某些边值问题，引进类似于位势的积分算子，往往可归结为弗雷德霍姆积分方程或奇异积分方程。在地质学中制作地球内部的精细三维图问题。这种图对勘探矿产、预报地震等等都很需要，但不能采用实验的方法来制作，而只能采取间接的方法解决，一般是借助尖端的精密仪器和人造卫星精确地定出地球外部点处的地球引力位势，再利用引力位势的方法归结出关于地球内部密度的第一种弗雷德霍姆积分方程。在空气动力学中研究分子运动，考虑非均匀流体中悬浮晶粒的布朗位移和热扩散，导致了以柯尔莫哥洛夫命名的一类积分方程。在确定飞机机翼的剖面时，需要对环流、升力、阻力等等效应进行计算，也往往导致一个积分方程。其他如中子迁移、电磁波衍射以及经济学与人口理论等都导致奇异积分方程的研究。
中国有不少学者致力于积分方程的理论和应用方面的研究，得到了许多有意义的结果。