迭代法(卷名：数学)
iterative method
一类利用递推公式或循环算法构造序列求问题近似解的方法。例如利用关系式
，从x0开始依次计算x1，x2，…来逼近方程x＝ƒ(x)的根x
的方法和由关系式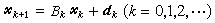
近似求解线性代数方程Ax=b的方法都是迭代法。一般，利用递推关系式 
，构造序列{xk}逼近所论问题解x
的方法称为迭代法，Ψk称为迭代算子或迭代函数，｛xk｝为迭代序列。若xk存在极限
，则称迭代序列收敛。若存在1≤p<
以及正的常数Cp使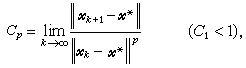
则称迭代序列对于x
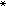具有p阶收敛速度或者说是p阶收敛的。如果对所有由迭代函数Ψk产生的收敛于x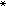的迭代序列｛xk｝，上式均成立，则称此迭代法对于x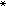是p阶收敛的。对确定的正整数m，迭代算法
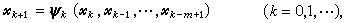称为m步迭代法，当m=1，称为单步迭代法或逐步逼近法，它是最常用的迭代算法。用m步迭代法计算时，需给定m个初始近似x0，x-1，…，x-m+1。若Ψk与k无关，称之为定常迭代法。所有定常迭代法均可化成这种形式。当单步定常迭代法
收敛于x
时，则x为方程组x＝Ψ(x)的解。迭代法研究的主要课题是对所论问题构造收敛的迭代算法，分析它们的收敛速度及收敛范围。迭代法的收敛性定理可分成下列三类：①局部收敛性定理：假定问题解存在，断定当初始近似与解充分接近时迭代法收敛；②半局部收敛性定理：在不假定解存在的情况下，根据迭代法在初始近似处满足的条件，断定迭代法收敛于问题的解；③大范围收敛性定理：在不假定初始近似与解充分接近的条件下，断定迭代法收敛于问题的解。
对于单步定常迭代法有以下基本收敛性定理：
定理1 设在解x
的邻域内，Ψ(x)连续可微，Ψ(x)的谱半径小于1，则当初始近似x0与x充分接近时，单步定常迭代法对于x收敛。定理2 设于区域S={x|‖x-x0‖≤r}内Ψ(x)满足条件：‖Ψ(x)-Ψ（у）‖≤q‖x-у‖，凬x，у∈S，且‖x0-Ψ(x0)‖≤(1-q)r，其中0<q<1，则x=Ψ（x）在S中存在惟一解x
，单步定常迭代法对于x收敛，并有估计式
迭代法在线性和非线性方程组求解、最优化计算以及特征值计算等问题中广泛应用。