算子半群(卷名：数学)
semigroup of operators
依赖于参数的算子族。单参数的算子半群可以通过指数公式exp(-tA)的形式表示出来，其中A是一个算子，称为生成元，而t≥0。算子半群理论是泛函分析的一个分支，主要研究各种类型的算子半群和它们的生成元的特性，以及指数公式的各种表达形式。这个理论在发展型方程（扩散型及波动型偏微分方程）、马尔可夫过程论、算子逼近论、各态历经理论、控制理论以及量子力学的数学理论中有着广泛的应用。
强连续线性算子半群 是这样一族线性算子{T(t)|t≥0}，它们都连续地映巴拿赫空间x于自身，满足：①T(0)=I（恒同算子）；②
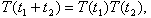对一切t1，t2≥0；③对一切x∈X，有T(t)x→x于x当t↓+0。这类半群可以表示为exp(-tA)的形式，其中A是闭的，有稠密的定义域D(A)，且满足条件：扽ω0>0，当
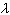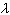>ω0时，I+A有有界逆，并有常数M，使得
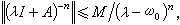n=1，2，…。这个条件还是充分的。指数公式exp(-tA)有几种解释。其一，当x∈D(A)时，成立
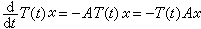。这个结论给出算子微分方程初始值问题的解。
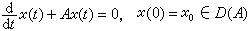，有解x(t)=T(t)x0。其二，
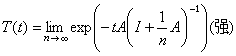，这里若记
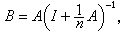
则其为有界线性算子，于是可以定义
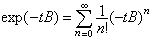。其三，
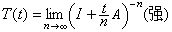。这类算子半群的理论主要是由C.E.希尔、吉田耕作、R.S.菲利普斯等人奠定的。
酉算子群 是希尔伯特空间 H到自身的一族酉算子(见线性算子)，{U(t)│-∞<t<∞}，满足:①
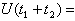
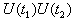对一切实数t1，t2；②对任意x，y∈H，函数(U(t)x，y)是可测的，其中( ，)是H上的内积。斯通定理断言：U(t)＝exp(-itA)， 其中A是H上的一个自伴算子。而且逆定理也成立。这个定理在群表示论中有重要的作用，在量子力学中则给出薛定谔方程解的表示。压缩半群 满足‖T(t)‖≤1，对一切t>0的强连续算子半群。成为压缩半群的生成元A的充要条件是
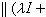
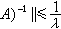，对一切λ>0。线性算子A称为是增殖的，是指
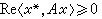对一切x∈D(A)，对一切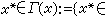
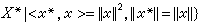，式中〈，〉表示x的共轭空间x
与x 间的对偶。压缩半群的生成元有一个等价的刻画：A是闭的增殖算子，并有λ0>0，使得(λ0I+A)的值域是满的。压缩半群的应用极为广泛，许多具体算子半群都是压缩的。例如：布朗运动中迁移函数导出的算子半群、发展型方程的解导出的算子半群以及泊松核导出的半群等。解析算子半群 还有一类特殊的压缩半群，其中T(t)作为 t的算子值函数可以解析开拓到一个包含正实轴的复平面中的角形区域上去。这类算子半群在抛物型方程中有重要应用。
线性算子半群理论也被推广到了非线性算子。非线性压缩算子半群{T(t)│t≥0}是这样一族由巴拿赫空间x中的子集C到自身C 的非线性映射，除了满足线性强连续算子半群定义中的条件①～③(但以x∈C代替x∈x)而外，还假设满足条件④‖T(t)x-T(t)y‖≤‖x-y‖，对一切x，y∈C，和一切t≥0。为了描写非线性压缩半群的生成元，引进多值增殖算子的概念。称x×x上的一个子集A为一个多值算子，如果记Ax={y∈x|[x，y]∈A}，D(A)={x∈x|Ax≠═}，R(A)=UAx，(见非线性算子)。一个多值算子A称为是增殖的，如果，
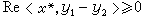对一切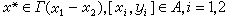
。当x是希尔伯特空间时，一个多值增殖算子就是一个单调算子。多值增殖算子有一个等价刻画：
。当λ>0，对一切[x1，yj]∈A，i=1，2。有下列克兰多尔－利格特定理：设A是巴拿赫空间x上的一个闭的多值增殖算子，并且存在λ>0，使得
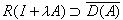，则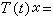
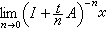对一切t>0及一切
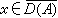都存在，并且T(t)是一个非线性压缩半群。但是其逆命题一般是不成立的。事实上有例子表明：存在着一个没有生成元的压缩半群，即对每个
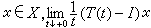都不存在。然而当x是一个希尔伯特空间时，上述定理中的条件相当于A是极大单调的。这时其逆定理在下述意义下成立。设x是一个希尔伯特空间，那么在x 的极大单调算子A与闭凸子集C上的非线性压缩半群之间存在着一一对应如下:①对每个极大单调算子A，存在
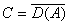上的惟一的非线性压缩半群T(t)，使得 
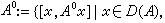A0x是Ax中取极小模的元素}是这半群的生成元;②对每个在闭凸子集C上定义的非线性压缩半群T(t)，存在惟一的极大单调算子A，使得
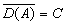，并且A0是T(t)的生成元。非线性半群理论在非线性发展型方程和非线性各态历经理论的研究中有重要的应用。参考书目
E. Hille and R.S.Phillips，Functional Analysis and Semigroups，2nd ed.， American Math.Soc.Colloq. Pub.，New York， 1957.
K.Yosida，Functional Analysis，5th ed.，Springer-Verlag， Berlin， 1978.
H.Brézis，Opérateurs MaxiMaux Monotones et Semigroups de Contractions dans Les Espaces de Hilbert，North-Holland， Amsterdam， 1973.
M. Crandall and T.Liggett， Generation of Semi-groups of Nonlinear Transformations in General Banach Spaces，American Journal of MathMatics，Vol. 93， pp. 265～298， 1971.