通用网论(卷名:电子学与计算机)
general net theory
以条件事件系统为基础,研究网的分类、各类网的性质及其相互关系的理论,是网论分支之一。
条件事件系统(简称CE系统)若限制佩特里网(见佩特里网论)为简单网,且要求它的各个圆圈节点之容量均为1,就可把这些圆圈理解为条件,其中码子的出现与否反映条件是否成立。若这种网的可到达状态集使得任何条件均有成立与不成立的机会,任何事件也都有实施的机会,而且从任一可达状态可以到达任何别的可到达状态,那么这种网就是一个CE系统,一般用(B,E,F,C)表示,其中B,E分别为条件集合及事件集合;F是流关系;C是可到达状态集。这时条件仍用圆圈图示,事件则用方框(□)表示。一般短线代表不能分解的基本事件,方框表示有可能进一步分解的事件(或变迁)。
基本情况 根据佩特里网论规定的变迁实施规则,CE系统中的事件有以下五种基本情况。
① 具备条件。
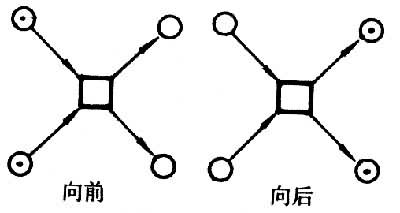
② 发生。
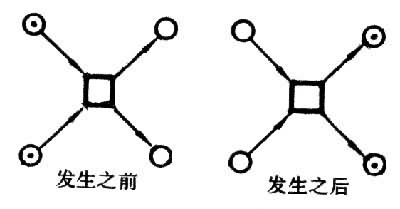
③ 接触:事件之发生将导致某些条件的容量被突破。
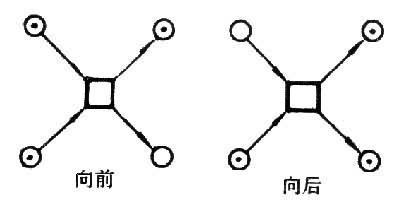
④ 冲突:两个同时具备条件的事件共享输入或输出条件,从而其中任一事件的发生使另一事件不再具备条件。
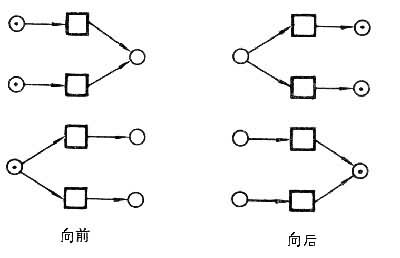
⑤ 迷惑:并发事件引起系统脱离或进入冲突,而且并发事件之发生顺序(这是不可观察的)可能影响系统之行为。
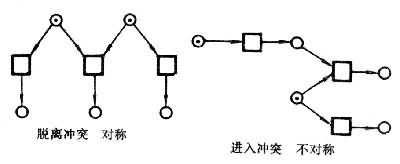
系统的层次 CE系统模拟的是反复运转的系统或子系统。以CE系统为部件构造信息流网,可模拟信息在系统中的流动(表现为码子位置及数量的变化)。将CE系统的实际活动记录下来的是出现网,并发关系则是确定出现网性质(因而CE系统性质)的基础,通用网论试图以此为包括计算机科学在内的多种科学建立一种共同的基础。它的层次关系是:③信息流网、②CE系统、①出现网和
 并发关系。
并发关系。出现网 出现网是不带标识的佩特里网,而且要求流关系F不含循环,要求每个圆圈至多有一个输入地点和一个输出地点。若令出现网节点之集合为X,那么对任何x,y∈X,若x厵y且能沿流关系F从x到y, 就说x小于y,记作x<y。由于F不含循环,所以x<y和y<x不能同时成立。
并发关系 若x,y∈X,但x
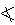 y∧y
y∧y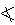 x,就说x和y并发,记作x∝y。CE系统中a,b两件事若同时具备条件且互不冲突,它们是并发的;若a,b为可以同时含有码子的条件,那么它们也是并发的;若a为条件而b为事件,只要a在b发生之前和之后均成立,a和b也是并发的。CE系统两事件间的并发关系可以用它们的同步距离来定量地描述。
x,就说x和y并发,记作x∝y。CE系统中a,b两件事若同时具备条件且互不冲突,它们是并发的;若a,b为可以同时含有码子的条件,那么它们也是并发的;若a为条件而b为事件,只要a在b发生之前和之后均成立,a和b也是并发的。CE系统两事件间的并发关系可以用它们的同步距离来定量地描述。同步距离 若a,b为某CE系统中的两组事件,a,b间的同步距离定义是该系统任何进程中 a组事件发生的次数与b组事件发生的次数之差的绝对值之最大者,若不存在最大值则为无穷。同步距离用 σ(a,b)表示,因为σ 满足距离公理,故称同步距离。交替发生的两事件同步距离为1,并发事件间同步距离≥2。同步距离为1的一切事件偶(a,b)所成立集称为CE系统的最小集合。
网拓扑和网射 将CE系统之进程记录下来,可得到该系统的一个出现网;将出现网折叠,可得其CE系统。折叠是一种网射。网射是保持流关系的网连续映射。这里连续是对网上的拓扑而言的。网拓扑满足通常的拓扑公理,只是将“任意有限个开集的交集仍是开集”这条公理中的“有限”二字去掉。若规定CE系统中的条件为开集,凡同时包含事件及其输入输出条件的集合也是开集,那么CE系统的节点集合满足网拓扑公理。网拓扑又叫佩特里拓扑,其作用是有限个点构成的空间也可以是连续的,通用网论期望借此沟通离散模型和连续模型之间的鸿沟。通用网论已在许多学科获得广泛的应用。