纳维－斯托克斯方程(卷名：力学)
Navier-Stokes equation
描述粘性不可压缩流体动量守恒的运动方程，简称N-S方程。此方程是法国科学家C.-L.-M.-H.纳维于1821年和英国物理学家G.G.斯托克斯于1845年分别建立的，故名。它的矢量形式为：
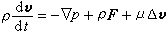。 (1)在直角坐标中，它可写成：
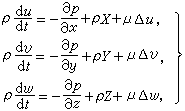(2)式中ρ为流体密度；v为流体速度矢量，在直角坐标中其分量为(u，v，w)；p为流体各向同性压力；F为体积力，在直角坐标中其分量为(X，Y，Z);μ是动力粘性系数。N-S方程概括了粘性不可压缩流体流动的普遍规律，因而在流体力学中具有特殊意义。粘性可压缩流体运动方程的普遍形式为：
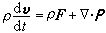， (3)式中
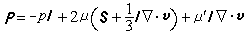， (4)其中
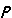为流体应力张量；
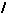为单位张量;
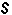为变形速率张量，在直角坐标中其分量为：
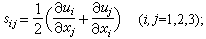μ′为膨胀粘性系数，一般情况下μ′＝0。若流体是均质和不可压缩的，这时μ＝常数，墷·v＝0，则方程(3)可简化成N-S方程(1)和(2)。如果再忽略流体粘性(即μ＝0)，则(1)就变成通常的欧拉方程：
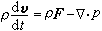， (5)即无粘流体运动方程（见流体力学基本方程组）。从理论上讲，有了包括 N-S方程在内的基本方程组，再加上一定的初始条件和边界条件，就可以确定流体的流动。但是，由于N-S方程比欧拉方程多了一个二阶导数项μΔv，因此，除在一些特定条件下，很难求出方程的精确解。可求得精确解的最简单情况是平行流动。这方面有代表性的流动是圆管内的哈根－泊肃叶流动（见管流）和两平行平板间的库埃特流动（见牛顿流体）。
在许多情况下，不用解出N-S方程，只要对N-S方程各项作量级分析，就可以确定解的特性，或获得方程的近似解。对于雷诺数Re《1的情况，方程左端的加速度项与粘性项相比可忽略，从而可求得斯托克斯流动的近似解。R.A.密立根根据这个解给出了一个最有名的应用，即空气中细小球状油滴的缓慢流动。对于雷诺数Re》1的情况，粘性项与加速度项相比可忽略，这时粘性效应仅局限于物体表面附近的边界层内，而在边界层之外，流体的行为实质上同无粘性流体一样，所以其流场可用欧拉方程求解。
把 N-S方程沿流线积分可得到粘性流体的伯努利方程：
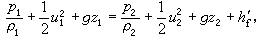(6)式中g为重力加速度;h媕为单位质量流体克服阻力作功而引起的机械能损失。因此，流体沿流线流动时，机械能会转化成热能，使流体温度升高。参考书目
L.普朗特著，郭永怀、陆士嘉译：《流体力学概论》，科学出版社，北京，1981。(L.Plandtl，etal.， Führer Durch die Str-mungslehre，Friedr.Vieweg und Sohn，Braunschweig，1969.)