线性判别函数(卷名：自动控制与系统工程)
linear discriminant function
统计模式识别中用以对模式进行分类的一种最简单的判别函数。在特征空间中，通过学习，不同的类别可以得到不同的判别函数，比较不同类别的判别函数值大小，就可以进行分类。统计模式识别方法把特征空间划分为决策区对模式进行分类。一个模式类同一个或几个决策区相对应。每个决策区对应一个判别函数。对于特征空间中的每个特征向量x,可以计算相应于各个决策区的判别函数gi(x),i=1,2,…,c。用判别函数进行分类的方法就是：若对所有的i均有gi(x)≥gi(x),则把x分为第j类,记成r(x)＝j。对于线性判别函数,gi(x)的函数形式为
gi(x)＝Wi0＋Wi1x1＋Wi2x2＋…＋Widxd式中x1,x2,…,xd是输入模式特征向量的各个分量，Wi0，Wi1,…,Wid组成与第i类对应的权向量，它们的大小反映与它们对应的特征向量的各个分量在确定第 i类判别函数值的重要程度。
特征空间中分别与第i类、第j类相对应的区域之间的决策边界形式为
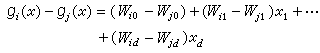对于一个两类分类器,可以计算g(x)＝g2(x)-g1(x)。若g(x)≥0，则r(x)＝2，相应于决策区R2。若g(x)＜0,则r(x)＝1，相应于决策区R1。这一结果可写成
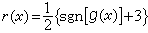式中sgn(Z)是符号函数，在Z≥0时等于1,在Z＜0时等于-1。这样一个两类线性分类器具有图中的形式。
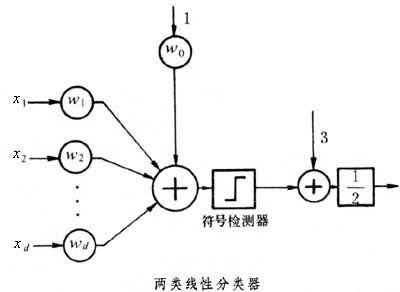人们已研究出多种求取决策边界的算法。线性判别函数的决策边界是一个超平面方程式，其中的系数可以从已知类别的学习样本集求得。F.罗森布拉特的错误修正训练程序是求取两类线性可分分类器决策边界的早期方法之一。在用线性判别函数不可能对所有学习样本正确分类的情况下，可以规定一个准则函数（例如对学习样本的错分数最少）并用使准则函数达到最优的算法求取决策边界。用线性判别函数的模式分类器也称为线性分类器或线性机。这种分类器计算简单，不要求估计特征向量的类条件概率密度，是一种非参数分类方法。当用贝叶斯决策理论进行分类器设计时，在一定的假设下也可以得到线性判别函数，这无论对于线性可分或线性不可分的情况都是适用的。在问题比较复杂的情况下可以用多段线性判别函数（见近邻法分类、最小距离分类）或多项式判别函数对模式进行分类。一个二阶的多项式判别函数可以表示为
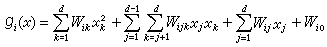与它相应的决策边界是一个超二次曲面。参考书目
R.O.Duda and P.E.Hart，Pattern Classificationand Scene Analysis,John Wiley & Sons，New York,1973.