线性振动(卷名：力学)
linear vibration
系统中构件的弹性服从胡克定律，运动时产生的阻尼与广义速度的一次式成正比的振动。它通常是实际系统微幅振动的一个抽象模型。线性振动系统最根本的特征是：适用叠加原理，即对于线性系统，如果在输入x1作用下，系统响应为y1，而在输入x2作用下，系统响应为y2，则系统在输入x1和x2的联合作用下的响应就是y1+y2。这给线性系统的分析带来极大的方便。在叠加原理的基础上，可以把一个任意的输入分解为一系列微元冲量的和，然后求得系统的总响应。在这一原理的基础上，还可以将一个周期激励经傅里叶变换，展成一系列谐和分量的和；方法是：先分别考察各个谐和分量对系统的作用结果，然后再将它们叠加起来，得到系统的总响应。因此，常参量线性系统的响应特性可用脉冲响应或频率响应描述。脉冲响应是指系统对单位冲量的响应，它表征系统在时域的响应特性。频率响应是指系统对单位谐和输入的响应特性，它表征系统在频域的响应特性。两者由傅里叶变换确定对应关系。
单自由度系统的线性振动 指可用一个广义坐标来确定系统位置的线性振动。它是最简单最基本的振动，许多振动的基本概念和特征可由此引出。它包括简谐振动、阻尼振动和受迫振动。
简谐振动 物体在与位移成正比的恢复力作用下， 在其平衡位置附近按正弦规律作往复的运动（图 1）。
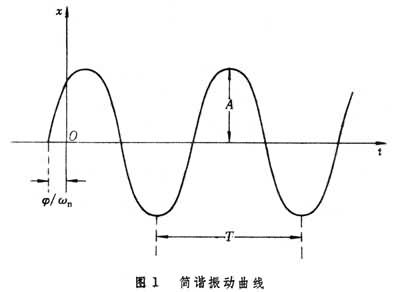以x表示位移，t表示时间，这种振动的数学表达式为：x＝Asin(ωt+嗞)， (1)式中A为位移x的最大值，称为振幅，它表示振动的强度；ωn表示每秒中的振动的幅角增量，称为角频率，也称圆频率；嗞称为初相位。以f＝ωn/2π表示每秒中振动的周数，称为频率；它的倒数，T=1/f，表示振动一周所需的时间，称为周期。振幅A、频率f(或角频率ωn)、初相位嗞，称为简谐振动三要素。
如图2所示，由线性弹簧联结的集中质量m构成简揩振子。当振动位移自平衡位置算起时，其振动方程为：
塯 +ω厒x＝0，式中
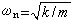，k为弹簧的刚度。上式的通解就是(1)。A和嗞可由t=0时的初始位置x0和初速度凧0决定：
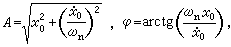但ωn只由系统本身的特征m和k决定，与外加的初始条件无关，故ωn亦称固有频率。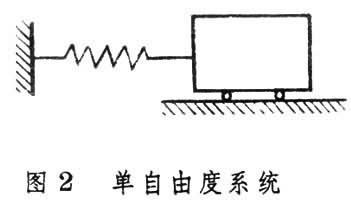
对于简谐振子，其动能
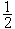m凧2和势能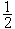kx2之和为一常量，即系统的总机械能守恒。在振动过程中，动能和势能不断相互转化。阻尼振动 存在摩擦和介质阻力或其他能耗，而使振幅不断衰减的振动。对于微振动，速度一般不很大，介质阻力与速度一次方成正比，可写作-c凧，c为阻尼系数。所以具有线性阻尼的单自由度振动方程可写作：
塯＋2β凧＋ω厒x＝0， (2)式中β=c/2m称为阻尼参变量，
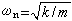。式(2)的通解可写作：
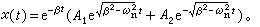(3)依据ωn和β之间的数值关系可分为以下三种情况：①ωn＞β（小阻尼情况） 质点产生衰减振动，其振动方程为：
x(t)=Ae-βtcos(ω1t-嗞)，其振幅按方程A=A0e-βt所示的指数规律随着时间的推移而减小，如图3虚线所示。严格地说，这种振动是非周期性的，不过按式(3)可定义其峰值的频率为：
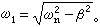eβτ称为减幅率，其中τ为振动周期。减幅率的自然对数δ称为对数减(幅)率；显然，δ＝βτ，式中τ＝2π/ω1。直接通过实验测定δ和τ，利用上式即可求出c。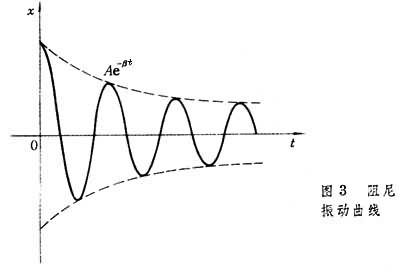
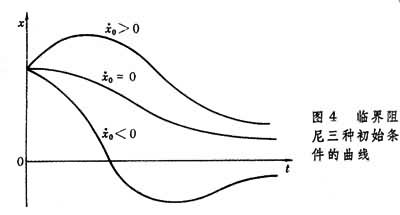
②ωn＝β（临界阻尼情况） 此时式(2)的解可写作：
x(t)=(A1+A2t)e-βt它随初速度凧0的方向又可分为如图4所示的三种非振动情况。
③ωn＜β（大阻尼情况） 式(2)的解如式(3)。这时，系统已不是振动的了。
受迫振动 系统在经常性激励作用下的振动。振动分析主要是考察系统对激励的响应。周期激励是一种典型的经常性激励。由于周期激励总可分解为若干个谐和激励之和，故根据叠加原理，只要求出系统对各个谐和激励的响应，再把它们叠加起来，就可得到系统对周期激励的总响应。 单自由度带阻尼的系统在谐和激励F0sinωt的作用下，运动微分方程可写作：
m塯＋c凧＋kx＝F0sinωt。其响应是两部分的和，一部分是阻尼振动的响应，这部分随时间增大而迅速衰减；另一部分受迫振动的响应可写作：
x＝hsin(ωt-ψ)，式中
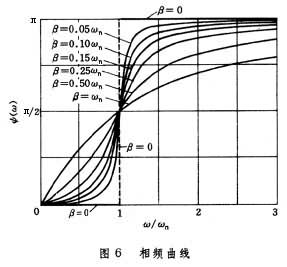
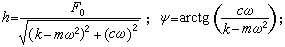h/F0=H(ω)，为定常响应振幅与激励振幅之比，表征幅频特性，或称增益函数；ψ为定常响应和激励的相位差，表征相频特性。它们与激励频率ω的关系见图5和图6。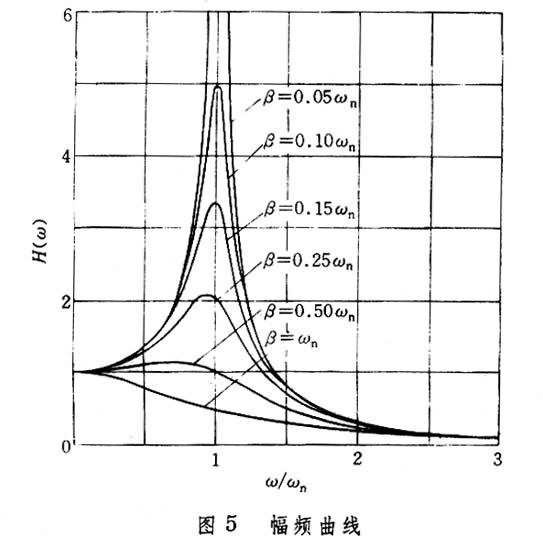
从图5可以看出，在小阻尼情况下，幅频曲线具有单峰；阻尼愈小，峰愈陡；对应于峰顶的频率称为系统的共振频率。在小阻尼情况，共振频率与固有频率差别不大。当激振频率与固有频率接近时，振幅急剧增加，这种现象称为共振(谐振)。在共振时，系统的增益取极大值，即受迫振动最为激烈。故在一般情形下，总是力求避免出现共振，除非某些仪器与设备要利用共振来取得大幅度振动。
从图6可以看出，不论阻尼大小，在ωn处，相位差ψ＝π/2，这一特点可有效地用于共振测量。
除了定常激励外，系统有时还会遇到非定常激励。它大致可以分为两类：一是实发性的冲击作用；二是任意性的持久作用。在非定常激励下，系统的响应也是非定常的。
分析非定常振动的一个有力工具是脉冲响应法。它用系统的单位脉冲输入的瞬态响应描述系统的动态特性。单位脉冲可以用δ函数表示。在工程上，δ函数常定义为：
δ(t)=0，当t厵0，
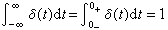，式中0-表示t轴上从左边趋于零的点；0+表示从右边趋于0的点。 系统对应于在 t=0时作用的单位脉冲所产生的响应h(t)，称为脉冲响应函数。假定系统在脉冲作用之前是静止的，则当t＜0时，有h(t)=0。知道系统的脉冲响应函数，就可以求系统对任意输入x(t)的响应。这时，可以把x(t)看作一系列脉冲微元x(τ)dτ的和(图7）。
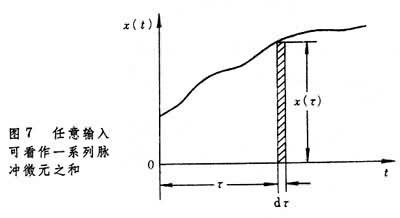x(τ)dτ相当于在t=τ时作用的一个脉冲，系统对应于它的响应为：dy=h(t-τ)x(τ)dτ。基于叠加原理，系统对应于x(t)的总响应为：
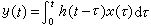。这一积分称为褶积积分或叠加积分。多自由度系统的线性振动 自由度n≥2的线性系统的振动。
图8给出由耦合弹簧联结的两个简谐振子系统。因为它是二自由度系统，所以要用两个独立坐标才能确定其位置。这一系统存在两个固有频率：
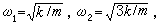每个频率对应一种振动形态。各简谐振子进行同频的谐和振动，同步地通过平衡位置，又同步地到达极端位置，这种振动称为主振动。在对应于ω1的主振动中，有x1=x2；在对应于ω2的主振动中，有x1=-x2。在主振动中各个质量的位移之比保持一个确定的关系，构成一个确定的振型，称为主振型或固有振型。各个主振型之间存在着关于质量与刚度的正交性，它反映各个主振动之间的相互独立性。固有频率与主振型表征多自由度系统所固有的振动特性。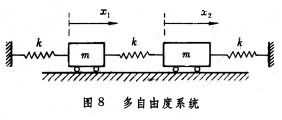
一个n自由度系统有n个固有频率和n个主振型。系统的任何振动形态都可以表成各个主振型的线性组合。因此，在多自由度系统动响应分析中，广泛采用主振型叠加法。这样，系统固有振动特性的测试和分析也就成为系统动态设计的一个常规步骤。
多自由度系统的动态特性也可以用频率特性描述。由于各个输入输出之间都有一个频率特性函数，故构成一个频率特性矩阵。频率特性与主振型之间有确定的关系式。和单自由度系统不同，多自由系统的幅频特性曲线具有多个共振峰。
弹性体振动 上述多自由度系统是弹性体的近似力学模型。弹性体具有无限多个自由度。两者有数量差别而没有本质差别。任何一个弹性体具有无限多个固有频率以及无限多个与之相应的主振型，而且这些主振型之间也存在着关于质量与刚度的正交性。弹性体的任何振动形态也可表示为各主振型的线性叠加。因而对于弹性体的动响应分析，主振型叠加法仍然适用（见弹性体的线性振动）。
以弦的振动为例。设单位长度质量为m的细弦，长l，两端张紧，张力为T。这时，弦的固有频率由下式确定：
f=na/2l (n=1，2，3…)，式中a=(T/m)1/2，是横波沿弦线方向的传播速度。弦的各阶固有频率恰巧为基频a/2l的整数倍。这种整数倍关系导致悦耳的谐音结构。在一般情况下，弹性体各阶固有频率并不存在这种整数倍关系。
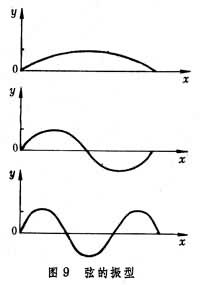
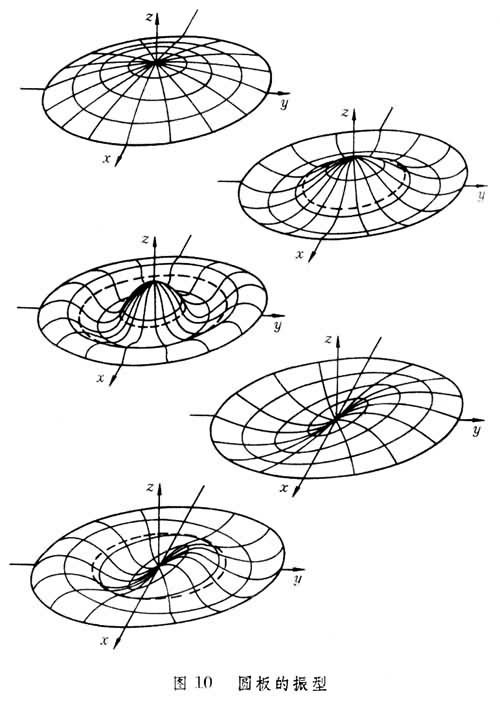
张紧弦的前三阶振型如图9所示，主振型曲线上有一些节点。在主振动中，各节点处不振动。图10给出了周边固支的圆板的几个典型振型，图上有一些由圆和直径构成的节线。
弹性体振动问题的准确提法可归结为偏微分方程的边值问题。但只有在一些最简单的情况下才能找到准确解，因而对于复杂的弹性体振动问题，不得不求助于近似解法。各种近似解法的要旨是变无限为有限，也就是将无限多个自由度系统（连续系统）离散化为有限多个自由度系统（离散系统）。工程分析中广泛采用的离散化方法有两大类：有限元法与模态综合法。
有限元法是将一个复杂结构抽象化为有限个单元并在有限个结点处对接而成的组合结构。每个单元是一个弹性体元件；单元的分布位移用结点位移的插值函数表示；再将各单元的分布参量按一定的格式集中到各个结点上去，由此得出离散系统的力学模型。
模态综合法是将一个复杂结构分解成若干个较为简单的子结构。在弄清各子结构振动特性的基础上，根据对接面上的协调条件将这些子结构合成一总体结构，然后利用各子结构的振动形态得出总体结构的振动形态。
这两种方法既有区别又有联系，可参照使用。模态综合法还可与实验测定有效地结合，构成理论与实验相结合的、关于大型系统振动问题的分析方法。（见振动，非线性振动）
参考书目
铁摩辛柯等著，胡人礼译：《工程中的振动问题》，科学出版社， 北京， 1981。（S. Timoshenko， et al.，Vibration Problems in Engineering， 4th ed.，John Wiley & Sons， New York， 1974.)
W. T. Thomson， Theory of Vibration with Application，2nd ed.， Prentice-Hall， Englewood Cliffs，New Jersey， 1981.
L. Meirovitch， Elements of Vibration Analysis， McGraw-Hill， New York，1975.