量子力学的微扰论(卷名：物理学)
perturbation theory in quantum mechanics
解薛定谔方程的一种常用的近似方法。一个量子体系，如果总哈密顿量的各部分具有不同的数量级，又对于它精确求解薛定谔方程有困难，但对于哈密顿量的主要部分可以精确求解，便可先略去次要部分，对简化的薛定谔方程求出精确解；再从简化问题的精确解出发，把略去的次要部分对系统的影响逐级考虑进去，从而得出逐步接近于原来问题精确解的各级近似解。这种方法称为微扰论。
对于哈密顿量H不显含时间的体系，其不含时间的薛定谔方程为
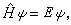(1)如果 
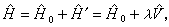(2)其中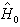
为未受微扰的哈密顿算符(主要部分)，
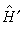为微扰项（次要部分），
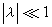，λ是用来表示微扰强度特征的小参数。若
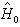的本征方程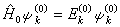
(3)已解出，
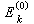是未受微扰体系的能量，
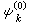是与之相应的波函数。当考虑到
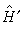的作用后，体系的能量与波函数将发生微小变化，此变化依赖于参数λ，于是体系能量和波函数可按λ的幂次作微扰展开
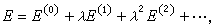(4)
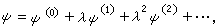(5)当λ＝0时，显然有
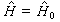，且E＝E(0)，ψ＝ψ(0)。将式(4)、(5)代入式(1)，按λ幂次得到一系列确定E(0)、ψ(0)，E(1)、ψ(1)，…的等式。实际上λ的幂次标志着数量级的大小，依次地，E(0)、ψ(0)分别为E、ψ的零级近似能量和波函数，它们已由式(3)解出，由零级近似解以及
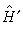，可进一步得到能量和波函数一级修正值E(1)和ψ(1)，也就是得到了E、ψ的一级近似解E(0)+ E(1)、ψ(0)+ψ(1)，以此类推，可逐级求出高级近似解。计算表明，准确到n(n=1，2，…)级近似的能量等于
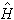对于归一化的第n-1级近似波函数下的平均值。以上是定态微扰论的物理思想。当体系的哈密顿量显含时间时，体系无确定能量，只要求波函数的近似解，处理问题的基本思想与定态微扰论相同，所不同的是将解不含时间的薛定谔方程改为解含时间的薛定谔方程。这种微扰论是含时间的微扰论。微扰论的具体形式虽是多种多样的，但都体现了这样一个特点：微扰项对未受微扰体系的解影响很小，可以通过逐级近似求解。
利用微扰论处理实际问题时，如果
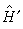较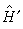小得多，使得微扰展开式收敛得较快，就只要计算一、二级微扰便可得到较为满意的结果。量子力学中的微扰论广泛地应用于原子和分子物理学中，它常与量子力学的变分法等近似方法结合起来使用。