金属光学(卷名：物理学)
optics of metals
研究金属的光学性质及其与金属物质结构关系的学科。金属最显著的光学特性是反射高，吸收强，要薄到300～400埃才开始透光。这同金属具有良好的导电性有关。
发展简史 金属光学的发展历史可追溯到19世纪中叶提倡光的弹性以太理论时期，透明媒质的菲涅耳公式（见光在分界面上的折射和反射）那时已建立起来。人们开始注意研究金属的反射性能，并测量了它的折射率和吸收系数。但是金属光学的重大进展是在麦克斯韦光的电磁理论问世之后。特别是20世纪初，P.K.L.德鲁德将经典电子论应用于金属媒质，使金属的光学常数同其自由电子参量建立起关系。但理论和实验不尽一致。此后的研究工作主要在实验方面。例如，在高真空中制备样品，提高光学量的测量准确度，进行低温测量以观测温度效应等等。随着固体物理学的发展，金属光学到50年代便完全纳入固体物理学的研究领域，以量子理论为理论基础了。但由于历史原因，一些光学教本现仍辟有“金属光学”章节，主要讨论金属的宏观光学性质及其经典色散理论。本条介绍亦限于此，其他可参见固体的能带等。
学科内容 下面主要讨论金属的光学性质和根据经典电子理论（见金属电子论）来分析金属的光学性质。
吸收媒质的复折射率 光波是电磁波，在金属中传播时会因焦耳热损耗而衰减，造成金属媒质对光的吸收。吸收媒质中的单色平面波通常可表成
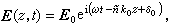式中=n-iⅹ是吸收媒质的复折射率，其中n 是普通的折射率，决定波的相速，而ⅹ是消光系数，决定波的衰减。亦有文献定义=n(1-ix)。复折射率的引入，使透明媒质情况的各项公式（如折射定律、菲涅耳公式等等）在吸收情况下形式仍然有效（见光的吸收）。金属对光的反射 根据菲涅耳公式，光在界面正入射时空气-金属界面的振幅反射系数为
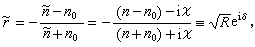式中n0是空气折射率，δ是反射相变，R为反射率。由最后等式可以得到
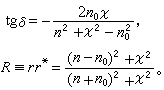样品足够厚时，进入金属界面的光全部被吸收而化为热。吸收率
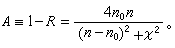ⅹ越大，习惯上说媒质吸收越强。其含义应理解为进入媒质的波衰减得越快。实际上，吸收率A随ⅹ的增大而减小。斜入射时，同样可根据菲涅耳公式来计算有关各量。这时s分量（振动垂直于入射面）和p分量（振动平行于入射面）的反射相变不等，因而线偏振光经金属界面反射一般成为椭圆偏振光。测出此椭圆的方位角和轴长之比，可通过相应公式计算出n和ⅹ。这是测定金属光学常数的一种重要方法。
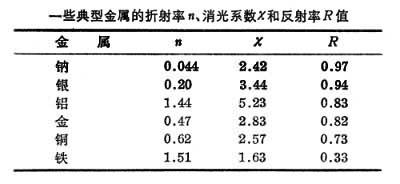
下表列出一些典型金属的n、ⅹ 和R值（λ0=5893埃）。
吸收系数、透入深度和趋肤效应 光在金属内的强度衰减规律是
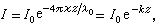式中λ0为真空中波长，
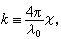称为吸收系数。ⅹ＝1时，k≈2.5×105厘米-1（设λ0≈0.5微米）。这个量级的k值代表强吸收。距离 
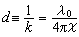称为透入深度。取上列k值时，d≈4×10-6厘米＝400埃。所以，在金属的强吸收区，光波仅能进入其界面内极薄一层地区。按照交流电输送技术用语，人们亦称此为趋肤效应，d/2则称为趋肤深度。n、ⅹ的色散和温度效应 金属的光学常数n、ⅹ随波长改变，即二者有色散。作为示例，图1给出0.2～10.0微米波段Ag的n、ⅹ色散曲线。大体上说，从红外往长波，金属的n、ⅹ 随λ0单调增大。数量级可从10增加到102，反射自然很高；从可见往短波，到200nm以下，曲线n(λ0)和ⅹ(λ0)具有一定结构。按照固体理论，红外区以远是金属中传导电子（经典自由电子）同光相互作用起主导的波段，即色散机制来自导带电子的带内运动；而紫外一端，光子能量较高，金属电子的带间跃迁开始参与作用。
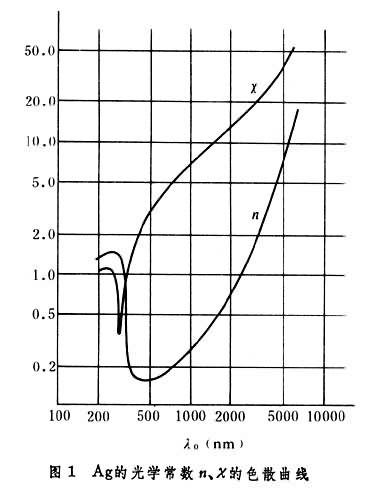
碱金属(Li，Na，K…)和Ag，Al，Ti等金属的色散曲线还存在一个临界波长λc:λ0＞λc时，吸收强，反射高；λ0≤λc时，吸收弱，透射随λ0的减小而显著增大。Al，Ti等的λc 在500～1000埃范围，碱金属的 λc在2000～4000埃范围， Ag的λc≈3300埃。这种透明区的产生机制比较复杂。
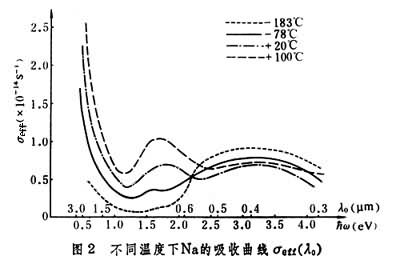
金属光学常数n、ⅹ又是温度T的函数。图2 给出Na的吸收(Na)对温度的依赖关系。在自由电子吸收区（长波），Na随温度T增大；在带间跃迁吸收区（短波），温度效应可因吸收带而异。
复介电常数 金属通常由无规取向的细小晶粒组成，宏观上呈现出各向同性。这时金属的电磁性质可由三个常数来表征：介电常数ε，电导率N，磁导率μ。在超高频以上范围（ω>1010赫），金属的μ＝1，故可不考虑其磁性。
根据麦克斯韦方程组，在单色场下可引进一个复介电常数
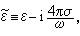使得媒质情况的各项结果在形式上对金属仍然有效。埣和复折射率满足关系式
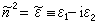，其中实部ε1和虚部ε2分别表征金属的总极化和总吸收。由于色散效应，ε(ω)和N(ω)本身也可成为复量。前者意味着进入带间跃迁吸收区，后者则是由于传导电子的弛豫效应。上式导致
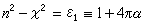， (1)
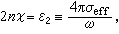(2)式中α为总极化率，Na为有效电导率。α和Na可通过理论计算用金属的原子、电子的参量来表出。所以关系式(1)、(2)是金属光学理论和实验的重要桥梁。 自由电子模型 金属光学常数的色散特性，主要是长波部分，可用经典电子模型来说明。按照这一模型，金属中存在大量脱离原子束缚的自由电子，金属的导电性、导热性等等均归于其自由电子的行为。在静电场下，金属中的自由电子获得附加定向速度，形成传导电流。严格计算需借助统计理论。简单处理可采用模型电子，从其运动方程
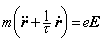导出电导率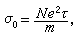
式中N是单位体积内自由电子数；e是电子电荷;m是电子质量（固体物理中换作传导电子的有效质量m*）;τ是弛豫时间，粗略地讲就是自由电子在运动中经受碰撞相隔的平均时间，其典型数量级是10-14，秒。在时谐电场下，金属的电导率
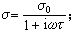传导电流不仅幅值下降，而且同电场发生位相差。这在光波周期接近甚至大于弛豫时间（即ωτ塼1）时才为明显，故称弛豫效应。将上式代入
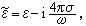不考虑束缚电子的吸收（ε为实数），可得到德鲁德公式
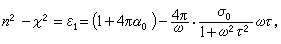(3)
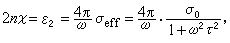(4)式中α0为自由电子以外粒子对极化贡献之和。式(3)、(4)描写金属自由电子弛豫效应所导致的n、ⅹ色散。
当ωτ
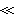1时，Na=N0，ε1=1+4πα0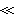ε2，这时可得到经典趋肤深度
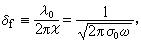吸收率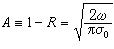 
称鲁宾斯－哈根(Rubens-Hagen)关系。当ωτ
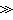1时，弛豫效应强烈，由式(3)可得到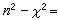
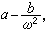其中a=1+4πα0，
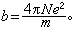实验证明n2-ⅹ2和
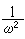成线性关系，并由此求得α0和N/m。弛豫效应很强时，
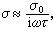传导电流和光场的位相差约90°，自由电子的极化作用远大于吸收，金属类似介质。如果令τ→∞，则吸收2nⅹ＝ε2→0，而
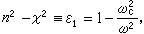式中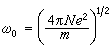
(α0设为零)。这样，当ω＜ωc时，ε1＜0，因而n=0，
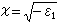R →1；当ω＞ωc时，ε1＞0，因而
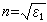，ⅹ＝0。所以频率ωc是τ值有限时金属从高反射过渡到弱吸收的临界标志，相应波长就是临界波长λc。ω＝ωc时，ε1＝0。这正好是无限大理想金属中等离子体振荡的频率条件。所以金属的临界频率ωc就等于金属的等离子体频率。
反常趋肤效应 电磁场的趋肤深度δf与金属的电导率
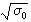成反比，而N0与温度T有关。降低金属温度T，可减小δf。当δf接近甚至小于金属中传导电子的平均自由程l时，就必须考虑电磁场的空间衰减对电子运动的影响。这时通常的欧姆定律j＝N0E 和以此为基础的经典理论均告失效，结果产生反常趋肤效应。这主要是一个高频和低温效应，其典型现象是金属吸收率A 这时与N0(T)无关而为一常数。显然这时传导电子在金属内表面上的散射机理和能量损失决定吸收率A。1940年，由于雷达研究的需要，A.B.皮帕德在测量Sn的高频低温电导率时发现了这一效应。随后有人给出了详细的理论分析。
参考书目
M.玻恩、E.沃耳夫著，黄乐天等译：《光学原理》，下册，科学出版社，北京，1981。(M.Born and E. Wolf，Principles of Optics，5th ed.， Pergamon Press， Oxford， 1975.)
F.Abeles，ed.，Optical Properties and Electronic Structure of Metals and Alloys，North-Holland，Amsterdam，1966.