统计量(卷名：数学)
statistic
样本的已知函数；其作用是把样本中有关总体的信息汇集起来；是数理统计学中一个重要的基本概念。统计量依赖且只依赖于样本x1，x2，…xn;它不含总体分布的任何未知参数。从样本推断总体（见统计推断）通常是通过统计量进行的。例如x1，x2，…，xn是从正态总体N(μ ，1)（见正态分布）中抽出的简单随机样本，其中均值（见数学期望）μ是未知的，为了对μ作出推断，计算样本均值
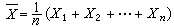。可以证明，在一定意义下，塣包含样本中有关μ的全部信息，因而能对μ作出良好的推断。这里塣只依赖于样本x1，x2，…，xn，是一个统计量。常用统计量 有下面几种。
样本矩 设x1，x2，…，xn是一个大小为n的样本，对自然数 k，分别称
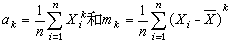为k阶样本原点矩和k阶样本中心矩， 统称为样本矩。许多最常用的统计量，都可由样本矩构造。例如，样本均值
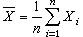（即α1）和样本方差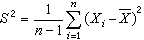 
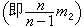是常用的两个统计量，前者反映总体中心位置的信息，后者反映总体分散情况。还有其他常用的统计量，如样本标准差
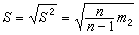，样本变异系数S/塣，样本偏度
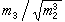，样本峰度
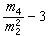等都是样本矩的函数。若(x1，Y1)，(x2，Y2)，…，(xn，Yn)是从二维总体(x，Y)抽出的简单样本，则样本协方差
·
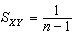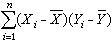及样本相关系数
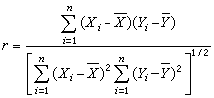也是常用的统计量，r可用于推断x和Y的相关性。次序统计量 把样本X1，x2，…，xn由小到大排列，得到
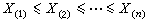，称之为样本x1，x2，…，xn的次序统计量。其中最小次序统计量 x(1)最大次序统计量x(n)称为极值，在那些如年枯水量、年最大地震级数、材料的断裂强度等的统计问题中很有用。还有一些由次序统计量派生出来的有用的统计量，如：样本中位数 
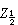是总体分布中心位置的一种度量，若样本大小 n为奇数，
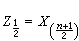，若n为偶数，
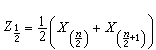，它容易计算且有良好的稳健性。样本p分位数Zp(0<p<1)及极差x(n)-x(1)也是重要的统计量。其中Zp当
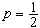时即为中位数，而当
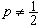时，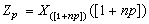
表示不超过1+np的最大整数）。样本分位数的一个重要应用是构造连续总体分布的非参数性容忍区间（见区间估计）。U统计量 这是W.霍夫丁于1948年引进的，它在非参数统计中有广泛的应用。其定义是:设x1，x2，…，xn，为简单样本，m为不超过n的自然数，
为m元对称函数，则称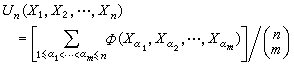
为样本x1，x2，…，xn的以
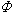为核的U统计量。样本均值和样本方差都是它的特例。从霍夫丁开始，这种统计量的大样本性质得到了深入的研究，主要应用于构造非参数性的量的一致最小方差无偏估计（见点估计），并在这种估计的基础上检验非参数性总体中的有关假设。秩统计量 把样本 X1，X2，…，Xn 按大小排列为
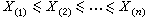，若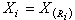
则称Ri为xi的秩，全部n个秩R1，R2，…，Rn构成秩统计量，它的取值总是1，2，…，n的某个排列。秩统计量是非参数统计的一个主要工具。还有一些统计量是因其与一定的统计方法的联系而引进的。如假设检验中的似然比原则所导致的似然比统计量，K.皮尔森的拟合优度（见假设检验）准则所导致的ⅹ2统计量，线性统计模型中的最小二乘法所导致的一系列线性与二次型统计量，等等。
充分性与完全性 统计量是由样本加工而成的， 在用统计量代替样本作统计推断时，样本中所含的信息可能有所损失，如果在将样本加工为统计量时，信息毫无损失，则称此统计量为充分统计量。例如，从一大批产品中依次抽出n个，若第i次抽出的是合格品，则xi=0，否则xi=1(i=1，2，…，n)。总体分布取决于整批产品的废品率p，可以证明:统计量
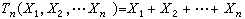，即样本中的废品个数，包含了(x1，x2，…，xn)中有关p的全部信息，是一个充分统计量。若取m<n，令Tm(x1，
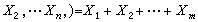，则Tm仍是一个统计量，不过不是充分的。 充分性是数理统计的一个重要基本概念，它是R.A.费希尔在1925年引进的，费希尔提出，并由J.奈曼和P.R.哈尔莫斯在1949年严格证明了一个判定统计量充分性的方法，叫因子分解定理。这个定理适用面广且应用方便，利用它可以验证很多常见统计量的充分性。例如，若正态总体有已知方差，则样本均值塣是充分统计量。若正态总体的均值、方差都未知，则样本均值和样本方差S2合起来构成充分统计量(塣，S2)。一个统计量是否充分，与总体分布有密切关系。
将样本加工成统计量要求越简单越好。简单的程度的大小，主要用统计量的维数来衡量。简单地讲，若统计量T2是由统计量T1加工而来(即T2是T1的函数)，则T2比T1简单。在此意义上，最简单的充分统计量叫极小充分统计量。这是E.L.莱曼和H.谢菲于1950年提出的。前例中的充分统计量都有极小性。在任何情况下，样本x1，x2，…，xn本身就是一个充分统计量，但一般不是极小的。
关于统计量的另一个重要的基本概念是完全性。设T为一统计量，θ为总体分布参数，若对θ的任意函数g(θ)，基于T的无偏估计至多只有一个（以概率1相等的两个估计量视为相同），则称T为完全的。
抽样分布 统计量的分布叫抽样分布。它与样本分布不同，后者是指样本x1，x2，…，xn的联合分布。
统计量的性质以及使用某一统计量作推断的优良性，取决于其分布。所以抽样分布的研究是数理统计中的重要课题。寻找统计量的精确的抽样分布，属于所谓的小样本理论（见大样本统计）的范围，但是只在总体分布为正态时取得比较系统的结果。对一维正态总体，有三个重要的抽样分布，即ⅹ2分布、t分布和F分布。
ⅹ2分布 设随机变量x1，x2，…，xn是相互独立且服从标准正态分布N(0，1)，则随机变量
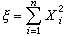的分布称为自由度为n的ⅹ2分布(其密度函数及下文的t分布、F分布的密度函数表达式均见概率分布)。这个分布是 F.赫尔梅特于1875年在研究正态总体的样本方差时得到的。若x1，x2，…，xn是抽自正态总体N(μ，σ2)的简单样本，则变量
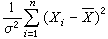服从自由度为n-1的ⅹ2分布。若x1，x2，…，xn服从的不是标准正态分布，而依次是正态分布N(μi，1)(i=1，2，…，n)，则
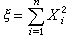的分布称为非中心ⅹ2分布，
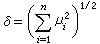称为非中心参数。 当δ＝0时即前面所定义的ⅹ2分布。为此，有时也称它为中心ⅹ2分布。中心与非中心的ⅹ2分布在正态线性模型误差方差的估计理论中，在正态总体方差的检验问题中(见假设检验)，以及一般地在正态变量的二次型理论中都有重要的应用。t分布 设随机变量ξ，η独立，且分别服从正态分布N(δ，1)及自由度n的中心ⅹ2分布，则变量
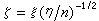的分布称为自由度n、非中心参数δ的非中心t分布；当δ＝0时称为中心t分布。若x1，x2，…，xn是从正态总体N（μ ，σ2）中抽出的简单样本，以塣记样本均值，以
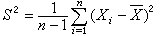记样本方差，则
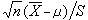服从自由度n-1的t分布。这个结果是英国统计学家W.S.戈塞特(又译哥色特，笔名“学生”)于 1908年提出的。t分布在有关正态总体均值的估计和检验问题中，在正态线性统计模型对可估函数的推断问题中有重要意义，t分布的出现开始了数理统计的小样本理论的发展。F分布 是 R.A.费希尔在20世纪20年代提出的。设随机变量ξ，η独立，ξ服从自由度m、非中心参数δ的非中心ⅹ2分布，η服从自由度n的中心ⅹ2分布，则
的分布称为自由度(m，n)、非中心参数δ的非中心F分布，当δ=0时称为中心F 分布。若x1，x2，…，xm和Y1，Y2，…，Yn分别是从正态总体N(μ ，σ2)和N(v，σ2)，中抽出的独立简单样本，以S娝和S娤分别记为诸xi和诸Yi的样本方差，则方差比统计量S娝/S娤服从自由度(m-1，n-1)的中心F分布。中心和非中心的 F分布在方差分析理论中有重要应用。多维正态总体的重要的抽样分布有维夏特分布和霍特林的T2分布（见多元统计分析）。
一个统计量若服从某分布，常以该分布的名字命名该统计量，如ⅹ2统计量、F统计量、T2统计量等。
由于寻找精确的抽样分布有困难，统计学者转而研究当样本大小 n→∞时统计量的渐近分布(即极限分布)，这种研究是数理统计大样本理论的基础性工作。已经有很多重要的统计方法，就是基于这种工作而提出的。像K.皮尔森关于拟合优度统计量的极限分布是ⅹ2分布的著名结果(1900)就是一个有代表性的例子。
参考书目
复旦大学编：《概率论》（第2册，数理统计），人民教育出版社，北京，1979。
费史著，王福保译：《概率论及数理统计》，上海科学技术出版社，上海，1962。(M.Fisz，Wahrscheinlichkei-tsrechnung und MatheMatische Statistik，VEB Deu-tscher Verlag der Wissenschaften，Berlin， 1958.)
陈希孺著:《数理统计引论》，科学出版社，北京，1981。