鞅(卷名：数学)
martingale
一类特殊的随机过程，起源于对公平赌博过程的数学描述。martingale一词的原义之一，是表示一种赌输一局后加倍下注的策略，此处则是借用这个词的另一译义“鞅”(马颔缰的古称)作为这类随机过程的名称。设T是实数轴R的一个子集，x＝{x(t)，t∈T}是概率空间(Ω，F，p)上的随机过程，E|x(t)|<∞，又设{Ft，t∈T}是一族随t增大的F的子σ域（见概率），而且x(t)是Ft可测的（即对任何实数x，事件{x(t)≤x}∈Ft），Ft可以理解为到时刻t为止通过观测可能获得的全部信息。若对任何s，t∈T，s<t，x(t)关于Fs的条件期望就等于x(s)，即E(x(t)｜Fs=x(s)，则称x为(Ft)鞅，或简称为鞅。如果形象地把 x(t)看作一场赌博中某个局中人在时刻t的本金，Fs看作他到时刻s为止积累起来的经验，那么鞅的性质就是表明，不论他在时刻s以后的赌博中如何利用已得的经验Fs，他所能期望于未来时刻t的本金仍然只能是x(s)，这正是“公平性”的体现。x的指标集T通常取作非负整数集N ={0，1，2，…}，或正实半轴R +=[0，∞)，前者称为离散时间鞅，后者称为连续时间鞅。近年来，T为一般半序空间的鞅论也有了较大的进展。均值为零的独立随机变量序列的部分和，布朗运动，均值为零的独立增量过程（例如泊松过程减去其均值函数），都是鞅的典型例子。
按照最小均方误差的准则，对于一个方差有限的随机变量ξ，如果已经观测到Fs，ξ的最佳估计就是它关于Fs的条件期望E(ξ｜Fs)。因此，对于一个方差有限的鞅，“现在状态”x(s)本身就是对“未来状态”x(t)的最佳预测。它的这一特点，对鞅论广泛应用于现代估计理论，特别是非线性估计理论，起着重要的作用。
P.莱维等人早在1935年就发表了一些孕育着鞅论的工作。1939年，J.维莱首次采用了鞅这个名称。但对鞅进行系统研究并使之成为随机过程论的一个重要分支的，则应归功于J.L.杜布。鞅论的一些基本定理和方法已经日益成为各类随机过程研究的有力工具。
上鞅与下鞅 如果在上述鞅的定义中分别用不等式E(x(t)｜Fs≤x(s)，E(x(t)｜Fs≥x(s)来代替等式（其中s<t），那么满足前一性质的x称为上鞅，满足后一性质的 x称为下鞅。它们都是描述有偏向、不公平的赌博过程的，上鞅是不利于局中人的模型，而下鞅性则表示有利于局中人。
停止定理 有时，不仅需在固定时刻t∈T，而且还要在另一随机现象发生的时刻τ来考虑过程x。这另一随机现象在时刻t以前发生这件事必须是到t为止能够观测到的事件，这就意味着{τ≤t}∈Fi，因此τ是一个停时(见随机过程)。用Fτ表示到τ为止通过观测所能了解的全部事件构成的子
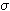域，这种事件B应具有性质：对任何t∈T，B∩{τ≤t}∈Ft。著名的杜布停止定理指出:如果x是(Ft)鞅，那么对于有先后次序的一对有界停时λ≤τ，x(τ)关于Fλ的条件期望就是x(λ)，即
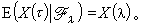上鞅和下鞅也有相应的结果，如对下鞅有E(x(τ)｜F*lambda;)≥x(λ)。收敛定理 对离散时间鞅{xn，n∈N}，如果它具有一致可积性，即对概率充分小的事件 B，xn在 B上的积分
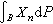可以对n一致地任意小，而且{E｜xn｜，n∈N}有界，那么当n趋于∞时，xn以概率1收敛于一个可积的随机变量x∞。这时由于E(x∞|Fτ)=xτ对一切停时τ成立，从而停止定理中关于停时λ、τ有界性的条件可以取消。对连续时间鞅，同样的事实也成立。进一步，只要在概率为零的事件上适当改变随机变量x(t)的值，就可以使得鞅x在每一时刻 t处的左、右极限都以概率1存在。通常还假定{Ft，t∈R+}是右连续的，即
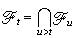，这时可使鞅具有右连续的样本函数。对上鞅和下鞅，若均值函数Ex(t)右连续，也有类似的结果。局部鞅 鞅 X在任一停时 τ处停止得到的随机过程
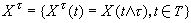还是鞅，其中
。有些随机过程x，虽然它本身未必是鞅，但可以使它在适当停时处停止所得到的随机过程成为鞅。如果能够找到上升趋于∞的停时序列{τn，n∈N}使得x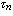
都是鞅，就称x为局部鞅。这是鞅的一种重要推广。上鞅分解定理 1953年，杜布就时间离散的情形证明了每一上鞅{xn，n∈N}都可以表成一个鞅{Mn，n∈N}和一个适应增过程{An，n∈N}之差xn=Mn-An，这里“适应”是指An为Fn可测。“增”则指对任何一对正整数n≤m，An≤Am。由于这一结果简明有用，他同时还提出了对时间连续的情形是否有相应结果的问题。1962～1963年，P.A.迈耶解决了杜布提出的上述问题，即著名的杜布-迈耶上鞅分解定理：右连续上鞅x={x(t)，t∈R +}可表示成一个右连续的一致可积鞅M和一个适应的可积增过程A之差x=M-A，其充分必要条件是随机变量族｛x(τ)，τ取遍一切有界停时｝一致可积。这里，增过程A“可积”是指{EA(t)，t∈R+}有界。满足“{x(τ)}一致可积”这一条件的上鞅也称为“类(D)上鞅”。
如果进一步要求增过程A＝{A(t)，t∈R+}是可料的，而且初值A(0)呏0，则类(D)上鞅的分解x=M-A还是惟一的。
半鞅 从能够进行随机微积分运算和求解随机微分方程这个角度来看，除了鞅以外，还有一类样本函数在任一有限区间上为有界变差的随机过程（它可以表为两个增过程之差）。半鞅就是把这两类过程结合在一起所形成的一类十分广泛而又能够对之进行随机积分等运算的随机过程，即把半鞅定义为一个局部鞅M和一个适应的右连续有界变差过程A之和:x={x(t)=x(0)+M(t)+A(t)，t∈R +}。由杜布-迈耶上鞅分解定理可以证明，上鞅和下鞅都是半鞅。